The 27th International Conference on Atomic Physics

17 Jul 2022, 14:00 → 22 Jul 2022, 14:00 America/Toronto

Koerner Hall (Royal Conservatory of Music, Toronto)

Michal Bajcsy (University of Waterloo), Gordon Drake (University of Windsor), Joseph H. Thywissen (University of Toronto)

The 27th International Conference on Atomic Physics

Registration is open for the 27th International Conference on Atomic Physics (ICAP 2022), which will be held in-person from 17 to 22 July, 2022, in Toronto, Canada. We also offer an online attendance option for those who cannot attend in person due to logistical or health constraints. The meeting features invited plenary presentations and contributed poster presentations on cutting-edge research in the field of atomic, molecular, and optical physics.

Already at the meeting? See our new web site! A program booklet that includes an overview schedule of the meeting is now available, as well as a poster schedule and first draft of the ICAP 2022 proceedings. 

Key dates for ICAP-27 are as follows:

• 22 February 2022: Registration opens
• 7 March 2022: Hot Topics speaker nomination deadline
• 31 March 2022: Invited Hot Topics speakers announced
• 4 April 2022: Travel support and student support request deadline
• 15 April 2022: Visa application (suggested submission date)
• 15 May 2022: ICAP Summer School application deadline
• 20 May 2022: Early-bird registration deadline
• 25 May 2022: Registration opens for virtual participation in ICAP
• 10 June 2022: Poster abstract submission deadline
• 15 June 2022: Refund request deadline
• 30 June 2022: Registration deadline for poster presenters
• 6 July 2022: Standard-rate registration ends. 
• 7-22 July 2022: Late/on-site Registration is now available
• Sunday 17 July, 2pm-7pm: Welcome! Stop by the RCM to pick up your badge
• Sunday 17 July: Welcome Reception, 5pm-7pm
• Monday 18 July: Scientific program starts at 8:40am
• Friday 22 July: Scientific program ends at 12:20pm. Farewell reception 12:30pm - 2:00pm. 

ICAP 2022 Proceedings.pdf

ICAP 2022 Programme.pdf

Poster Locations.pdf

Accompanying Persons and Tourism Information Toronto Tourism website

Sunday 17 July

14:00 → 19:00 Registration / Info Desk Open

Registration and Information Desk Open

17:00 → 19:00 Exhibitors: Welcome reception and exhibiting show opening

Exhibitors and vendors available

Monday 18 July

07:30 → 08:45 Exhibitors: Exhibitor Show Hours 7:30a-5:30p

Exhibitors and vendors available

07:30 → 08:45 Registration / Info Desk open 7:30am-5:30pm

08:45 → 10:30 Plenary session

10:30 → 11:00 Coffee Break

11:10 → 12:20 Plenary session

14:00 → 15:10 Plenary session

15:10 → 15:40 Break

15:50 → 17:00 Plenary session

17:00 → 18:30 Poster session: Monday

17:00 A mobile impurity strongly driven in a Fermi sea

Experimental progress with ultracold atoms has allowed the study of many-body systems far from thermal equilibrium in accessible timescales when compared with solid state systems [1–5]. Moreover, atomic gases offer unique advantages for the control of many of relevant parameters, like the tuning of interactions and the change of internal state, those that have allowed the experimental realization of the Fermi polaron, a impurity immersed in a Fermi sea with Fermi energy $E_{\mathrm{F}}$ [6–14]. By using radio-frequency (RF) the polarons properties have been measured through linear response and Rabi oscillations when the Rabi frequency of the drive $\Omega_{0} < E_{\mathrm{F}}/\hbar$, although little is known about the dynamics and the relaxation between a non-interacting impurity state and the polaron in the strongly driven regime ($ \Omega_{0}\gg E_{\mathrm{F}}/\hbar $).
Here, we study the non-equilibrium dynamics of impurities immersed in a homogeneous Fermi gas. We drive the internal state of the impurities, between one level that does not interact with the Fermi bath, and one that is strongly interacting with it. By using the two-to-lowest Zeeman states of $^{6}$Li we create the two-level system, in which initially the impurities are in $\left|2\right\rangle$ and interact very weakly with the bath in $\left|3\right\rangle$. The minority is then driven to the third internal state $\left|1\right\rangle$ with a RF field, where this state interacts strongly with the bath. We investigate the dynamics of the minority under different drives, from weak $(\Omega_{0}\ll E_{\mathrm{F}}/\hbar)$ to strong $(\Omega_{0}\gg E_{\mathrm{F}}/\hbar)$. We extract the Rabi frequency renormalized by interactions $\Omega_{\mathrm{R}}$ and the relaxation time $T_{2}$ of the effective magnetization $\mathcal{M}$ (the relative population difference) at the resonance of the dressed two-level system. We observe that the system relaxes towards a steady state characterized by a detuning-dependent magnetization, effectively described by a thermalized two-level system [15]. This scenario can be understood as a dissipative two-level system, which evolves to the thermal equilibrium state via interactions with a fermionic bath [16-18]. We also extract the effective $T_{1}$ and $T_{2}$ times characterizing the decay to the steady-state as well as the energy shift of the resonant frequency of the two-level systems. Additionally, we make the connection of this strongly driven impurity-bath system with the (equilibrium) polaron problem and we find that the resonance of the dressed thermalized two-level system, defined as the energy in which this two-level system is equally populated, matches the energy of the polaron as measured by linear-response spectroscopy.

[1] J. Eisert, M. Friesdorf, and C. Gogolin, Nature Physics 11, 124 (2015).
[2] T. Langen, R. Geiger, and J. Schmiedmayer, Annual Review of Condensed Matter Physics 6, 201 (2015).
[3] N. Navon, A. L. Gaunt, R. P. Smith, and Z. Hadzibabic, Science 347, 167 (2015).
[4] N. Navon, A. L. Gaunt, R. P. Smith, and Z. Hadzibabic, Nature 539, 72 (2016).
[5] J. A. P. Glidden, C. Eigen, L. H. Dogra, T. A. Hilker, R. P. Smith, and Z. Hadzibabic, Nature Physics 17, 457 (2021).
[6] A. Schirotzek, C.-H. Wu, A. Sommer, and M. W. Zwierlein, Phys. Rev. Lett. 102, 230402 (2009).
[7] C. Kohstall, M. Zaccanti, M. Jag, A. Trenkwalder, P. Massignan, G. M. Bruun, F. Schreck, and R. Grimm, Nature 485, 615 (2012).
[8] M. Koschorreck, D. Pertot, E. Vogt, B. Fröhlich, M. Feld, and M. Köhl, Nature 485, 619 (2012).
[9] Y. Zhang, W. Ong, I. Arakelyan, and J. E. Thomas, Phys. Rev. Lett. 108, 235302 (2012).
[10] F. Scazza, G. Valtolina, P. Massignan, A. Recati, A. Amico, A. Burchianti, C. Fort, M. Inguscio, M. Zaccanti, and G. Roati, Phys. Rev. Lett. 118, 083602 (2017).
[11] Z. Yan, P. B. Patel, B. Mukherjee, R. J. Fletcher, J. Struck, and M. W. Zwierlein, Phys. Rev. Lett. 122, 093401 (2019).
[12] N. D. Oppong, L. Riegger, O. Bettermann, M. Höfer, J. Levinsen, M. Parish, I. Bloch, and S. Fölling, Phys. Rev. Lett. 122, 193604 (2019).
[13] N. B. Jørgensen, L. Wacker, K. T. Skalmstang, M. M. Parish, J. Levinsen, R. S. Christensen, G. M. Bruun, and J. J. Arlt, Phys. Rev. Lett. 117, 055302
(2016).
[14] Z. Z. Yan, Y. Ni, C. Robens, and M. W. Zwierlein, Science 368, 190 (2020).
[15] A. J. Leggett, S. Chakravarty, A. T. Dorsey, M. P. A. Fisher, A. Garg, and W. Zwerger, Reviews of Modern Physics 59, 1 (1987).
[16] M. Knap, D. A. Abanin, and E. Demler, Phys. Rev. Lett. 111, 265302 (2013).
[17] H. S. Adlong, W. E. Liu, F. Scazza, M. Zaccanti, N. D. Oppong, S. Fölling, M. M. Parish, and J. Levinsen, Phys. Rev. Lett. 125, 133401 (2020).
[18] T. Wasak, M. Sighinolfi, J. Lang, F. Piazza and A. Recati. https://doi.org/10.48550/arXiv.2205.05941

17:00 An Optical Atomic Clock Based on a Highly Charged Ion

Optical atomic clocks are the most precise and accurate measurement devices ever constructed, reaching fractional systematic uncertainties below one part in $10^{18}$ [1]. Their exceptional performance opens up a wide range of applications in fundamental science and technology. The extreme properties of highly charged ions (HCI) make them highly sensitive probes for tests of fundamental physical theories [2, 3]. Furthermore, these properties make them significantly less sensitive to some of the leading systematic perturbations that affect state-of-the-art optical clocks, making them exciting candidates for next-generation clocks [4, 2]. The technical challenges that hindered the development of such clocks have now all been overcome, starting with their extraction from a hot plasma and sympathetic cooling in a linear Paul trap [5], readout of their internal state via quantum logic spectroscopy [6], and finally the preparation of the HCI in the ground state of motion of the trap [7], which allows levels of measurement accuracy to be reached that were previously limited to singly-charged and neutral atoms. Here, we present the first operation of an atomic clock based on an HCI (Ar$^{13+}$ in our case) and a full evaluation of systematic frequency shifts [8]. The achieved uncertainty is almost eight orders of magnitude lower than any previous frequency measurements using HCI. Measurements of some key atomic parameters confirm the theoretical predictions of the favorable properties of HCIs for use in clocks. The comparison to the $^{171}$Yb$^+$ E3 optical clock [9] places the frequency of this transition among the most accurately measured of all time. Furthermore, by comparing the isotope shift between $^{36}$Ar$^{13+}$ and $^{40}$Ar$^{13+}$ to improved atomic structure calculations, we were able for the first time to resolve the largely unexplored QED nuclear recoil effects. Finally, prospects for 5th force tests based on isotope shift spectroscopy of Ca$^+$/Ca$^{14+}$ isotopes and the high-sensitivity search for a variation of the fine-structure constant using HCI will be presented. This demonstrates the suitability of HCI as references for high-accuracy optical clocks and to probe for physics beyond the standard model.

References
[1] Brewer, S. M. et al., Phys. Rev. Lett. 123, 033201 (2019).
[2] Kozlov, M. G. et al., Rev. Mod. Phys. 90, 045005 (2018).
[3] Safronova, M. S. et al., Rev. Mod. Phys. 90, 025008 (2018).
[4] Schiller, S., Phys. Rev. Lett. 98, 180801 (2007).
[5] Schmöger, L. et al., Science 347, 1233–1236 (2015).
[6] Micke, P. et al., Nature 578, 60–65 (2020).
[7] King, S. A. et al., Phys. Rev. X 11, 041049 (2021).
[8] King, S. A. et al., http://arxiv.org/abs/2205.13053.
[9] Lange, R. et al., Phys. Rev. Lett. 126, 011102 (2021).

17:00 Aquila: a field-programmable atom array on the cloud

Neutral atom arrays, trapped and arranged using optical tweezers and interacting with each other when excited to Rydberg states, constitute a rapidly evolving platform for quantum simulation and quantum computation. QuEra Inc. presents Aquila: a 256-qubit cloud-accessible machine, with a connectivity that is programmable by the user via their arrangement in 2D, enabling the encoding of problems ranging from quantum simulation to combinatorial optimization. A global drive to the Rydberg state is also programmable, lending itself to a variety of protocols ranging from collective gate pulses to adiabatic state preparation. Finally, a programmable pattern of local detunings of the Rydberg drive offers a degree of individual addressability for state preparation and optimization over weighted graphs. The field-programmable nature of the Aquila platform makes it a very versatile platform for NISQ-era applications, as well as a versatile testbed for developments towards a fully-controllable neutral atom quantum computer.

17:00 Can a photon cause atoms to be excited for a negative amount of time? (experimental progress)

If a resonant photon traverses a medium and is transmitted on the far side, does it excite any atoms along the way? Previous work (PRX Quantum 3, 010314) provides evidence that it does. Since this work was limited to measurements using only broadband pulses of light, it cannot distinguish between recent theories that make strikingly different predictions in the case of excitation with narrowband pulses and media with low optical depth. In particular, the weak-value formalism suggests that this excitation time could be negative under such conditions. We present experimental progress to investigate this prediction and aim to fully elucidate the history of resonant photons that are ultimately transmitted through a cold cloud of 85Rb atoms.

17:00 Catalyzation and domain supersolidity in binary dipolar condensates

Luis. A. Peña Ardila
Institut für Theoretische Physik, Leibniz Universität Hannover, Appelstr. 2, 30167 Hannover, Germany

Breakthrough experiments have newly explored the fascinating physics of dipolar quantum droplets and supersolids. The recent realization of dipolar mixtures opens further intriguing possibilities. We show that under rather general conditions, the presence of a second component catalyzes droplet nucleation and supersolidity in an otherwise unmodulated condensate. For miscible mixtures, droplet catalyzation results from the effective modification of the relative dipolar strength, and may occur even for a surprisingly small impurity doping. We show that different ground-states may occur, including the possibility of two coexisting interacting supersolids [1,2].

In addition, we predict the existence of a binary supersolid state in which the two components form a series of alternating domains, producing an immiscible double supersolid. Remarkably, we find that a dipolar component can even induce supersolidity in a nondipolar component. In stark contrast to single-component supersolids, the number of crystal sites is not strictly limited by the condensate populations, and the density is hence substantially lower. Our results are applicable to a wide range of dipole moment combinations, marking an important step towards long-lived bulk-supersolidity [3].

[1] R. N. Bisset, L. A. Peña Ardila, L. Santos. Phys. Rev. Lett. 126, 025301 – 2021
[2] D. Scheiermann, L. A. Peña Ardila, T. Bland, R. N. Bisset, L. Santos. arXiv:2202.08259 – 2022
[3] Thomas Bland, Elena Poli, Luis A. Peña Ardila, Luis Santos, Francesca Ferlaino, Russell N. Bisset. arXiv:2203.11119 – 2022

17:00 Catching a particle inside a barrier

Can one detect a tunneling particle inside of a barrier? Traditional quantum measurement of the position of a tunneling particle inside a barrier transfers significant energy to the particle, precluding observation of a tunneling particle while it is in the ‘forbidden’ region. Instead, one might probe a tunneling particle ‘weakly,’ so as to prevent energy transfer, as envisioned by a weak Larmor measurement, and post-selecting on the particle having been in the probed region of the barrier. We theoretically study how this weak, non-disturbing measurement can become strong upon post-selection and enhance transmission through the barrier. We discover a new timescale corresponding to the duration over which particles in the probed region are significantly disturbed, which is tempting to interpret as the time it takes for particles to escape the probed region undetected. We observe that such measurements may lead to experimentally realizable ‘observationally assisted barrier penetration.’

17:00 Cavity-QED Quantum Simulator of Random Spin Models

My poster will present a cavity QED experiment where we use $^6$Li atoms to perform quantum simulations of random spin models.

The atom-cavity system realizes a spin chain with random transition frequencies coupled to an extended photon mode, with controlled disorder realized by a local light-shift of the excited state of the atoms. We study the competition between the collective many-body physics and the disorder in two regimes: in the near-resonant regime, N spins with random energies are coupled to a bosonic mode [1]. In the dispersive regime, one can adiabatically eliminate the cavity to obtain long-range spin-exchange interactions [2]. The effective Hamiltonian can be rewritten in terms of N spins precessing around an external magnetic field with random inhomogeneities. We measure the magnetic susceptibility of the system as a function of the disorder strength and observe the fragmentation of the collective Dicke excitations into semi-localized grey states.

As an outlook, my poster will discuss possible perspectives on using cavity-mediated interaction in combination with our light-shifting technique for the quantum simulation of holographic matter such as SYK-type models [3].

---

[1] Dubail, Jérôme, et al. "Large random arrowhead matrices: Multifractality, semilocalization, and protected transport in disordered quantum spins coupled to a cavity." Physical Review A 105.2 (2022): 023714.
[2] Muniz, Juan A., et al. "Exploring dynamical phase transitions with cold atoms in an optical cavity." Nature 580.7805 (2020): 602-607.
[3] Trunin, Dmitrii Alekseevich. "Pedagogical introduction to the Sachdev-Ye-Kitaev model and two-dimensional dilaton gravity." Physics-Uspekhi 64.3 (2021): 219.

17:00 Cold Ion-Molecule Reactions Relevant to Astrochemistry

Laboratory measurements of cold ion-molecule collisions help to develop understanding of the dynamics and kinetics of interstellar chemistry. In our linear Paul ion trap, we trap ions at cold temperatures and react them with neutral molecules in an isolated environment. The products and branching ratios of these reactions are measured with high resolution with a time-of-flight mass spectrometer. Recently, we studied two reactions of interstellar importance (C$_{2}$H$_{2}^{+}$ + CH$_{3}$CN, acetonitrile and CCl$^{+}$ + C$_{6}$H$_{6}$, benzene) in this apparatus. Isotopologue substitution and quantum chemical calculations aid in identifying and analyzing the resulting products and branching ratios of these reactions. Both systems are potential pathways for the buildup of cyclic carbocations in the interstellar medium. The CCl$^{+}$ + benzene reaction, in particular, demonstrates potential as a participant in the growth of larger aromatics that occurs in the interstellar medium.

17:00 Collective Radiative Dynamics of an Ensemble of Cold Atoms Coupled to an Optical Waveguide

We experimentally and theoretically investigate collective effects in a one-dimensional array of cold atoms coupled to a single-mode optical nanofiber [1]. Our analysis unveils the microscopic (i.e., atom per atom) dynamics of the system, showing that collective interactions gradually build-up along the atomic chain in the direction of propagation of the excitation light pulses. Our theoretical results are supported by time-resolved measurements of the light transmitted and reflected by the atomic ensemble.
In particular, when the excitation pulse is switched off on a time scale much shorter than the atomic lifetime, a superradiant decay is observed in the forward direction, while no speed-up of the decay rate is measured in the backward direction. For longer time scales, our measurements reveal the evolution of the ensemble from the superradiant state to a set of states that are fully subradiant with respect to the fiber mode [2]. Notably, our theoretical model identifies this phenomenon as a key feature of the time evolution of one-dimensional systems prepared in a timed Dicke state. This complex dynamics can be accurately described with a simple analytical expression.
Our results highlight the unique opportunities offered by nanophotonic cold atom systems for the experimental investigation of collective light-matter interaction.

[1] R. Pennetta et al., “Collective Radiative Dynamics of an Ensemble of Cold Atoms Coupled to an Optical Waveguide”, Phys. Rev. Lett., 128, 073601 (2022)

[2] R. Pennetta et al., “Observation of coherent coupling between super- and subradiant states of an ensemble of cold atoms collectively coupled to a single propagating optical mode”, Phys. Rev. Lett. (accepted)

17:00 Control and Entanglement of Rydberg Atoms near a Nanophotonic Device

Rydberg atom arrays are a promising platform for quantum information and quantum computation. However, they lack a photonic link, such as an optical cavity, which could be used for fast non-destructive readout for error correction or for remote entanglement of distant arrays, thus extending the computational capabilities of the platform. The integration between an optical cavity and Rydberg atoms is challenging due to their large polarizability: noise in the electric field generated by surface charges on a cavity can severely limit coherence times. Here we use a nanoscale photonic crystal cavity attached to a fiber. Due to its small size, the nanocavity is a promising candidate for such a photonic interface for Rydberg atom arrays. We characterize the coherence of single- and two-atom Rydberg states near the PCC suggesting a pathway towards their successful integration.

17:00 Detection of Berezinskii-Kosterlitz-Thouless transition via Generative Adversarial Networks

The detection of phase transitions in quantum many-body systems with lowest possible prior knowledge of their details is among the most rousing goals of the flourishing application of machine-learning techniques to physical questions. Here, we train a Generative Adversarial Network (GAN) with the Entanglement Spectrum of a system bipartition, as extracted by means of Matrix Product States ansätze. We are able to identify gapless-to-gapped phase transitions in different one-dimensional models by looking at the machine inability to reconstruct outsider data with respect to the training set. We foresee that GAN-based methods will become instrumental in anomaly detection schemes applied to the determination of phase-diagrams.

17:00 Developing a high-resolution Doppler broadening spectroscopy for cold positronium

Cooling of positronium (Ps), an electron-positron bound state, leads to important research such as precision measurements of energy intervals or realizing Bose-Einstein condensation. The current coldest limit of Ps, which was achieved by thermalization with cooled solid, is still over 100 K [1]. Laser cooling and other cooling methods are under intense research to give a breakthrough in this field. On this occasion, evaluating the temperature of cold Ps is an important task to be undertaken. Obtaining the Doppler broadening by laser spectroscopy is one of the preferred methods since it allows high-resolution measurements regarding the laser technology of today.
However, since Ps has a short lifetime of 142 ns due to the electron-positron annihilation, it is principally difficult to prepare a large number of Ps at once for observation. Thus, to conduct a high-resolution Doppler broadening spectroscopy, not only should the resolution be high, but also the excitation efficiency by the laser should be kept high enough to realize an observation with a high signal-to-noise ratio. This gives certain requirements to the frequency structure and the power of the probing laser.
To evaluate the required characteristics of the probing laser, we conducted a numerical simulation based on optical Bloch equations under laser fields whose frequency structure was realistically modeled. Based on this evaluation, we have developed a frequency-tunable UV pulsed laser with the characteristics suited for doppler spectroscopy of cold Ps. We will introduce an overview of this laser along with the experimental results to evaluate whether our pulsed laser satisfies the above requirements.

[1] S. Mariazzi, P. Bettotti, and R. S. Brusa, Physical Review Letters 104, 243401 (2010).

17:00 Development of a Deep-ultraviolet Chirped Pulse Laser for Doppler Cooling of Positronium

Positronium (Ps), a bound state of an electron and a positron, is a purely leptonic and anti-particle system. Preparing a cold gas of Ps leads to precision spectroscopy and a realization of Bose-Einstein condensation of exotic atoms. Owing to the nature of the particle-antiparticle pair, Ps has a finite lifetime of 142 ns. Therefore, developing a rapid cooling method is the key to cool Ps effectively.
Laser cooling using the 1S-2P transition is one of the most promising methods for Ps cooling. With laser cooling, Ps atoms at room temperature could ideally be cooled to the photon recoil limit of 0.6 K within one microsecond. The temperature is well below 150 K, achieved by a conventional cooling method via momentum exchange processes with a cold Ps converter[1].
It is well known that laser cooling using continuous-wave lasers can reduce the temperature of a gas of atoms to submillikelvin temperatures[2]. However, because of the finite lifetime and the small mass of Ps, a cooling laser for Ps should be a unique pulsed laser that has a broadband spectrum, a frequency chirp, and a long pulse duration of several hundred nanoseconds[3]. We designed and developed a prototypical cooling laser (Figure 1) that satisfies these requirements. We also numerically simulated its oscillation dynamics and successfully reproduced the measured temporal and spectral structures of the laser[4].

[1] S. Mariazzi, P. Bettotti, and R. S. Brusa, Physical Review Letters 104, 243401 (2010).
[2] W. D. Phillips, Reviews of Mordern Physics 70, 721 (1998).
[3] K. Shu, X. Fan, T. Yamazaki, T. Namba, S. Asai, K. Yoshioka, and M. Kuwata-Gonokami, Journal of Physics B: Atomic, Molecular and Optical Physics 49, 104001 (2016).
[4] K. Yamada, Y. Tajima, T. Murayoshi, X. Fan, A. Ishida, T. Namba, S. Asai, M. Kuwata- Gonokami, E. Chae, K. Shu, and K. Yoshioka, Physical Review Applied 16, 014009 (2021).

17:00 Development towards a hybrid quantum repeater

We describe our progress in developing a proof-of-principle hybrid quantum repeater based on laser-cooled caesium ensembles and a semiconductor quantum dot. The atoms here can be used as a quantum memory or as a non-linear medium whilst the quantum dot can be used as a bright source of entangled photon pairs. The laser cooled atoms are loaded inside a hollow-core fiber to achieve an optical depth $\sim$1000. This has the potential to enable strong interactions with photons emitted by the quantum dot, which have bandwidth of $\sim$1 GHz and can be tuned to match the cesium D$_1$ line. The atoms confined in the hollow-core fiber can be used to store single photons from the quantum dot and to realize single-photon wavelength conversions for quantum key distribution (QKD) via ground-to-satellite or telecom-fiber links.

17:00 Dilute quantum liquid in a K-Rb Bose mixture

Recently, the formation of heteronuclear quantum droplets has been observed in an attractive bosonic mixture of $^{41}$K and $^{41}$Rb. [1], with increased lifetimes with respect to the homonuclear mixture of $^{39}$K. In order to enable fruitful comparison with experiments, we have performed a study of the $^{41}$K and $^{41}$Rb mixture using the diffusion Monte Carlo method and the Density Functional Theory [2].

We have proved that the perturbative Lee-Huang-Yang term for a heterogeneous mixture is valid only near the gas-liquid transition. Based on the equations of state of the bulk mixture, calculated with diffusion Monte Carlo, we present extensions to Lee-Huang-Yang corrected mean-field energy functionals.

Using Density Functional Theory, a systematic comparison between different functionals is performed, focusing on the critical atom number, surface tension, surface width, Tolman length, and compressibility. These results are given as a function of the inter-species interaction strength, within the stability domain of the liquid mixture and for an experimentally relevant range of scattering parameters.

[1] C. D’Errico, A. Burchianti, M. Prevedelli, L. Salasnich,F. Ancilotto, M. Modugno, F. Minardi, and C. Fort, Observation of quantum droplets in a heteronuclear bosonic mixture, Phys. Rev. Research 1, 033155 (2019).

[2] V. Cikojević, E. Poli, F. Ancilotto, L. Vranješ Markić, J. Boronat, Dilute quantum liquid in a K-Rb Bose mixture, Phys. Rev. A, 104, 033319 (2021).

17:00 Dynamic cryogenic radiation shield for sub-$10^{-19}$ blackbody radiation shift uncertainty in optical lattice clocks

The blackbody radiation (BBR) Stark shift currently limits the performance of many atomic frequency standards. It constitutes the largest uncancelled shift and the leading uncertainty in the most accurate optical lattice clocks [1,2]. One attempt to tackle this limitation has been to create a well-characterized BBR environment at room temperature [3]. However, the uncertainty on the atomic polarizability manifested as a dynamic correction to the BBR shift limits this strategy at the $10^{-18}$ fractional frequency level. An alternative approach utilizes a cryogenic radiation shield to reduce the total BBR shift and more importantly the above-mentioned BBR dynamic correction uncertainty [4,5]. However, a lingering challenge is to achieve adequate isolation from the external environment. In these attempts, the leaking room temperature BBR limits the shift evaluation uncertainty at the same $10^{-18}$ fractional frequency level.

Here we report on the design of a mechanically dynamic cryogenic in-vacuum radiation shield that enables controlling the BBR shift uncertainty below the $10^{-19}$ level in optical lattice clocks. While the shield accommodates ample physical and optical access during atomic state preparation, mechanical actuation of its internal structure closes all physical and nearly all optical apertures during spectroscopy. The mechanical actuation encloses the atomic sample from virtually all the 4π steradians of solid angle with highly emissive cryogenic surfaces and blocks the atoms’ direct line of sight to the external environment. Consequently, shifts due to leaking room temperature BBR are suppressed below the $10^{-18}$ level. To verify the homogeneity of the cryogenic environment, the shield accommodates temperature measurement and control of all the cryogenic surfaces with direct-line-of-sight to the atoms to be within $100\ \textrm{mK}$ from a mean temperature of $75\ \textrm{K}$ or lower. The shield also acts as a Faraday shield and employs three mutually orthogonal electrode pairs for evaluation of stray electric fields inducing a DC Stark shift. The highly uniform BBR environment delivered by the shield at cryogenic temperatures and up to room temperature provides a controlled platform for many AMO experiments that investigate and seek to eliminate the perturbative BBR environment on their quantum systems.

[1] McGrew, W. F., et al. "Atomic clock performance enabling geodesy below the centimetre level." Nature 564.7734 (2018): 87-90.
[2] Bothwell, T, et al. "JILA SrI optical lattice clock with uncertainty of 2×10-18." Metrologia 56.6 (2019): 065004.
[3] Beloy, K. et al. “Atomic clock with 1×10-18 room-temperature blackbody Stark uncertainty.” Physical Review Letters 113, (2014).
[4] Ushijima, I., et al. “Cryogenic optical lattice clocks.” Nature Photonics 9, 185–189 (2015).
[5] Schwarz, R. “A cryogenic Strontium lattice clock.” Hannover: Gottfried Wilhelm Leibniz Universität, Diss., 2022, x, 166 S.

17:00 Dynamics following an interaction quench in the BEC-BCS crossover and machine-learning the phase diagram

With a specially designed coil [Rev. Sci. Instrum. 92, 093202 (2021)], we quench the interaction strength of an ultracold cloud of $^6$Li atoms instantaneously, i.e. faster than the Fermi time. In the short time dynamics following the quench we observe first indications of an oscillation in the condensate fraction reminiscent of the Higgs-mode.

The observation was facilitated by a deep neural network trained to determine the amount of superfluidity in the cloud from simple time-of-flight images. This quantity is hidden for conventional fitting techniques, especially under real experimental conditions.
We record a high-resolution phase diagram of the BEC-BCS crossover with the neural network and show that such networks are also able to detect the existance of a phase transition without any additional training input.

17:00 Dynamics in a spin imbalanced gas of Li6

Two-component Fermi gases with imbalanced spin populations feature mismatched Fermi surfaces which can lead to a range of novel behaviours. Here, we produce and study spin-imbalanced Fermi gases following a quench which removes a fraction of the atoms in one spin state, from an initially balanced spin-mixture. We apply this approach to harmonically trapped lithium-6 gases and measure the ensuing dynamics as the atoms approach equilibrium. Furthermore, we present our progress towards studies of the contact parameter in spin-imbalanced Fermi gases using Bragg spectroscopy.

17:00 EDMcubed (Electric Dipole measurement using Molecules in a Matrix): Towards a measurement of the electron electric dipole moment using BaF molecules embedded in a solid Ar matrix

Improved measurements of the electron electric dipole moment (eEDM) will strongly constrain the parameter space of new physics theories. Over the last decade, polar molecules have become established as the most promising systems for eEDM searches, due to the large internal electric fields experienced by an eEDM in these molecules. The sensitivity of eEDM searches is determined by the coherence time available for measuring eEDM-induced electron spin precession, as well as by the total number of molecules available over the course of a measurement. We present our progress in implementing a measurement scheme [1] that will use a large number of barium-monofluoride molecules embedded into a solid argon matrix. The large number of BaF is expected for matrix-isolated BaF molecules is expected to lead to excellent statistical precision, and the method offers an array of reversals and controls for cleanly suppressing systematic effects to a level commensurate with the improved statistical precision.

[1] A. C. Vutha, M. Horbatsch and E. A. Hessels, Phys. Rev. A 98, 032513 (2018).

17:00 Effects of pump pulse length on photon number in quantum dot emission

On-demand sources of non-classical light play an important role in quantum information and metrology [Ref. 1], and semiconductor quantum dot (QD) sources promise high-quality and efficient single and entangled photons [Refs. 1, 2]. At the same time, other states of light have been observed in the QD emission [Refs. 3, 4, 5, 6] as the nature of the emitted light relates with the dynamics of the electronic state of the QD. In particular, when the dot is excited by a pulse of light, charge and/or exciton capture processes within the same pulse cycle can cause multi-photon emission.

Here, we predict and measure – using a photon-number-resolving superconducting-nanowire single photon detector – photon correlations and photon number statistics in light emitted by a QD embedded in a semiconductor nanowire [Ref. 2] excited with non-resonant pulses of different lengths.

We model the excitation and emission process as a Markov chain. This allows one to keep track of the photon number distributions of the involved transitions – such as: exciton (X), bi-exciton (XX) and charged exciton (X- ) – along with their coincidences. An illustration of a model and its estimates are presented in Figure 1. We study the role of different parameters in the model, such as pulse lengths and intensities, to explain the observed experimental results.

^{References:
[ 1 ] R. Trivedi et al. Generation of Non-Classical Light Using Semiconductor Quantum Dots, Adv. Quantum Technol. 2020, 3, 1900007
[ 2 ] M. Reimer, G. Bulgarini, N. Akopian et al. Bright single-photon sources in bottom-up tailored nanowires, Nat Commun. 3, 737 (2012)
[ 3 ] K. Fisher et al. Signatures of two-photon pulses from a quantum two-level system, Nature Physics volume 13, 649–654 (2017)
[ 4 ] E. B. Flagg, et al. Dynamics of Nonclassical Light from a Single Solid-State Quantum Emitter, Phys. Rev. Letters 109, 163601 (2012)
[ 5 ] M. H. Baier et al. Quantum-dot exciton dynamics probed by photon-correlation spectroscopy, Phys. Rev. B. 73, 205321 (2006)
[ 6 ] G. Sallen et al. Exciton dynamics of a single quantum dot embedded in a nanowire, Phys. Rev. B. 80, 085310, (2009)}

17:00 Efficient production of an array of fully-quantum-state-controlled polar molecules

Arrays of ultracold polar molecules exhibit long-range, long-lived dipole-dipole interactions that can be harnessed for the quantum simulation of matter, quantum computation, and precision measurements. Crucial to many of these proposals is the ability to produce adjacent pairs of molecules whose quantum states we can individually control. To that end, we detect vacancies in arrays of individually trapped Na and Cs atoms and use acousto-optic deflectors to rearrange the atoms into a vacant free-region. Each pair of Na and Cs is Raman sideband cooled and merged into the same trap, which we then magnetoassociate at a Feshbach resonance and transfer to the NaCs rovibronic ground state using a two-photon STIRAP sequence. Additionally, we performed spectroscopy of the NaCs $c^3\Sigma$ potential. We identified a 15 MHz wide intermediate state for our STIRAP transfer that is more efficient than a 120 MHz wide state used in our prior work. This efficient production of fully quantum-state-controlled polar molecules in optical tweezers will provide new opportunities for dipole-dipole interaction mediated quantum computation and quantum simulation applications.

17:00 Emergent atom pump in a non-hermitian system

The time evolution of a quantum system can be strongly affected by dissipation. Although this mainly implies that the system relaxes to a steady state, in some cases it can make new phases appear and trigger emergent dynamics. In our experiment, we study a Bose-Einstein Condensate dispersively coupled to a high finesse resonator. The cavity is pumped via the atoms, such that the sum of the coupling beam(s) and the intracavity standing wave gives an optical lattice potential. When the dissipation and the coherent timescales are comparable, we find a regime of persistent oscillations where the cavity field does not reach a steady state. In this regime the atoms experience an optical lattice that periodically deforms itself, even without providing an external time dependent drive. Eventually, the dynamic lattice triggers a pumping mechanism. We show complementary measurements of the light field dynamics and of the particle transport, proving the connection between the emergent non-stationarity and the atomic pump.

https://arxiv.org/abs/2112.11502

17:00 Emergent Spin Dynamics in a Superradiant Quantum Gas: From dynamical tunnelling to atomic mode parametric amplifiers

Dynamic transients are a natural ingredient of out-of-equilibrium quantum systems. One paradigmatic example is Dicke superradiance, describing the collectively enhanced population inversion of an ensemble of two-level atoms coupled to a single mode of the electromagnetic field.

Here, we present a new approach exploiting superradiance to engineer dynamical tunneling in a synthetic lattice geometry. Our experimental implementation is based on a spinor Bose-Einstein condensate (BEC), which is coupled to a single mode of an ultrahigh-finesse optical cavity [1]. Transverse laser fields induce cavity-assisted Raman transitions between discrete momentum modes of two spin levels, which we interpret as photon-assisted tunnelling in a momentum-space lattice. In particular, the tunnelling rate evolves dynamically with the emergent cavity field. By monitoring the cavity leakage, we gain real-time access to the lattice currents and benchmark their collective behaviour [2].

In a series of recent experiments, we engineer an atomic mode parametric amplifier induced by virtual cavity photons. The spinor BEC is initialized in the |F = 1, mF = 0⟩ Zeeman sublevel (pump mode), and correlated pairs of atoms in |mF = ±1⟩ (signal and idler modes) are created by four-photon processes, which involve scattering of virtual cavity photons in a far-detuned regime. The pair production is highly non-linear, as evidenced by its scaling with atom number. Moreover, the spin pairs are ejected out of the BEC with opposite relative momenta, in resemblance parametric four-wave mixing. While similar to collisional spin-mixing dynamics [3], the timescales of this process (~10 μs) are significantly faster, providing prospects rapid entanglement production in cold atom experiments.

References
[1] F. Ferri, R. Rosa-Medina, F. Finger, N. Dogra, M. Soriente, O. Zilberberg, T. Donner, T. Esslinger,
(2021). Emerging dissipative phases in a superradiant quantum gas with tunable decay. Physical Review X, 11(4), 041046.

[2] R. Rosa-Medina, F. Ferri, F. Finger, N. Dogra, K. Kroeger, R. Lin, R. Chitra, T. Donner,
T. Esslinger, (2022). Observing dynamical currents in a non-Hermitian momentum lattice. Physical Review Letters, 128(14), 143602.

[3] L. Pezze, A. Smerzi, M.K. Oberthaler, R. Schmied, P.Treutlein, (2018). Quantum metrology with nonclassical states of atomic ensembles. Reviews of Modern Physics, 90(3), 035005.

17:00 Enhancing production of slow beams of laser-coolable molecules

Radical polyatomic molecules can be produced from gas-phase atomic metal precursors in the presence of a reagent gas. Previous work with YbOH [1] and CaOH [2] has shown that molecular production in a cryogenic buffer-gas cell can be enhanced more than ten-fold by populating metastable triplet electronic states of metal atom precursors. These demonstrations, while highly effective, required excitation of weak intercombination (i.e., spin-flip) transitions. Here we report work exploring alternative pathways to populate these metastable states via two-step excitation on strong transitions followed by spontaneous decay to the target states. Candidate pathways have been identified for calcium- and strontium-containing molecules. We present our results measuring enhancement factors for production of several molecules used in ongoing molecular physics experiments.

[1] Jadbabaie et al., New J. Phys. 22, 022002 (2020); [2] Zhang et al., J. Chem. Phys. 155, 091101 (2021)

17:00 Evaluation of the blackbody radiation shift uncertainty of the NRC strontium ion clock

At the National Research Council Canada (NRC), an optical frequency standard based on a single trapped strontium ion has been developed. The optical clock uses the 5s $^2S_{1/2}$ – 4d $^2D_{5/2}$ electric quadrupole transition of the $^{88}\mathrm{Sr}^+$ ion at 445 THz as its reference transition. This clock transition of the $^{88}\mathrm{Sr}^+$ ion has been recommended as one of the secondary representations of the SI second. Currently, the overall systematic uncertainty of NRC’s $^{88}\mathrm{Sr}^+$ ion clock is $1.2\times10^{-17}$ in fractional frequency units, which is mainly limited by the blackbody radiation (BBR) shift uncertainty of $1.1\times10^{-17}$.

The BBR shift is caused by the interaction of the energy levels of the clock transition with the electric field of the thermal radiation at the ion position. The BBR shift uncertainty of our $^{88}\mathrm{Sr}^+$ ion clock is mainly limited by the evaluation of the electric field caused by the thermal radiation. The other two parameters needed to determine the BBR shift, namely the polarizability and the dynamic correction of the clock transition, can either be measured or calculated accurately and their contributions to the uncertainty of the BBR shift is below $10^{-18}$.

In order to evaluate the thermal electric field experienced by the $^{88}\mathrm{Sr}^+$ ion in the optical frequency standard, we built a copy of ion trap and installed it in an offline vacuum chamber dedicated to thermal imaging measurements. A calibrated IR camera has been used to measure the temperature change of the test trap components when a drive rf voltage is applied to electrodes. To increase the accuracy of the temperature measurements using the IR camera, key trap components were painted with matte black paint to increase emissivities. The temperature data of the test trap components will be compared to a finite element simulation from which the effective thermal electric field experienced by the $^{88}\mathrm{Sr}^+$ ion can be extracted for the evaluation of the BBR shift and its uncertainty.

It is expected that the overall uncertainty of the $^{88}\mathrm{Sr}^+$ ion optical clock will be reduced to the $\sim5\times10^{-18}$ level with the results of the current study.

17:00 Experiment and theory for a helium tune-out frequency: an independent test of quantum electrodynamics

Quantum electrodynamics (QED) is one of the most stringently tested theories underpinning modern physics. Nevdertheless, recent precision atomic spectroscopy measurements have uncovered several small discrepancies between experiment and theory. One particularly powerful experimental observable that tests QED independently of traditional energy level measurements is the tune-out frequency, where the dynamic polarizability vanishes and the atom does not interact with applied laser light. In our work, we measure the tune-out frequency for the $2\;^3S_1$ state of helium between transitions to the $2\;^3P_J$ and $3\;^3P_J$ manifolds and compare it with new theoretical QED calculations [1]. The experimentally determined value of 725,736,700(260) MHz differs from theory [725,736,252(9) MHz] by 1.7 times the measurement uncertainty and resolves both the QED contributions and retardation corrections. The underlying theory is formulated more generally as a zero in the forward Rayleigh scattering cross section, rather than a zero in the dynamic polarizability. Relativistic, QED, and retardation corrections are included in a nonrelativistic QED (nr-QED) approach

[1] B. M. Henson et al., Science 376, 199 (2022).

17:00 Experimental Upgrades For Improving Statistical And Systematic Uncertainties In ACME III

The measurement of the electron electric dipole moment (eEDM), $d_e$, is a powerful probe of physics beyond the Standard Model. The current most stringent limit of $|d_e|<1.1\times10^{-29}\ \textrm{e}\cdot\textrm{cm}$ was reported by the ACME II experiment (Nature, 562(2018), 355). ACME III aims to improve this experimental limit by an order of magnitude. Progress has been made in improving the statistical sensitivity. An electrostatic lens that can increase the flux of a ThO molecular beam has been built and tested. We are also upgrading our fluorescence detectors to silicon photomultipliers for higher quantum efficiency. An upgraded cryogenic buffer gas beam (CBGB) source featuring shorter cool-down time and in-situ target changing function is built for increasing the duty cycle of the experiment. Guided by our recent H $^3\Delta_1$ lifetime measurement, a longer interaction region is constructed. We also made progress toward reducing systematic errors and their uncertainty. One significant source of systematic error comes from birefringence gradients in the laser optics. We are implementing a modified measurement scheme to reduce this systematic error and taking several new measures to reduce birefringence gradients. Last, we are building and testing an upgraded magnetic shielding and field control system.

Related publications: Electrostatic lens, H state lifetime, SIPM upgrades.

*This work was supported by the National Science Foundation, the Gordon and Betty Moore Foundation, the Alfred P. Sloan Foundation, JSPS Kakenhi, and Okayama University RECTOR program.

17:00 Exploring the Lithium Few-Body Puzzle with the DITRIS Interferometer and with Minimal Multi-Channel Models

In the vicinity of a Feshbach resonance only a hand full of length scales, such as the scattering length and the effective range, determine the observed physics. Few-body observables, such as recombination loss maxima and minima, are related to the underlying length scales via universal theories. In particular, the Efimov-van-der-Waals universality relates the position of the first three-body recombination resonance on the negative scattering length side to the van-der-Waals length according to the Feshbach resonance strength. While numerous experiments in several species seem to verify this universality, Lithium was found to defy it.
Here we use coherent few-body spectroscopy (the DITRIS interferometer) to explore the positive scattering length side in Lithium. By creating a superposition of two different loosely bound states, Feshbach dimers and Efimov trimers, we measure the Efimov binding energy relative to that of the dimer. It is applied to the theoretically controversial and experimentally demanding regime, where the first excited trimer supposedly merges with the dimer-atom continuum. Contrary to the universal expectation we discover that it crosses into the continuum and remains a long-lived bound state.
In an attempt to explain this observation, we build minimal models including the dominant multi-channel contributions to the long-range physics. In two separate models we add either an additional closed or open channel – both of which are present in Lithium. The failure of these models to replicate the experiment indicates that, in addition to the multi-channel character of the interactions, the short-range details of the interaction potential are necessary. This is in stark contrast to the assumption of universality.

17:00 Fast Preparation and Detection of a Rydberg Qubit Using Atomic Ensembles

Arrays of neutral atoms have recently emerged as a competitive platform for quantum simulation and computation with many properties favorable for scaling. Rydberg states of atoms are often used because the strong Rydberg-Rydberg interactions can facilitate two-qubit gate operations and simulate many-body systems. However, for most schemes, readout of a Rydberg qubit is a destructive process that precludes its reuse and the application of many error-correcting codes. To address this challenge, we demonstrate a nondestructive implementation of preparation, manipulation, and readout of a single Rydberg qubit embedded in an atomic ensemble with high fidelity. By harnessing the collective optical response of the atomic ensemble, we detect the state of a qubit ~1000x faster than single-atom fluorescence imaging. This method determines the state of the Rydberg qubit without affecting the other atoms in the ensemble to first order, which can then be reused for further operations. With this developed technique, we are making progress towards realizing a quantum computer based on arrays of atomic ensembles, which can significantly improve the computation speed.

17:00 From a polaron into a cluster: the fate of an impurity in a Bose-Einstein condensate

Ultracold atomic gases can be used to simulate phenomena from condensed matter physics, such as the formation of polaron quasiparticles. However, at strong coupling a Bose polaron formed by an impurity atom in a Bose Einstein condensate (BEC) displays fascinating behavior quite distinct from the common condensed matter scenario. This is due to the possibility of bound state formation and the Efimov effect, which leads to attractive impurity-mediated interactions between the bosons from the BEC. In particular, the intricate competition between these impurity-mediated interactions and the intrinsic interboson repulsion plays an important role. In our work we fully incorporate both of these processes and compare different variational methods to form a complete theoretical picture of the strong coupling Bose polaron. We find two parameter regimes with qualitatively different behavior. For light impurities and weak repulsion, the impurity-mediated interactions dominate and we find a polaronic instability due to the formation of large Efimov clusters. For strong repulsion or heavier impurities, we find that the formation of large clusters and the polaronic instability are prevented, and that there is a smooth crossover into a small cluster or molecule instead.

17:00 From superradiance to subradiance : exploring the many-body Dicke Ladder

We are interested in the problem of light scattering by a dense ensemble of two-level atoms in a regime close to the Dicke regime, in which many atoms are trapped in a volume whose dimensions are smaller than the wavelength of the atomic transition. When the medium is dense and the frequency of the light is close to that of an atomic transition, the light-induced dipoles interact with each other. These resonant interactions between the dipoles modify the collective response of the ensemble. Here we report a time-resolved study of collective emission in dense ensembles of two-level atoms.

We compare, on the same sample, the build-up of superradiance and subradiance from the ensemble when driven by a strong laser. This allows us to measure the dynamics of the population of superradiant and subradiant states as a function of time. We demonstrate the buildup in time of subradiant states through the superradiant dynamics. This illustrates the dynamics of the many-body density matrix of superradiant ensembles of two-level atoms when departing from the ideal conditions of Dicke superradiance in which symmetry forbids the population of subradiant states.

17:00 Generation of photons from vacuum in cavity via time-modulation of a qubit invisible to the field

Dynamical Casimir effect (DCE) designates a plethora of phenomena characterized by generation of photons (or quanta of some other field) from vacuum due to time-dependent variations of the geometry (dimensions) or material properties (e.g., the dielectric constant or conductivity) of some macroscopic system. The circuit QED architecture is a handy platform for the implementation of DCE and its analogues, since both the cavity's and artificial atoms' properties can be rapidly modulated by external magnetic field. In particular, the generation of photons and light-matter entangled states from the initial vacuum state can take place for a resonant time-modulation of the atomic transition frequency or the atom-field coupling strength, when the atom is directly coupled to the field via the dipole interaction (as described by the Quantum Rabi Model). In this case, one can think of the atom as a microscopic constituent of the intracavity medium. Here we propose a scheme for the generation of photons from vacuum due to the time-modulation of some quantum system that is "invisible" to the field, namely, some artificial 2-level atom (nonstationary qubit) that is indirectly coupled to the field via some ancilla quantum subsystem. We consider the simplest case when the ancilla is a stationary qubit, coupled via the dipole interaction both to the cavity field and the nonstationary qubit, but our results can be easily generalized to more complex atoms. We find that a small number of photons can be generated from the system ground state under resonant modulations even when the nonstationary qubit is far detuned from both the ancilla and the cavity. Moreover, for specific relations between the natural frequencies of the three subsystems the photon generation rate can be strongly enhanced due to the anti-crossings in the energy levels of the bare Hamiltonian, when the system is driven to a triparite entangled state. We attest our approximate analytic results by numeric simulations and show that the photon generation from vacuum persists even in the presence of common dissipation mechanisms. Thus, our scheme could find applications in the engineering of effective interactions and entangled states in hybrid cavity QED systems, when the nonstationary qubit is designed to undergo fast large-amplitude modulations, while the cavity field is coupled to another stationary atom.

Speaker: Alexandre Dodonov (University of Brasilia)

Generation of photons from vacuum in cavity via time-modulation of a qubit invisible to the field

17:00 High-Precision Mass Measurements of Light Atomic Nuclei: The Helium-4 Atomic Mass

Atomic masses with high precision can be determined by Penning-trap mass spectrometry. The LIONTRAP experiment is one such high-precision mass spectrometer that can achieve relative mass uncertainties of the order of 10$^{−12}$ and is dedicated to light ions. Measurements on light ions are challenging due to the relatively large ratio of kinetic energies compared to the low rest mass.

The results at LIONTRAP include the atomic mass measurements of the proton [1], the deuteron and the HD$^+$ molecular ion [2]. The deuteron mass was measured to a relative precision of 8.5 ppt [2]. Our results show an excellent agreement with values that were extracted from laser spectroscopy of HD$^+$ [3]. This comparison is currently limited by the precision of the electron’s mass in atomic mass units (amu), derived from a measurement of the bound electron ${\it g}$-factor in $^{12}$C$^{5+}$ [4]. $^4$He is a prime candidate for a future improvement, as it is far less sensitive to higher-order terms of quantum electrodynamics (QED) and to the charge radius of the nucleus. Currently, we have measured the atomic mass of $^4$He to support such a determination of the electron mass in amu.

Furthermore, an ultra-precise measurement of the mass difference of $^3$He and $^3$T will provide an important crosscheck of the determination of the electron anti-neutrino mass with the KATRIN experiment [5]. Moreover, $^3$He to $^{12}$C mass ratio could further clarify the so-called ‘puzzle of the light masses’, which is an inconsistency in the values of light masses from different world-leading experiments [2]. In this contribution, the present status of the experiment will be discussed.

[1] F. Heiße $\textit{et al}$., Phys. Rev. A $\textbf{100}$, (2019).
[2] S. Rau $\textit{et al}$., Nature $\textbf{585}$, pp. 43-47 (2020).
[3] I. V. Kortunov $\textit{et al}$., Nature Physics, $\textbf{17}$, pp. 569-573 (2021).
[4] S. Sturm $\textit{et al}$., Nature $\textbf{506}$, pp. 467-470 (2014).
[5] KATRIN Collaboration, Nature Physics, $\textbf{18}$, pp. 160-166 (2022).

17:00 Integrability, ultracold matter and quantum sensing

The development of novel quantum technologies ultimately depends on the ability to generate non-classical states. In this regard, the so-called "NOON states" - "all or nothing" superpositions - have been shown to enable interferometry at the "Heisenberg sensitivity" (with a scaling that is limited by nature itself). Much effort has been made to generate such states on several platforms, with the main limitation being the number of occupied modes in each subspace. Here, we propose the use of integrability to circumvent this issue. Considering a system of interacting dipolar atoms hopping along the edges of a square plaquette, we introduce two different protocols for the generation of NOON states with scalable mode occupation. An experimental realization based on optical superlattices is proposed, which would allow for the realization of the integrable regime in the system.

17:00 Interferometry on the Clock Transition in Sr-87 with Entangled Atoms in Momentum State Superpositions

I will present our activity on the realisation of atom interferometry with an optical clock transition beyond the standard quantum limit (SQL) with strontium atoms. An interferometer can be injected with entangled atoms to improve its phase resolution $\Delta \phi$, where the entanglement is created between momentum state superpositions by performing cavity-enhanced quantum non-demolition (QND) measurements [1]. Our method will improves the scaling in phase resolution $\Delta \phi$ with atom number $N$ surpassing the SQL of $\Delta \phi \sim N^{-1/2}$ for uncorrelated atoms. An interferometer using a similar method for entanglement creation has recently been demonstrated for a small atom number $N$ and a short interrogation time $T$ using rubidium atoms [2].

Atom interferometry can be used to study fundamental physics, like testing the equivalence principle or determining the gravitational constant $G$. It can furthermore be used in Earth observation sciences and in future space applications. To reach small phase resolutions $\Delta \phi$ interferometers need large-momentum transfer, a large atom number $N$ and a long interrogation time $T$. However, many applications are limited by the size, weight and power consumption of the instrument, this is especially true for space applications. An interferometer implementing QND measurements can therefore be reduced in size, weight and power consumption compared to interferometers using uncorrelated atoms. Furthermore, when using squeezing a given precision is reached after a smaller averaging time, which improves the sensor bandwidth.

We plan to create an atom interferometer on the clock transition ${^1S_0} \leftrightarrow {^3P_0}$ in $\text{strontium-87}$ [3] and inject it with entangled atoms using QND measurements. We realised a narrow-linewidth clock laser system at 698 nm to drive the clock transition. We are working on a homodyne detection system to perform the QND measurements. A momentum state superposition will be created between ${\left\vert {^1S_0}, p = 0 \right\rangle}$ and ${\left\vert {^3P_0}, p = \hbar k \right\rangle}$ using single-photon transitions at 698 nm, with $\hbar k$ the momentum of a single photon. The QND measurements will be performed by probing the wave packets detuned from the ${^1S_0} \leftrightarrow {^3P_1}$ transition at 689 nm when they cross the focus of the high-finesse experimental cavity. Squeezing will be induced by measuring the populations in the prepared superposition. At the end of the interferometer sequence the population difference will be read out with increased sensitivity. This method can be used with other atomic species where a narrow transition is available or can be created.

[1] L. Salvi et al., Phys. Rev. Lett. $\textbf{120}$, 033601 (2018).
[2] G.P. Greve et al., arXiv $\textbf{2110}$, 14027v1 (2021).
[3] L. Hu et al., Class. Quantum Grav. $\textbf{37}$, 014001 (2020).

17:00 Laser cooling AlCl molecules in the deep-ultraviolet

Laser-cooled molecules promise access to a diverse range of research directions from quantum simulation to controlled ultracold chemistry. Today, inefficient slowing of cold molecular beams remains a key barrier preventing molecular magneto-optical traps (MOTs) from trapping large, dense samples of ultracold molecules with properties similar to their atomic counterparts. Our experiment aims to remove this barrier by using bright continuous beams of cold molecules [1] and a molecular species susceptible to large optical forces by photon scattering. Our molecule of choice, aluminum monochloride (AlCl) has favorable properties for laser cooling and efficient trap loading, including a lack of spin-rotation structure and strong optical transitions in the deep-ultraviolet. Here we will present our latest work spectroscopically characterizing and manipulating a beam of AlCl with multiple high-power ultraviolet lasers [2].

[1] J. C. Shaw and D. J. McCarron Phys. Rev. A 102, 041302(R) (2020).
[2] J. C. Shaw, S. Hannig and D. J. McCarron Opt. Express 29, 37140 (2021).

*This work is supported by the NSF (CAREER Award No. 1848435) and the University of Connecticut, including a Research Excellence Award from the Office of the Vice President for Research.

17:00 Laser cooling Cd atoms and AlF molecules in the deep UV

We present our recent results on the fast loading of a dense magneto-optical trap (MOT) of Cd atoms from a pulsed cryogenic helium buffer gas beam. We can load more than $10^7$ atoms of each Cd isotope in less than 10 ms from a single atomic pulse and reach densities well above $10^{11}$ cm$^{-3}$ by using the strong transition in the deep ultraviolet near 229 nm. The Cd MOT serves as a starting point for precise isotope shift measurements to search for new physics beyond the Standard Model of particle physics. In addition, Cd is an excellent species to test our MOT apparatus to cool the diatomic, polar and deeply bound molecule AlF using the strong A$^1\Pi\leftrightarrow$X$^1\Sigma^+$ transition near 227.5 nm. We demonstrate the efficient production of AlF, and the implementation of a simple and fast optical cycling scheme. As a first application, we reduce the transverse temperature of a molecular beam of AlF by using a blue-detuned optical molasses. Finally, we discuss the implementation of a Zeeman slower and a MOT for AlF.

17:00 Low-Phase-Noise Diode Laser Systems for the STIRAP transfer of Ultracold $^6$Li$^{40}$K Molecules

In our group, we are interested in $^6$Li$^{40}$K molecules at their rovibrational ground-state, which posses a large $3.6~\text{Debye}$ absolute dipole moment. This makes them suitable for the quantum many-body simulation of anisotropic and long range interactions. In order to transfer the molecules from a weakly bounded Feshbach-state to their ground-state, the method to be used is stimulated raman adiabatic passage (STIRAP). Excessive residual laser phase noise will drive unwanted transitions and therefore decrease the STIRAP efficiency. To deal with this issue, we extended the length (from 2 cm to 20 cm) of our external cavity diode lasers to narrow the free-running linewidth. The phase noise measurement method consisted in recording the spectral noise density of the beat note produced between the laser and a high-finesse cavity filtered version of itself. The integrated phase noise was reduced from 200 mrad to 40 mrad.

Theoretical calculations of the STIRAP efficiency also show the critical dependence on the pulse duration. The stochastic nature of the phase noise means that to reduce its effect, the pulse duration should be reduced. But on the other hand one should consider that the pulse should not be too short such that the adiabaticity criterion is violated. Additionally, we included tapered amplifiers to increase the Rabi frequency while preserving the low phase noise of the long external cavity diode lasers.

17:00 Many-body Quantum Necklace States in Waveguide QED

The field of waveguide QED, where atoms (real or artificial) are coupled to one-dimensional waveguides, has attracted immense theoretical and experimental interest recently. However, despite the huge body of research, our understanding of the many-body regime consisting of many atoms and photons remains limited. This stems partly from the usual challenge of many-body systems – the exponentially large Hilbert space size – and also from the intrinsically open and non-equilibrium nature of waveguide QED systems. Recently, it has been theorized that the dynamics in disordered waveguide QED systems can exhibit a many-body localized phase, where the underlying Hamiltonian becomes diagonalizable in terms of local integrals of motion and the dynamics can be solved in a non-perturbative fashion. Moreover, a dynamical phase transition is predicted between delocalized, many-body localized, and Anderson localized phases as a function of the density of excitations in the system. We hypothesize that the microscopic mechanism responsible for said phase transition is the formation of extended “necklace” states that facilitate transport across the system. These states are formed by the hybridization of localized modes of different resonance frequencies that span the system length, and can facilitate tunneling of photons in combination with interactions in the form of quantum nonlinear frequency mixing. We discuss our ongoing efforts to show that these quantum necklace states dominate quantum transport of photons in disordered waveguide QED, and how they manifest themselves in accessible observables like the transmission spectra, two-photon correlations, and their fluctuations.

17:00 Measurement-Based Quantum Machine Learning

Quantum machine learning (QML)---machine learning on quantum computers---is a rapidly developing, promising application of near-term quantum devices. Most present hardware implements the unitary circuit model of quantum computation. However, recently also measurement-based quantum computation (MBQC) has become technologically relevant, and progress is made towards MBQC with atomic systems. So far, measurement-based QML (MB-QML) has almost not been considered. We introduce a general framework for MB-QML on classical and quantum data. Specifically, we propose a universal building block to construct ansätze for unitaries, measurements, and channels, and discuss how to constrain these ansätze. Our algorithm successfully learns unitaries and classifies quantum states for small systems, proving robust to noise. This work lays the foundation for QML on MBQC devices.

17:00 Measurement-only phase transitions in 2D via non-commuting two qubit measurements

Motivated by the extensive studies of measurement-only entanglement phase transitions in 1D, we implement a simple model of random non-commuting two qubit XX and ZZ measurements in 2D. We tune the probability of measuring XX and ZZ on horizontal and vertical bonds and use long range spin correlations as the order parameter. We find that when the system has subsystem symmetries, we get a second order phase transition and a critical point with logarithmic violation of area law. Without the subsystem symmetries, the transition immediately turns into a crossover. We also find points where long range spin correlation along rows and columns show a discontinuous phase transition. We also draw connections of this model to the error correcting Bacon-shor code.

17:00 Mollow Triplet in optically trapped single atom

Resonance fluorescence spectrum of a two-level system consists of a single peak that evolves into a triplet structure, known as Mollow triplet , when it is driven by a radiation field above its saturation intensity. Particularly, photons originated from different peaks of the triplet show distinct photon correlations, which allows the fluorescence to be engineered as a useful light source for quantum information processing purposes. Surprisingly, the Mollow triplet was never studied for an optically trapped single atom given the advantages it has. We study experimentally the fluorescence spectrum of an optically trapped single $^{87}$Rb atom by exciting a closed two-level transition with an on-resonant laser at different powers. The second-order intensity correlation measurement demonstrates the photon anti-bunching characteristic from a single atom emission as well as the Rabi oscillation undergone by the atom. Next, we measure the cross correlation between photons coming from the two sidebands of the fluorescence spectrum when an off-resonant field is applied on the atom. The asymmetry in the timing correlation clearly indicates that there is a preferred time-ordering for the photon emission process in the two sidebands. The cascaded generation of time-correlated fluorescence photons with a tunable frequency difference will be useful for quantum optics experiments and quantum communication protocols.

17:00 Muonium 1S-2S spectroscopy with improved statistics

Our purpose is precision measurement of the 1S-2S energy interval in Muonium, which is an exotic hydrogen-like atom consists of a positive muon and an electron. This purely leptonic system enables a precise calculation of the energy interval with the Standard Model without any concerns of the uncertainty from the charge radius of the nucleus, unlike the hydrogen-atom. This advantage motivates us to measure the precise 1S-2S energy interval in Muonium with technology of laser spectroscopy and to determine the muon mass with the highest accuracy of 10 ppb. The improvement of muon mass accuracy has an impact on verification of the Standard Model, muon g-2/EDM experiment, for example.

The energy interval accuracy has been statistically limited since 1999[1]. However, more powerful muon beam is available now at J-PARC in Japan and we are developing new UV laser system.

We will report a recent result of Muonium 1S-2S energy interval measurement at J-PARC. The event rate in our experiment is 50 times higher than the previous experiment. This dramatic improvement gives promising prospect for higher accuracy of 1S-2S energy interval and the muon mass accuracy in the future.

[1]V. Meyer et al, Phys. Rev. Lett 84, 1136(2000)

17:00 New Applications and Current Limitations of Rydberg Sensors

Electric field sensors based on warm vapors of atoms excited to Rydberg states have distinguishing features that offer new application possibilities. A single sensor can operate over a wide spectrum of frequencies, from DC to THz, with a consistent instantaneous baseband bandwidth of approximately 10MHz. The sensor head containing the vapor is highly transparent and can also be small relative to the electric field wavelengths, enabling accurate measurements with sub-wavelength spatial resolution. Presently Rydberg sensors rely on the spectroscopic method of electromagnetically induced transparency (EIT) for preparing and probing the atoms, and though simple and effective, this places limits on the sensitivity and instantaneous bandwidth of the sensor. We numerically and experimentally investigate this limit for Doppler-broadened optically thick samples, and show the optimal EIT parameter regime. We further present recent results on new applications, such as a Rydberg-backend spectrum analyzer with field sensitivity of -145dBm/Hz and dynamic range >80 dB.

17:00 New Perspectives on Quantum Transition Times: The Tunneling Flight Time

Recent experimental and theoretical works have reignited long-standing debates over the time taken for certain quantum transitions, such as tunneling, to occur. This is important, as tunneling is a common quantum phenomenon in molecular systems where nonadiabatic couplings are significant, and certain simulation methods struggle to accommodate its effects. Here we propose a new type of quantum mechanical flight time, based on weak-averaging, and show the conditions under which it becomes equal to another measure known as the phase time. We compare these results to recent Larmor time experiments for tunneling, and show that the Larmor time and dwell time coincide under the same circumstances as the new flight time and the phase time. Finally, we discuss ongoing work to evaluate flight times in two-level systems with strong nonadiabatic couplings emulating certain electronic transitions, and show the effects nonadiabatic couplings have on tunneling times.

Speaker: Tom Rivlin (Weizmann Institute of Science)

17:00 Next-Generation Strontium Ion Optical Atomic Clocks

The performance of optical atomic clocks has improved tremendously over the last two decades. The fractional frequency uncertainties of the best optical clocks reach the $10^{-18}$ level and currently outperform cesium fountain clocks, the current primary frequency standards defining the SI second, by two orders of magnitude. Redefinition of the SI second based on optical clocks is expected to take place in the next decade. The criteria require that optical clocks are evaluated with fractional frequency uncertainties of $3\times 10^{-18}$ or better, and compared with other devices in remote laboratories with uncertainties comparable to their evaluated uncertainties. In recent years, the frequency and time group at the National Research Council Canada (NRC) has been developing a high-accuracy transportable optical atomic clock for direct comparisons with clocks in other National Metrology Institutes.

The optical clock at NRC is based on the 445-THz $5s\,^{2}S_{1/2}\,$-$\,4d\,^{2}D_{5/2}$ electric quadrupole transition in $^{88}$Sr$^{+}$. The frequency reference is a single laser-cooled ion, suspended between two endcap electrodes with a radio-frequency (RF) electric field. An optical clock based on $^{88}$Sr$^{+}$ is well suited for the transportable system due to its simple energy-level structure, where only four lasers with easily accessible wavelengths are required for its operation. Furthermore, the systematic effects that perturb the clock transition are well understood, and can be controlled at or below the $10^{-18}$ level. Our transportable system is equipped with a newly-designed ion trap with improved thermal properties that is expected to reduce the blackbody radiation shift (BBRS) uncertainty by an order of magnitude compared to our existing stationary clock. It also has a compact vacuum chamber with 10 times lower background gas pressure, which is expected to reduce the collisional frequency shift (CFS) by the same factor.

With these upgrades, all the systematic effects in the transportable system are expected to be below the $10^{-18}$ level. For further improved performance, we have recently started to build a cryogenic $^{88}$Sr$^{+}$ optical clock, where both the BBRS and CFS will be suppressed below the $10^{-19}$ level. Future comparisons between cryogenic and transportable clocks will validate the accuracy of our ensemble of $^{88}$Sr$^{+}$ clocks.

We will present a brief overview of our $^{88}$Sr$^{+}$ clock system, and the current status and future prospects of both the transportable and cryogenic systems.

17:00 Novel Quantum Control Methods in a Rubidium-87 Bose-Einstein Condensate

Ultracold neutral atoms are an excellent test-bed for novel quantum control techniques due to their stability, and efficient coupling to fields in the radio, microwave, and optical regimes. Various control protocols which could be used in quantum information processing (QIP) may first be investigated in ultracold atoms to prove their efficacy before being generalized to other more established systems. In this spirit we present two different novel control protocols. First we demonstrate holonomic single-qubit gates, which are conventionally performed via the adiabatic evolution of a degenerate manifold of states through a path in parameter space; this yields a non-Abelian geometric phase which couples the states in a way that depends only on the path taken. In this study, we eliminate the explicit need for degeneracy through Floquet engineering, where the atomic spin Hamiltonian is periodically modulated in time. We characterize the non-Abelian character of the geometric phase through a gauge-invariant parameter, the Wilson loop. Next, we demonstrate a decomposition of SU(3) including a resonant dual-tone operator which synthesizes coupling between two disconnected qutrit levels. For many conventional systems where the third coupling is not possible this technique provides a potential workaround. A decomposition of SU(3) using this operator is tested against conventional methods by performing a Walsh-Hadamard gate and performing maximum likelihood tomography on the resulting states. In both protocols we demonstrate novel methods for precision quantum control essential in advancing QIP techniques which can be readily adapted to trapped ions, superconducting qubits, and other quantum computing platforms.

17:00 On Demand Formation of Polar Core Vortices in Ferromagnetic Spinor Bose Einstein Condensates

Spinor BECs are Bose-Einstein condensates (BECs) where all the spin states {$m_F=+1,0,-1$} of the atom are accessible [1]. These novel ultracold atomic systems can exhibit both ferromagnetic and antiferromagnetic order and thus offer enhanced opportunities for exploring phenomena beyond those accessible in scalar BECs, such as new classes of topological defects [2]. The polar core vortex (PCV) is one such topological defect occurring in the easy-plane phase of ferromagnetic spinor BECs. A PCV exhibits 2π spin circulation, but with zero mass circulation where the vortex core is populated by unmagnetized atoms in the $m_F=0$ state. The first experimental observation of a PCV was achieved by Sadler et al [2] in 2006, where the vortex spontaneously formed during a magnetic field quench. Due to the non-deterministic nature of creating PCVs, further experimental study of their properties and dynamics has been limited. Controlled creation of PCVs can enable such studies, including few-body PCV dynamics, PCV turbulence, and the equilibrium dynamics of PCV systems. In this work, we describe our efforts to realize on-demand PCV creation in quasi-2D $Rb^87$ spinor BECs with uniform density enabled by digital-micromirror devices (DMD) optical traps [3].

[1] D. M. Stamper-Kurn, M. R. Andrews, A. P. Chikkatur, S. Inouye, H.-J. Miesner, J. Stenger, W. Ketterle, Optical Confinement of a Bose-Einstein Condensate, Phys. Rev. Lett. 80 (1998) 2027–2030.
[2] L. E. Sadler, J. M. Higbie, S. R. Leslie, M. Vengalattore, D. M. Stamper-Kurn, Spontaneous symmetry breaking in a quenched ferromagnetic spinor Bose-Einstein condensate, Nature 443 (2006) 312.
[3] Gauthier, G.; Lenton, I.; Parry, N.M.; Baker, M.; Davis, M.J.; Rubinsztein-Dunlop, H.; Neely, T.W. Direct imaging of a digital-micromirror device for configurable microscopic optical potentials. Optica 2016, 3, 1136–1143. doi:10.1364/OPTICA.3.001136.

17:00 On the prospects of optical cycling in diatomic cations: Effects of transition metals, spin-orbit couplings, and multiple bonds

Molecules with optical cycling centers (OCCs) are highly desirable in the context
of fundamental studies as well as applications (e.g., quantum computing) because they can be effectively cooled to very low temperatures by repeated absorption and emission (hence, cycling). Charged species offer additional advantages for experimental control and manipulation. We present a systematic computational study of a series of diatomic radical-cations made of a d-block metal and a p-block ligand, that are isoelectronic (in their valence shell) to the successfully laser-cooled neutral molecules. Using high-level electronic structure methods, we characterize state and transition properties of low-lying electronic states and compute Franck-Condon factors. The computed branching ratios and radiative lifetimes reveal that the electronic transitions analogous to those successfully used in the laser cooling of neutral molecules are less than optimal in the cations. We propose alternative transitions suitable for optical cycling and highlight trends that could assist future designs of OCCs in charged or neutral molecules.

17:00 One- and two-axis squeezing via laser coupling in an atomic Fermi-Hubbard model

We study the Ramsey-type spectroscopy and the production of spin-squeezed states with ultra-cold atomic fermions described by the Fermi-Hubbard model in the Mott insulating regime. We show activation of two twisting mechanisms by a position-dependent laser coupling between internal degrees of freedom of atoms. A single laser coupling simulates the one-axis twisting model with the axis and direction of squeezing determined by the value of phase defining the atom-laser coupling. As such, adding a second laser beam with an adequately chosen phase paves the way to simulate the two-axis counter-twisting model, allowing reaching the Heisenberg-limited level of squeezing. The scheme can be implemented readily in state-of-the-art optical lattice clocks.

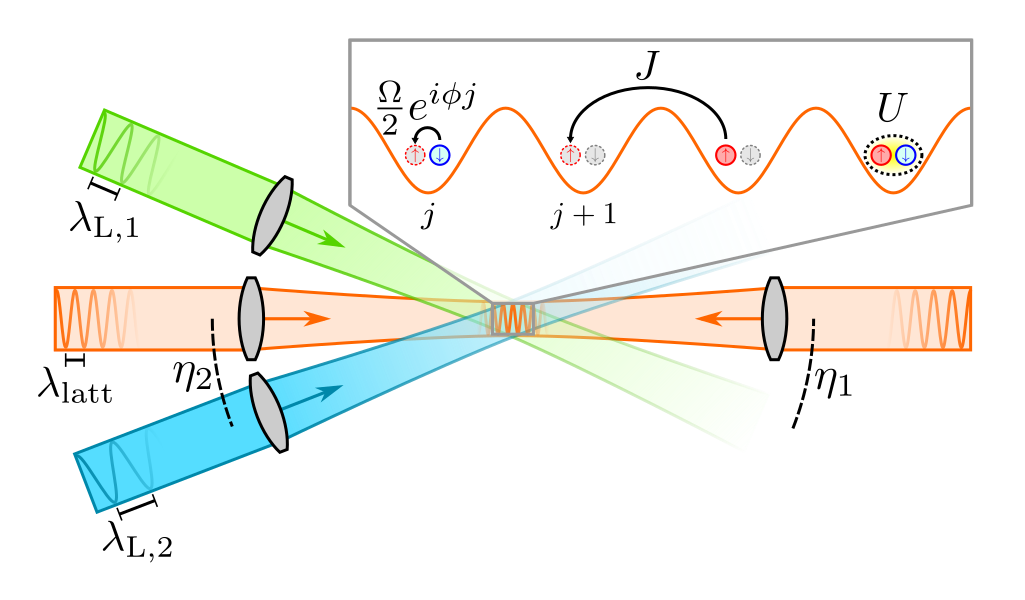Speaker: Tanausú Hernández Yanes (Institute of Physics PAS, Aleja Lotnikow 32/46, 02-668 Warszawa, Poland)

17:00 Orbital Feshbach Molecules

Spin-polarized samples, spin mixtures and Feshbach molecules of quantum degenerate fermionic atoms are prepared in selected excited Bloch bands of an optical chequerboard square lattice. For the spin-polarized case, extreme band lifetimes above 10 s are observed, reflecting the suppression of collisions by Pauli’s exclusion principle. For spin mixtures, lifetimes are reduced by an order of magnitude by two-body collisions between different spin components, but still remarkably large values of about one second are found [1].
Access to a broad Feshbach resonance allows for precise control of the interactions between atoms and molecules. Collision dynamics and binding energies of orbital Fermi gases in the unitary regime and are investigated for the first time. Remarkably long lifetimes of dimers in the second Bloch band on the onset of the unitarity regime are observed. By analyzing momentum spectra and band populations, we can directly observe the orbital character of the optical lattice.

[1] M. Hachmann et al. , Phys. Rev. Lett. 127 033201, July 2021

17:00 Parametric excitations in a quantum gas with Bogoliuvob-de Gennes method

Quantum gases of bosons and fermions behave as superfluids, and for parametric excitations, the sample exhibit Faraday Waves, which obey a Mathieu equation. Therefore, to generate them, we need to consider a periodic modulation in a parameter of the system, e.g., the trap frequencies or contact interaction. From the experimental point of view, these excitations are manifested in trapped gas when the density pattern appears. Theoretically, these phenomena have been studied in a variational approximation using mean-field equations. For the case of a Bose-Einstein Condensate, the system is described by the Gross-Pitaevskii equation, and for a Fermi Unitary Gas the Extended Thomas-Fermi model is used. However, we believe that the natural way to study these excitations is using Bogouliubov-de Gennes (BdG) method, where the density modulation generates the excitations (phonons). The usual treatment in this theory is to consider a homogeneous gas. In this context, we present the description of Faraday waves using BdG method. As preliminary results, we consider a homogeneous case with a modulation of the contact interaction.

17:00 Progress in experimental control of trapped ion motional states with applications for CVQC and quantum sensing*

Motional modes of trapped ions have been shown to be a useful tool for quantum sensing as well as a potential platform for performing continuous variable quantum computing (CVQC) [1,2]. Both applications require the ability to prepare well-defined motional states with high fidelity. These states can be generated without the use of laser fields which could reduce the experimental overhead in future systems. We report our progress towards generation of single and two-mode squeezed states as well as beam splitters [3] by means of parametric excitation. Additionally, we can apply displacements and phase shift operations. These operations comprise part of the tool box to create motional state interferometers such as the Mach-Zender or SU(1,1) interferometers and can be used to achieve Heisenberg limited phase sensitivities. In order to characterize these motional states, measurements require coupling the motion to the ions’ internal “spin” states followed by detection of spin-dependent fluorescence. Photon scattering, giving rise to fluorescence, causes the ion to recoil, which generally decoheres the ions’ motional modes. This decoherence prevents mid-algorithm measurements, which are necessary for processes that require classical feedback. To address this issue, we also describe progress towards the use of ‘protected’ [3] modes within chains consisting of an odd number of ions, where the center ion has zero displacement (3(N-1)/2 protected modes with N ions). The protection offered by these ions can be measured by analysis of the heating rates and coherence time of the protected mode during scattering events. *This research was supported by the U.S. Army Research Office through grant W911NF-19-1-0481 as well as support from NSF through the Q-SEnSE Quantum Leap Challenge Institute, Award # 2016244.
[1] S. Lloyd and S. L. Braunstein, Quantum Computation over Continuous Variables, Phys. Rev. Lett. 82, 1784 (1999)
[2] S. C. Burd, R. Srinivas, J. J. Bollinger1, A. C. Wilson1, D. J. Wineland,D. Leibfried, D. H. Slichter, D. T. C. Allcock, Quantum Amplification of Mechanical Oscillator Motion, Science 364, 6446 (2019)
[3] Pan-Yu Hou et al. Coherently coupled mechanical oscillators in the quantum regime, arXiv:2205.14841v1 (2022)

17:00 Progress Towards Precision Measurements in Trapped Polyatomic Molecules

The Standard Model as we know contains insufficient sources of charge parity (CP) violation to explain the observed baryon asymmetry of the universe (BAU). Heavy polar molecules are a sensitive, tabletop platform for precision searches of CP-violating electromagnetic moments originating from Beyond the Standard Model (BSM) physics. The polyatomic molecule YbOH is a promising platform to measure the electron electric dipole moment (eEDM); the electron localized around the Yb nucleus provides the ability to laser cool and trap the molecule, while the vibrational bending mode provides closely spaced parity doublets that allow for systematic error rejection and full alignment of the molecule in modest lab electric fields. Prerequisites for trapping YbOH molecules include developing an efficient molecular slowing scheme, identifying vibrational repump transitions, and spectroscopy on the excited states. Here we report on our progress developing a compact permanent magnet Zeeman-Sisyphus slower. We also report high-resolution frequency modulated (FM) absorption spectroscopy of the (300) stretching vibration in the electronic ground state of YbOH, and progress on excited state spectroscopy.
We acknowledge support from NIST, NSF, the Heising-Simons Foundation, the Gordon and Betty Moore Foundation, and the Alfred P. Sloan Foundation. Y.T. acknowledges support from the Masason Foundation. P.Y. acknowledges support from the Eddleman Fellowship.

17:00 Quantum computing with metastable states in trapped Barium ions

Trapped ion devices make some of the best candidates for quantum information processors as they provide naturally identical qubits with long coherence times. One approach to scaling these systems is using large registers of ions. This can be achieved through implementing qubits in multiple atomic species, where each qubit type is insensitive to the others' light fields, eliminating scattering errors. This allows for advanced qubit control and manipulation schemes. However, using multiple species adds significant experimental overhead [1].

An alternative to using multiple species is using long lived metastable states to encode, store, and manipulate quantum information. In our experiment, we use Barium ions, which have a metastable $5\text{D}_{5/2}$ manifold with a lifetime of $\sim30\,\text{s}$, long enough for quantum information processing. When combined with the stable $6\text{S}_{1/2}$ ground state manifold, we can gain all of the benefits of having two atomic species, while maintaining the technical simplicity of having just one [1,2]. Additionally, the Barium isotope we use, $^{137}\text{Ba}^{+}$, has nuclear spin 3/2, giving magnetically insensitive ‘clock’ qubits in both the $6\text{S}_{1/2}$ and $5\text{D}_{5/2}$ manifolds as well as ‘clock’ transitions between the manifolds. Both the ground state qubits and metastable state qubits can be driven using a 2-photon Raman process with 532nm light and very low scattering error.

We demonstrate individual manipulation of ‘clock’ qubits in these separate manifolds, a prerequisite for partial projective measurements and mid-circuit measurements. Such techniques can be used for error correction schemes using ancilla qubits. Additionally, we can perform in-sequence cooling of the ions to keep error rates low and constant.

References

[1] D. Allcock et al., Applied Physics Letters, vol. 119, p. 214 002, 2021.
[2] H.-X. Yang et al., arXiv preprint arXiv:2106.14906, 2021.

17:00 Quantum Control of Ultracold NaCs Ground State Molecules

We report on the creation of sodium-cesium (NaCs) molecules in their rovibrational ground state [1], assembled from ultracold clouds of Na and Cs atoms [2,3]. Via one- and two-photon spectroscopy we have identified a pathway that allows us to produce the first ultracold ensembles of NaCs ground state molecules via stimulated Raman adiabatic passage (STIRAP). In the ground state we explore the rotational structure. We demonstrate strong Rabi coupling on the microwave transition between the ground and first excited rotational state, allowing us to coherently control the rotational state on extremely fast time scales with pi-pulse times on the scale of 10 nanoseconds. The long-lived rotational states can be used as qubits or to shield the molecules from two-body loss. We show preliminary results on microwave shielding of the molecules, along with early work on direct evaporation of NaCs. Progress in this direction may allow cooling towards quantum degeneracy, potentially opening the door towards a strongly dipolar Bose-Einstein condensate of ground state molecules.
[1] I. Stevenson et al., arXiv:2206.00652 (2022)
[2] C. Warner et al., Phys. Rev. A 104, 033302 (2021)
[3] A. Z. Lam et al., Phys. Rev. Res. 4, L022019 (2022)

Speaker: Weijun Yuan (Columbia University)

17:00 Quantum Rabi dynamics of trapped atoms far in the deep strong coupling regime

The coupling of a two-level system with a field mode, whose fully quantized field version is known as the quantum Rabi model (QRM), is among the central topics of quantum physics and recent quantum information technologies. When the coupling strength reaches the field mode frequency, the full QRM Hamiltionian comes into play, where excitations can be created out of the vacuum.

We demonstrate a novel approach for the realization of a periodic variant of the quantum Rabi model using two coupled vibrational modes of cold atoms in optical potentials, which has allowed us to reach a Rabi coupling strength of 6.5 times the bosonic field mode frequency, i.e., far in the so called deep strong coupling regime. For the first time, the coupling term dominates over all other energy scales. Field mode creation and annihilation upon e.g., de-excitation of the two-level system here approach equal magnitudes, and we observe the atomic dynamics in this novel experimental regime, revealing a subcycle timescale raise in field mode excitations, in good agreement with theoretical predictions. We have also studied the collapse and revival of the initial state in the system. The current experimental status will be presented.

17:00 Quantum simulation with Rydberg states of lanthanide atoms

Lanthanide atoms provide a rich platform for a number of ultracold atom experiments due to their variety of available optical transitions, strong anisotropic interactions and the large spin space of their fermionic ground states [1]. Leveraging these properties alongside the large, programmable defect-free arrays of qubits that can be realised using optical tweezer arrays of Rydberg atoms promise to provide exciting systems for quantum simulation. Recent works using ytterbium have already demonstrated an enhanced tweezer loading scheme [2] and indicated that trapping Rydberg states is possible [3].

We present our progress in implementing a quantum simulator utilising Rydberg states of erbium trapped in an optical tweezer array. We have already identified approximately 550 states in the erbium Rydberg series including a possible state from the $ng$ series to which excitation is only possible due to the incompletely filled erbium $f$-shell [4]. Within our system the large 7/2 nuclear spin of the fermionic $^{167}\,$Er isotope will allow us to implement computational schemes involving up to 8-level qudit states. Additionally, we expect to find a large range of trappable erbium Rydberg states in our optical tweezers.

---

[1] M. A. Norcia and F. Ferlaino, Nature Physics 17, 1349-1357 (2021).
[2] A. Jenkins et al., Phys. Rev. X 12, 021037 (2022).
[3] J. T. Wilson et al., Phys. Rev. Lett. 128, 033201 (2022).
[4] A. Trautmann et al., Phys. Rev. X 3, 033165 (2021).

17:00 Rabi vector magnetometry implemented with hot alkali vapor

Optically-pumped magnetometers (OPMs) are widely used for their scalar sensitivity, accuracy, and compact sensor packages, but require additional mechanical references for vector magnetometry. These mechanical references, such as a coil system, often limit the vector accuracy due to machining tolerances and drifts. Current approaches to improve vector accuracy are calibrations that involve physical rotations of the magnetometer system at the expense of increasing the complexity of the physical apparatus. In this poster we demonstrate Rabi magnetometry as a novel approach to vector sensing with an OPM that utilizes a microwave polarization ellipse (MPE) as an accurate 3D reference.

The working principle of the Rabi magnetometer is to extract the orientation of a DC magnetic field relative to the MPE from Rabi rates driven coherently on a set of hyperfine transitions by a microwave field. Importantly, we calibrate systematics such as coil system and MPE drifts, pressure shifts, and Stark shifts from an accumulation of Rabi frequencies driven at various microwave detunings. Our measurements take place in a heated microfabricated vapor cell embedded within a microwave cavity; a platform with much greater sensitivity than a previous proof-of-concept experiment with cold atoms [1]. Depending on the direction of the DC magnetic field, we extract Rabi rates by either directly measuring Rabi oscillations or by fitting to sidebands in the Larmor free-induction-decay (FID) spectrum due to microwave dressing. Here we utilize the Faraday effect of a far-detuned probe beam to non-destructively sense atomic spin. With a full theoretical model, we understand the coherence of these Rabi oscillations to be dominated by spin-exchange collisions in a regime where current theoretical studies of hyperfine coherence that assume static atomic populations are not accurate.

References
[1] T. Thiele, Y. Lin, M. O. Brown, and C. A. Regal, Phys. Rev. Lett. 121 153202 (2018).

17:00 Rapid Quantum Squeezing by Jumping the Harmonic Oscillator Frequency

Quantum sensing and quantum information processing use quantum advantages such as squeezed states that encode a quantity of interest with higher precision and generate quantum correlations to outperform classical methods. In harmonic oscillators, the rate of generating squeezing is set by a quantum speed limit. Therefore, the degree to which a quantum advantage can be used in practice is limited by the time needed to create the state relative to the rate of unavoidable decoherence. Alternatively, a sudden change of harmonic oscillator’s frequency projects a ground state into a squeezed state which can circumvent the time constraint. Here, we create squeezed states of atomic motion by sudden changes of the harmonic oscillation frequency of atoms in an optical lattice. Building on this protocol, we demonstrate rapid quantum amplification of a displacement operator that could be used for detecting motion. Our results can speed up quantum gates and enable quantum sensing and quantum information processing in noisy environments.
Reference: Mingjie Xin, Wui Seng Leong, Zilong Chen, Yu Wang, and Shau-Yu Lan. Phys. Rev. Lett.127,183602(2021).

17:00 Scalable arrays of micro-fabricated Penning traps for quantum computation and simulation

Although radio-frequency (r.f.) traps have been widely used in trapped-ion quantum information and simulation, they face some inherent challenges in scaling up the number of qubits. Precise alignment of static and r.f. field nulls is necessary to achieve confinement of the ions without r.f. driven motion. As the r.f. null is inherently 1-dimensional, attempts at scaling into 2-d are beset by micromotion.

Instead we propose to use a two-dimensional array of Penning traps, implemented by micro-fabricated electrodes. Applying suitable electrical potentials to the surface electrodes generates an array of quadrupole fields above the chip, with a single ion trapped at each. This allows for individual control of secular frequencies and trapping heights with coupling provided by the Coulomb interaction. Micromotion and bulk crystal rotation are absent in this approach.

We have constructed an experimental apparatus containing the first micro-fabricated planar Penning trap in a 3 T field. The trap can produce a potential with two trap sites separated radially. To achieve ultra-high vacuum and low ion heating rates, the trap is held at cryogenic temperatures of around 6 K, with optics to allow for imaging and laser manipulation of ions as part of the cryogenic structure as well.

We report on our current efforts to initially trap ${^{9}{\rm Be}^{+}}$ ions in this setup. Potential challenges that may prevent successful trapping are identified. We attempt cooling of the radial motion by the axialisation technique, coupling the cyclotron and magnetron motions. The required strength of the weak coupling r.f. field is predicted as well as the precision of positioning of the r.f. null. Stray electric potentials may lead to unstable trapping conditions as well as perturb the axialisation frequency, requiring appropriate compensation. Neutral ${{\rm Be}}$ atoms are produced by pulsed-laser ablation, a process we have studied in depth.

17:00 Simulating Gauge Theories in $1+1$d with Bosonic Quantum Circuits

Quantum simulations of lattice gauge theories in qubits require a truncation of the infinite dimensional Hilbert space. This alters the behavior of the model. However, recent progress in the control of bosonic qubits, which naturally host a large dimensional Hilbert space, points the way to efficient simulation of lattice gauge theories in $1+1$d that generalizes well to higher dimensions. We consider novel and realistic implementations of these models in circuit QED, in two different experimental regimes. We analyze the phase diagrams with matrix product state simulations and implement a variational quantum eigensolver in Bosonic Qiskit - our extension of Qiskit to bosonic circuits - to obtain the ground states. Furthermore, we compare the complexity of simulating lattice gauge theories with qubit and circuit QED architectures, finding that the latter provides orders of magnitude higher efficiency. Our results may be generalized to higher dimensions and non-abelian field theories.

17:00 Simultaneous trapping and cooling of sodium and potassium atoms towards quantum degeneracy

We present the design, implementation and characterization of a new dual-species cold atomic mixture of $^{39}$K and $^{23}$Na with a large number of atoms. The dual species Magneto Optical Trap (MOT) has more than 10$^{10}$ $^{39}$K atoms and 5$\times$10$^9$ $^{23}$Na atoms, which are simultaneously loaded using two independent 2D$^+$MOT with high cold atomic beam flux. The dual cold atomic clouds were further cooled to tens of $\mu$K via sub-Doppler cooling and Gray molasses technique. The $^{23}$Na and $^{39}$K atoms are thereafter transferred into a quadrupole magnetic trap and transported towards the “Science cell” for further experiments. This versatile experimental system provides a favourable starting point for the realization of the quantum degenerate Bose-Bose mixture for quantum simulation with ultracold quantum gases in optical potentials.

Speaker: Mr Sagar Sutradhar (Ph.D. Student)

17:00 Size-energy universality in van der Waals self-bound systems

A universal relationship between scaled size and scaled energy was explored in few-body systems$^{1,2,3}$. Ground-state self-binding energies were obtained by the diffusion Monte Carlo method. Obtained energies support generalized Tjon lines. Structural properties were extracted by pure estimators$^4$, which proved successful in evaluating theoretical predictions of distribution functions$^5$ in comparison with the experimental Coulomb explosion imaging results$^{6,7}$.

Strengthening the inter-particle interaction, the exploration was extended from halo systems, which are extremely weakly bound and prefer to be in classically forbidden regions, to classical systems.

Universal size-energy law has been found for a homogeneous system of particles when pair-potentials decay predominantly with $r^{-6}$. The law is also valid for mixed systems with homogeneous-like structure.

References
1. P. Stipanović, L. Vranjš Markić, I. Bešlić and J. Boronat, Phys. Rev. Lett. 113, 253401 (2014).
2. P. Stipanović, L. Vranješ Markić, A. Gudyma and J. Boronat, Scientific Reports 9, 6289 (2019).
3. P. Stipanović, L. Vranješ Markić and J. Boronat, Scientific Reports (2022). DOI: 10.1038/s41598-022-13630-2
4. J. Casulleras and J. Boronat, Phys. Rev. B 52, 3654 (1995).
5. P. Stipanović, L. Vranješ Markić and J. Boronat, J. Phys. B: At. Mol. Opt. Phys. 49, 185101 (2016).
6. J. Voigtsberger et al., Nature Communications 5, 5765 (2014).
7. M. Kunitski et al., Science 348, 551 (2015).

17:00 Spin-charge separation in a 1D Fermi gas with tunable interactions

Ultracold atoms confined in optical lattices are a powerful platform for quantum simulation of complex many-body systems. We confine spin-1/2 atomic fermions ($^6$Li) to one dimension and realize the Yang-Gaudin model, the low-energy behavior of which is expected to be that of a Tomonaga-Luttinger liquid [1]. Such liquids exhibit bosonic collective low-energy excitations and spin-charge separation. Using Bragg spectroscopy and a Feshbach resonance, we directly excite either the spin or charge wave with a tunable repulsive interaction strength. We observe the onset of spin-charge separation as interactions are increased from zero. The spin and charge excitation velocities are equal for the non-interacting case, while the charge-mode velocity increases and the spin-mode velocity decreases with increasing interaction, a hallmark of spin-charge separation. The excitation spectra provide access to the dynamic structure factors of each mode, which are in quantitative agreement with the Tomonaga-Luttinger liquid theory, including nonlinear corrections due to band-curvature and back-scattering.

[1] Ruwan Senaratne, Danyel Cavazos-Cavazos, Sheng Wang, Feng He, Aashish Kafle, Ya-Ting Chang, Han Pu, Xi-Wen Guan and Randall G. Hulet, arXiv:2111.11545 [cond-mat.quant-gas]

17:00 Symmetry-violating properties for precision measurements in diatomic molecules

High-precision experiments to measure parity (P), and parity and time-reversal (P, T) violation using paramagnetic molecules are a promising route to look for physics beyond the Standard Model of particle physics. Using close-lying opposite-parity molecular states enhances the symmetry-violating experimental signals. This enhancement is purely relativistic and increases with the atomic number [1], making systems containing heavy atoms ideal for symmetry-violation experiments. The enhancement factor can not be measured separately and therefore electronic structure theory is needed to determine its value. This work presents the molecular enhancement for the nuclear spin-dependent P-violating anapole moment in the diatomic molecules containing lanthanum and lutetium heavy atoms. We employ the finite field approach with the relativistic 4-components coupled-cluster method in the DIRAC program [2]. In addition, we present the enhancements factor for the P, T–violating electron electric dipole moment, the P, T–violating electron-nucleus interaction, and the P, T–violating nuclear magnetic quadrupole moment. We pursue a systematic study to estimate the effect of various computational parameters, such as the basis set and electron correlation, on the calculated properties. We have found a consistent dependence of the different symmetry-violating properties on the computational parameters leading to similar uncertainties. The precision of our calculations is approximately 6% and makes the reported enhancement factors suitable for extracting the relevant fundamental properties from future measurements.

References

[1] Bouchiat M.A., Bouchiat C.C. Journal de Physique (1974), 35, 899-927.

[2] Saue T, Bast R, Gomes AS, et al. The Journal of chemical physics (2020), 152, 204104.

17:00 Synthetic Dimensions of Trap States in cold atoms

I will report on the first realisation of a very long and controllable synthetic dimension of atomic harmonic trap states [1]. To create this, we couple trap states by dynamically modulating the trapping potential of the atomic cloud with patterned light. By controlling the detuning between the frequency of the driving potential and the trapping frequency, we implement a controllable force in the synthetic dimension. This induces Bloch oscillations in which atoms move periodically up and down tens of atomic trap states. We experimentally observe the key characteristics of this behaviour in the real space dynamics of the cloud, and verify our observations with numerical simulations and semiclassical theory. This experiment provides an intuitive approach for the manipulation and control of highly-excited trap states, and sets the stage for the future exploration of topological physics in higher dimensions. I will also report on the realization and characterisation of optical potentials for ultracold atoms using a superluminescent diode [2]. The light emitted by this class of diodes is characterised by high spatial coherence but low temporal coherence. On the one hand, this implies that it follows Gaussian propagation similar to lasers, allowing for high intensities and well-collimated beams. On the other, it significantly reduces those interference effects that lead to severe distortions in imaging.
[1] arXiv:2112.10648
[2] arXiv:2109.05096

Speaker: Aaron Smith (The University of Birmingham)

17:00 The integration of 2D atomic arrays with photonic crystal waveguides

Arrays of neutral atoms offer a promising platform for building controllable and scalable quantum many-body systems. Atoms of the same species have identical transitions and are practically unlimited in supply. Given the maturity of the field of atomic physics, a large toolbox of advanced techniques for cooling and manipulating atoms is available. Atoms in ultra-high vacuum systems are also decoupled from their environment, allowing for long coherence- and lifetimes. However, this strong decoupling poses a challenge for coupling atoms with one another.

We seek to couple atoms via the exchange of optical photons. However, it is generally difficult to achieve strong coupling between atoms and light, propagating in free space, at the single particle level. Moreover, the spontaneous emission of light from an atom into free space is isotropic, further limiting the interaction strength. Based on pioneering work[1,2], our goal is to engineer strong atom-atom interactions mediated by light, in a 2D setting. By trapping atoms near carefully designed photonic crystals, the light emitted by the atoms couples strongly to the crystal.

The light guided by the photonic crystals can be highly confined, allowing for much stronger light-matter coupling than in free space. Given the discrete symmetries of the photonic crystal, the mode of the guided light will be highly directional, offering the opportunity to engineer specific interactions depending on the location of the atoms with respect to one another. This allows one to implement different Hamiltonians for simulating quantum systems such as 2D Ising-like systems, as seen in quantum magnetism[3].
We report on our progress towards trapping 2D arrays of individual Cesium atoms using optical tweezers, near a 2D dielectric structure. Using a dual compartment vacuum system, we transfer cold Cesium atoms from a source chamber to a science chamber, containing a photonic crystal. Here, the atoms are recaptured and subsequently trapped in optical tweezers.
[1]: A. González-Tudela, C. L. Hung, D. E. Chang, J. I. Cirac, H. J. Kimble, Nat. Photon. 9, 320 (2015)
[2]: Xingsheng Luan, Jean-Baptiste Béguin, Alex P. Burgers, Zhongzhong Qin, Su-Peng Yu, Harry J. Kimble, Adv. Quantum Technol. 3, 2000008 (2020).
[3]: D. E. Chang, J. S. Douglas, A. González-Tudela, C.-L. Hung, H. J. Kimble, Rev. Mod. Phys. 90, 031002

17:00 Toward the realization of single quantum impurities in a new ultracold ytterbium experiment

Ultracold atoms provide a unique playground for exploring many-body phenomena emerging in strongly correlated systems, owing to an exceptional control over Hamiltonians, their long coherence times, and recently established single-atom microscopy techniques. Here, I will report on the ongoing development of a new atom experimental apparatus in Trieste, aiming to control and detect ytterbium atoms at the single-particle level. Ytterbium presents several features which make it ideal to investigate open questions in problems based on quantum impurity systems. Manipulating the external and internal degrees of freedom of individual atoms by optical tweezer microtraps, and exploiting the precise toolbox of two-electron-atom clock spectroscopy, we aim at coherently manipulating individual, localized impurities interacting with a many-particle medium, triggering and observing their dynamics with interferometric techniques. This will allow to shed light on important questions, such as the ultrafast response and the formation of Kondo resonances in Fermi systems, as well as the competition between quantum dephasing and thermal decoherence therein.

17:00 Towards a compound $^{27}$Al$^+$ - $^{40}$Ca$^+$ and multi-ion $^{40}$Ca$^+$ clock

An optical atomic clock based on a single aluminum ion is holding the current world record for accuracy with a fractional frequency uncertainty below $10^{-18}$ [1]. This outstanding precision allows for novel applications like relativistic geodesy [2,3] on the cm level and helps to tighten the bounds for physics beyond the standard model [4]. But single ion clocks are impeded by their low signal-to-noise ratio and require therefore long averaging times. These can be significantly reduced by probing at the coherence time limit of the atom, given by the excited state lifetime. However, such second-long probe times can only be achieved with lasers offering correspondingly long coherence time.
Here we present the current status of PTB’s laboratory aluminum ion clock and the experimental implementation of a multi-ion Ca$^+$ reference based on dynamical decoupling to extend the clock laser coherence time in the future.
We present the estimated error budget of the $^{27}$Al$^+$ clock based on calibration measurements using a $^{40}$Ca$^+$ ion as a sensor. This includes characterization of black body radiation, residual kinetic energy from excess micromotion as well as second order and ac Zeeman shifts caused by dc magnetic fields and magnetic fields from the trap drive, respectively. Recent upgrades of the vacuum system improved the estimated accuracy to $1.1 \times 10^{-18}$.
Improving the signal-to-noise ratio of the clock interrogation requires increasing the number of stored ions or longer interrogation times. We present a continuous dynamic decoupling scheme [5] to suppress inhomogeneous broadening by quadrupole and tensor ac Stark shifts in multi-ion $^{40}$Ca$^+$ crystals. Simultaneous suppression of first order Zeeman shifts allows interrogation of the crystal close to the natural lifetime limit. A clock laser pre-stabilized to a multi-ion $^{40}$Ca$^+$ reference will extend the laser coherence time and enable seconds long interrogation of $^{27}$Al$^+$ in the future, thus forming a compound clock.

[1] S. M. Brewer, J.-S. Chen, A. M. Hankin, E. R. Clements, C. W. Chou, D. J. Wineland, D. B. Hume, and D. R. Leibrandt, $^{27}$Al$^+$ Quantum-Logic Clock with a Systematic Uncertainty below $10^{-18}$, Phys. Rev. Lett. 123, 033201 (2019).
[2] W. F. McGrew et al., Atomic Clock Performance Enabling Geodesy below the Centimetre Level, Nature 564, 87 (2018).
[3] T. E. Mehlstäubler, G. Grosche, C. Lisdat, P. O. Schmidt, and H. Denker, Atomic Clocks for Geodesy, Rep. Prog. Phys. 81, 064401 (2018)
[4] M. S. Safronova, D. Budker, D. DeMille, D. F. J. Kimball, A. Derevianko, and C. W. Clark, Search for New Physics with Atoms and Molecules, Rev. Mod. Phys. 90, 025008 (2018).
[5] N. Aharon, N. Spethmann, I. D. Leroux, P. O. Schmidt, and A. Retzker, Robust Optical Clock Transitions in Trapped Ions Using Dynamical Decoupling, New J. Phys. 21, 083040 (2019).

17:00 Towards a continuous wave superradiant calcium laser

Superradiant lasers are suitable as light sources with an ultranarrow linewidth. Superradiant emission can exhibit a linewidth, which is narrower than the natural decay on the same transition [1]. Like conventional lasers, superradiant lasers usually incorporate a cavity to mitigate the atom-light interaction. In the conventional case the emission frequency is strongly dependent on the cavity and therefore sensitive to mechanical perturbations. However, for superradiant lasers operating in the bad-cavity regime, this dependance is highly suppressed [2]. This makes superradiant Lasers operating on ultranarrow transitions, as the alkaline-earth metal clock transitions, ideal candidates for oscillators of next generation atomic clocks.
Currently, our experiment loads cold calcium-40 atoms from a magneto optical trap into a one-dimensional optical lattice prepared inside a cavity. By incoherent population of the metastable triplet state, pulsed superradiant emission on the intercombination line was realized. Due to the incoherent preparation of the atomic sample, it was also possible to show the spontaneous nature of the superradiant pulses and measure a delay distribution [3].
At present, the setup is being extended by an incoherent repumping mechanism, which will allow limited time continuous wave operation.

[1] Meiser, Dominic, et al. "Prospects for a millihertz-linewidth laser." Physical Review Letters 102.16 (2009): 163601.
[2] Norcia, Matthew A., and James K. Thompson. "Cold-strontium laser in the superradiant crossover regime." Physical Review X 6.1 (2016): 011025.
[3] Laske, Torben, Hannes Winter, and Andreas Hemmerich. "Pulse delay time statistics in a superradiant laser with calcium atoms." Physical Review Letters 123.10 (2019): 103601.

17:00 Towards nano-structured potentials: coupling of an ultra cold atomic gas with a surface and sub-wavelength imaging.

Cold atoms in lattices have appeared as good candidates to mimic the properties of electrons in solid-state systems and to simulate quantum materials. However, experimental techniques currently use optical lattices in the far-field. This limits the lattice spacing to λ/2 and gives an upper bound to the relevant energy scale (tunneling and interaction), making it difficult to enter deeply into the proper quantum regimes to observe magnetic quantum correlations or strongly correlated phases. Our project aims at reducing the lattice period to bridge the gap between solid-state (Å) and far-field lattice (500nm) by developing a hybrid quantum system of Bose and Fermi quantum gas in close proximity of a nanostructured surface generating sub-wavelength lattice potentials. To push toward this goal, we have developed a novel method to transport and trap an ultracold atomic cloud in the vicinity of a surface. In this poster, we will discuss the design of the first atom-chip that will implement this method, and report on tests about the transport sequence. In particular, by measuring the power spectral density of the trap parameters, we predict the noise-induced heating of the trapped cloud. Subwavelength lattice analysis requires addressing each site individually with a resolution better than the diffraction limit. For that purpose, we implemented a tunable sub-wavelength imaging system with a theoretical resolution of 30nm and we demonstrated its performance by resolving the wave-packet of a cloud in a single lattice site. This scheme involves two superimposed optical lattices at 1064nm and 1529nm, whose interfringe can be tuned. In the poster, the experimental setup will be presented, and the data will be compared to the theoretical expectation.

17:00 Towards the creation of ultracold, neutral plasmas with oppositely charged particles of equal mass via long-range Rydberg molecules

Long-range Rydberg molecules are molecules in highly-excited electronic states where the binding results from the scattering of an almost free electron of a neutral atom within its orbit. In our lab, we have in recent years developed a detailed experimental and theoretical understanding of the binding in homo- and heteronuclear long-range Rydberg molecules [1]. Our experimental techniques include high-resolution photoassociation and millimeter-wave spectroscopy in ultracold atomic mixture spectroscopy. A novel, especially insightful tool is photodissociation spectroscopy of long-range Rydberg molecules, which allows for a tomographic characterization of the molecular electronic and vibrational state [2].
In this presentation I will focus on our recent progress towards the creation of an ultracold plasma consisting of Cs$^+$ ions and Cs$^-$ ions [3]. Our experimental route starts with the photoassociation of long-range Rydberg molecules from an ultracold gas of ground-state atoms using a single-photon UV excitation. These molecules are then deexcited to ion-pair states, also called heavy Rydberg molecules, by nanosecond-long pulses from a mir-IR laser. Products are characterized by time-of-flight mass spectrometry. The dense gas of ultracold molecules in ion-pair states forms an ideal starting point to form an ultracold neutral plasma, e.g. by RF dissociation.

[1] M. Peper and J. Deiglmayr, Heteronuclear Long-Range Rydberg Molecules, Phys. Rev. Lett. 126, 013001 (2021)
[2] M. Peper and J. Deiglmayr, Photodissociation of Long-Range Rydberg Molecules, Phys. Rev. A 102, 062819 (2020)
[3] M. Peper and J. Deiglmayr, Formation of Ultracold Ion Pairs through Long-Range Rydberg Molecules, J. Phys. B: At. Mol. Opt. Phys. 53, 064001 (2020)

17:00 Ultrafast Rydberg experiments with ultracold atoms in optical tweezers

Rydberg atoms, with their giant electronic orbitals, exhibit dipole-dipole interaction reaching the GHz range at a distance of a micron, making them a prominent contender for realizing ultrafast quantum operations. However, such strong interactions between single atoms have never been harnessed so far because of the stringent requirements on the fluctuation of the atom positions and the necessary excitation strength. Here, we introduce novel techniques to explore this regime [1]. First, we trap and cool atoms to the motional quantum ground-state of holographic optical tweezers allowing to control the inter-atomic distance down to 1.5 µm with a quantum-limited precision of 30 nm. Then, we use ultrashort laser pulses to excite a pair of these close-by atoms to a Rydberg state simultaneously, far beyond the Rydberg blockade regime [2], and perform Ramsey interferometry with attosecond precision. This allows us to induce and track an ultrafast interaction-driven energy exchange completed on a timescale of nanoseconds, two orders of magnitude faster than in any other Rydberg experiments with individual atoms. This ultrafast coherent dynamic gives rise to a conditional phase which is the key resource for a quantum gate, opening the path for quantum simulation [2] and computation operating at the speed-limit set by dipole-dipole interactions with this ultrafast Rydberg platform.

[1] Y. Chew et al., arXiv: 2111.12314
[2] V. Bharti et al., arXiv : 2201.09590

17:00 Universal Properties of Anisotropic Dipolar Bosons in Two Dimensions

The energy of ultra-dilute quantum many-body systems is known to be a
universal function of the gas parameter $x = n a_0^d$, where n is the density,
a0 the s-wave scattering length, and d the dimensionality of the space (d =
1, 2, 3) [1]. The universal regime typically holds only at small x and
extends up to values no larger than 0.001 [2,3]. Beyond that point, specific
details of the interaction start to be relevant, and different interactions
with the same s-wave scattering length lead to different predictions. Dipolar
systems are peculiar in this regard since the anisotropy of the interaction
makes a0 depend on the polarization angle α, in such a way that different
combinations of n and α value of the gas parameter x [4]. In this work we
analyze the scaling properties of a system of polarized dipolar bosons in two
dimensions as a function of the density and polarization dependent scattering
length, up to very large values of x. We study the energy per particle and
main structural properties of the ground state as a function of the density and
scattering length at fixed gas parameter. We find that the dipolar
interaction shows relevant scaling relations up to unusually large values of
x that hold almost to the boundaries in the phase diagram where a transition
to a stripe phase takes place. The impact of the anisotropy of the interaction
in this context is also analyzed.

[1] T.D. Lee and C.N. Yang, Phys. Rev. 105, 1119 (1957)
[2] F. Mazzanti, A. Polls, and A. Fabrocini, Phys. Rev. A67, 063615, (2003).
[3] S. Giorgini, J. Boronat, and J. Casulleras, Phys. Rev. A60, 5129 (1999).
[4] A. Macia, F. Mazzanti, J. Boronat, and R. E. Zillich, Phys. Rev. A84,
033625 (2011).

17:00 What Does Entanglement Sudden Death Require?

Vacuum is one of the most interesting phenomena of the real world. A two-level atom, frequently treated as a qubit, when unavoidably touched by vacuum, is unstable on its excited level, even if it does not interact with any other system. All states except the ground state suffer from decay due to interaction with vacuum radiation modes. The atom falls to the ground state in asymptotic time and a photon is emitted, a process known as spontaneous decay.

The situation becomes more interesting when multiple atoms are present and placed far apart, such that they can be considered as sitting in distinguishable vacuum states. As in the single-atom case, the excited elements of the multi-atom density matrix decay exponentially to zero. However, previous results of Yu and Eberly [Science 323, 598 (2009)] have shown that two-atom entanglement (also called nonseparability) has a transition to zero in such systems that is temporally abrupt. Such dynamics of entanglement is non-analytic, and this bizarre behaviour is usually termed entanglement sudden death (ESD).

It is then natural to ask how entanglement among more than two qubits behaves when the qubits decay independently in their respective cavities. Are there also sudden transitions in these more complicated systems? Specifically, what is the requirement for ESD in these systems? These open questions are made difficult by the following two obstacles. First, existing entanglement measures cannot quantify the degree of genuine multipartite entanglement (GME), the measure of the entanglement resource that plays a central role in quantum information and communication tasks such as the three-qubit quantum teleportation. Second, even if a GME measure is used, it is an extremely difficult task to evaluate it for general mixed states, which are ubiquitous for vacuum decay.

In this work, we provide solutions to the above two problems. For the GME measure, we use our recently developed pure-state measure Concurrence Fill, which was proven to detect genuine tripartite entanglement [see Xie and Eberly, Phys. Rev. Lett. 127, 040403 (2021)]. For the mixed-state issue, we avoid deriving an analytic formula, which is currently impossible. Instead, we apply a previous result to convert the evaluation of mixed-state entanglement into a practical numerical task [Eisert, Brandão, and Audenaert, New J. Phys. 9, 46 (2007)].

With these methods, we study the entanglement dynamics for three-qubit systems, wherein each qubit interacts with its own vacuum environment via the amplitude-damping channel. We numerically examine the dynamics of the Concurrence Fill measure of genuine tripartite entanglement among the three qubits, when different initial three-party states are selected.

Specifically, when the initial state is the generalized GHZ state, $|\text{GHZ}\rangle=\cos\theta|eee\rangle+\sin\theta|ggg\rangle$, where $|e\rangle$ and $|g\rangle$ are the excited and ground states for each atom, ESD occurs when the amplitude of the all-excited state $|eee\rangle$ exceeds a threshold value. Furthermore, we show that ESD does not occur if the initial state is the singly-excited $W$ state, $|W\rangle=(|egg\rangle+|geg\rangle+|gge\rangle)/\sqrt{3}$, or the doubly-excited $\overline W$ state, $|\overline W\rangle=(|gee\rangle+|ege\rangle+|eeg\rangle)/\sqrt{3}$.

These observations imply that when the three-qubit initial state is pure, the presence of the all-excited $|eee\rangle$ state is a necessary requirement for ESD to occur, despite the fact that $|eee\rangle$ is a product state which cannot exhibit ESD alone. To test this novel conjecture, we consider as the initial state the superposition of $|eee\rangle$ with the no-ESD $|W\rangle$ state, $|S\rangle=\cos\theta|eee\rangle+\sin\theta|W\rangle$. In agreement with our conjecture, ESD occurs when the amplitude of $|eee\rangle$ exceeds a threshold value. Our results bring new insights toward a more complete understanding of entanglement sudden death.

Tuesday 19 July

08:00 → 08:45 Exhibitors: Exhibitor Show Hours 8am-5:30pm

Exhibitors and vendors available

08:00 → 08:45 Registration / Info Desk open 8am - 5:30pm

08:45 → 10:30 Plenary session

10:30 → 11:00 Coffee Break

11:10 → 12:20 Plenary session

14:00 → 15:10 Plenary session

15:10 → 15:40 Break

15:50 → 17:00 Plenary session

17:00 → 18:30 Poster session: Tuesday

17:00 A cold and slow beam of CH radicals for laser cooling and trapping experiments

Techniques to directly laser cool and trap molecules at ultracold temperatures have revealed a new path towards the full quantum control of a diverse range of species with a variety of internal structures. Our experiment will capitalize on this generality by directly laser cooling and trapping CH radicals for tests of ultracold organic chemistry. The low mass and blue optical transitions in this species lead to high recoil velocities which can significantly reduce the photon budget and rovibrational closure needed to slow, cool and trap a molecular beam from our cryogenic source. Here we will present the latest results characterizing our slow molecular beam and probing the chemistry of CH radicals at ~1 K.

*This work is supported by the AFOSR and the University of Connecticut, including a Research Excellence Award from the Office of the Vice President for Research.

17:00 A modified variational method for a quantum gas in a constrained surface

Confined quantum gases in a toroidal-like potential can be studied by a variational method using the like-Gross-Pitaevskii equations. The variational approach determines the dynamics of the quantum cloud, as the evolution of the aspect ratio during the free expansion of the cloud and the collective modes. We adapted the variational method to parametrize on a curved surface and effective dynamics. We use the thin-layer quantization scheme, focusing on three-dimensional surfaces, thus resorting to the Schrödinger equation for a particle with constrained dynamics to a curved surface. We propose a hybrid Lagrangian density and split the wave function into two parts: the normal and a tangential component to the surface that allow us to study the system through the extension of the variational method. Finally, we obtain the equations of motion that describe the dynamics separately in the normal and tangential parts on the surface.

17:00 A novel trapped-ion quantum computer using optical tweezers and electric fields

Trapped-ions are one of the most mature platforms for quantum computation and quantum simulation. In trapped-ion quantum simulators the spin-spin interactions are mediated by the collective motion of the ions in the crystal (phonons). We show that additional optical tweezer potentials can be used to engineer the phonon spectrum, and thus tune the interactions and connectivity of the ion qubits beyond the power-law interactions accessible in current setups [1].

Moreover, we use optical tweezers to create two new scalable architectures for trapped-ion quantum computing. Neither scheme relies on ground state cooling or the Lamb-Dicke approximation. In the first we use a combination of optical tweezers delivering qubit state-dependent local potentials with an oscillating electric field [2]. Since the electric field allows for long-range qubit-qubit interactions mediated by the center-of-mass motion of the ion crystal alone, it is inherently scalable to large ion crystals. In the second scheme, the strong curvature of the light field of the tightly focused tweezer creates strong polarization gradients that lead to qubit-state dependent forces on the ion (optical Magnus effect [3]). We show that these may be used to implement quantum logic gates on pairs of ion qubits in a crystal [4].

[1] Phys. Rev. A 104, 013302 (2021)
[2] Phys. Rev. Lett. 127, 260502 (2021)
[3] Phys. Rev. Lett. 125, 233201 (2020)
[4] In preparation.

17:00 A performance bound for quantum thermal machines

Out-of-equilibrium atomic systems may be used to develop quantum thermal machines which operate continuously at steady state. At such small scales, the energy currents characterizing work and heat exchange with thermal reservoirs exhibit fluctuations large enough to play a significant role in evaluating machine performance. I introduce here a novel set of bounds on the performance of steady-state quantum thermal machines which involve the fluctuations in their input and output energy currents. Namely, the ratio of a machine's output to input fluctuations is bounded from below by the square of its efficiency, and from above by the square of the relevant Carnot bound. This leads to a tighter-than-Carnot bound on the efficiency itself. I will describe a model-independent proof of these results for systems near equilibrium. I will also discuss efforts to extend these results to the far-from-equilibrium regime, in the context of the quantum absorption refrigerator: a paradigmatic model for a thermal machine which can be realized using atomic systems.

17:00 A programmable quantum simulator with two-electron Rydberg atoms in optical tweezer arrays

I will present a new programmable quantum simulator based on Rydberg strontium atoms trapped in optical tweezers arrays at CNR-INO and LENS in Florence. This new experimental setup, supported by an infrastructural program of CNR, is now under construction in our laboratories as a joint effort of CNR and the University of Florence.
I will present the main features of the apparatus, including the techniques that will be employed for the generation of programmable arrays of optical tweezers and for the control of the different sources of decoherence. I will also discuss the advantages offered by two-electron atoms, including narrow optical transitions that can be exploited for effective atomic cooling schemes, and the existence of a metastable state that provides an additional degree of freedom for the manipulation of individual atoms, as well as a direct connection to frequency metrology. I will finally discuss the applications that we envision for this new setup, in particular the simulation of quantum spin models with different types of interactions and topologies, and the realization of multi-particle entangled states.

17:00 A simplified cold Sr experiment for cavity-based quantum simulation

We have developed a relatively simple and compact Sr experiment designed for cavity QED with Sr atoms in a miniature ring resonator. The vacuum setup has a total length of 40cm including oven, Zeeman slower and glass cell, and routinely produces 2x10^7 87Sr atoms in the MOT with an oven temperature of 440°C. The slower does not require magnetic coils on its own as it exploits the far field of appropriately designed MOT coils, further reducing complexity and power consumption. The laser system uses master-slave architecture throughout and does not require SHG or other high-power lasers.

We also present first results on the optical properties of a miniature ring cavity with laser-machined mirrors that will be used in this experiment.

Speaker: Jakob Reichel (Laboratoire Kastler Brossel)

17:00 A single cold atom as a single-photon detector.

Single ions and atoms are interesting systems for single-photon detection due to their frequency selectivity and very low dark counts [2,3]. These capabilities are useful for any application in which a very low power signal must be detected against a broadband background. An example of such an application would be free-space quantum communication in daylight.
In this work, we present and describe the operation of a quantum jump photodetection (QJPD) technique for measuring single photons using a single neutral 87Rb atom in a strongly-focused optical dipole trap [4,5]. We report results of first-principles calculations for the main dark count contributions: spontaneous Raman transitions driven by readout light (which can be avoided by separating the detection and readout time windows) and spontaneous Raman transitions driven by trap light (which is unavoidable but gives dark count rates two orders of magnitude below that state of the art single-photon detectors). We quantify the frequency selectivity with the \textit{equivalent noise bandwidth}, which we find is up to two orders of magnitude narrower than the best atomic filters. Preliminary experimental results for these figures of merit in a ``Maltese cross'' atom trap will be presented.

1[Quantum-Jump Photodetection technique for a single neutral 87Rb atom in a free-space dipole trap. a) Relevant energy levels and lights used in the experiment. Cooler light (orange) for preparation and readout in the closed transition and signal light (purple) that will be measured. b) Measurement sequence. First cooler pulse prepares atom in the dark ground state (F=1), signal pulse causes a quantum jump to the bright state (F=2), readout pulse causes sudden fluorescence if the atom jumped and then reprepares the atom in the dark state. c) Counts as a function of time for a detection event. The sudden increase in fluorescence counts due to the atom cycling in the closed transition after a jump creates a well-above background peak that can be used for counting detections.][2]

[2] C. Kurz, et al., Phys. Rev. A 93, 062348 (2016)
[3] N. Piro, et al. Nature Phys 7, 17–20 (2011)
[4] N. Bruno, et al., Opt. Express 27, 31042-31052 (2019).
[5] L. Bianchet, et al., Open Res Europe, 1:102 (2021).

17:00 A transportable cold atom accelerometer for inertial navigation

Many sectors of society and the economy are now heavily reliant on Global Navigation Satellite Systems (GNSS). However, GNSS has several underlying vulnerabilities and cannot be used under- water or underground. In these situations, Inertial Navigation Systems (INSs) can act as a reliable alternative. These self-contained devices reconstruct the trajectory of a vehicle being tracked by measuring its acceleration and rotation rate. A complete INS combines measurements from three orthogonal accelerometers and three orthogonal gyroscopes. Together with knowledge of the vehicle’s starting position, its current location can be calculated, without the need for an external reference. Conventional systems use high precision classical sensors, however long-term performance is currently limited by scale factor and bias drifts.
With their high-accuracy and long-term stability, cold atom interferometers have the potential to substantially improve long-range inertial navigation. At Imperial College, we are developing such systems for use in quantum enhanced INSs. Clouds of rubidium-87 atoms are cooled to ultra-cold temperatures then split, reflected, and recombined using stimulated Raman transitions to make an atom interferometer for inertial sensing.
Here, we describe our recent work developing a ruggedised quantum accelerometer for navigation. Our new system contains the laser for cooling and trapping atoms and driving Raman transitions, a science chamber for atom interferometry, and all the electronics and control systems, packaged into a transportable system for deployment outside the laboratory.

17:00 Accurate and complete atomic data set for Cd XLVII

Atomic data have received a great deal of attention, due to their need for the upcoming ITER project (International Thermonuclear Experimental Reactor). So, extensive spectroscopic studies both experimental and theoretical have been performed in the last years in order to estimate the power loss from the impurities in the forthcoming fusion reactors. Accurate values of wavelengths and their errors are required for interpretation of a wealth of high-resolution data obtained in the last two decades by the Chandra X-ray Observatory and the European Space Agency’s X-ray Multi-Mirror Mission [1].

As previously published [2, 3, 4, 5, 6, 7], we continue to focus on He-like ions. Energy levels, wavelengths, weighted oscillator strengths, transition probabilities and lifetimes are calculated for all levels of 1s2 and 1snl (n = 2−6) configurations of He-like cadmium ion.

The calculations were carried out using the GRASP2018 code based on the multiconfiguration Dirac-Hartree-Fock (MCDHF) [8]. Transition probabilities are reported for all types of transitions (E1, E2, M1 and M2 transitions). Breit interactions and quantum electrodynamics effects are included in the RCI calculations. Comparisons were made with other data found in the literature and a good agreement was found which confirms the reliability of our results. We identified some new data that are calculated for the first time. This computational approach enables us to present a consistent and improved data set of all important transitions of the Cd XLVII spectrum, which are useful for identifying transition lines in further investigations.

References
[1] V. A. Yerokhin and A. Surzhykov, J. Phys. Chem. Ref. Data 48 (2019) 033104.
[2] D. E. Salhi and H. Jelassi, Canadian Journal of Physics 96 (2017) 3.
[3] D. E. Salhi and H. Jelassi, Orient. J. Phys. Sciences. 2 (2017) 2.
[4] D. E. Salhi, P. Quinet and H. Jelassi, Atomic Data and Nuclear Data Tables 126 (2019) 70-157.
[5] D. E. Salhi, S. Ben Nasr and H. Jelassi, Radiation Physics and Chemistry 177 (2020) 108817.
[6] D. E. Salhi, S. Ben Nasr, S. Manai, H. Jelassi, Results in Physics 23 (2021) 103960.
[7] S. Manai, D. E. Salhi, S. Ben Nasr and H Jelassi, Results in Physics 37 (2022) 105487.
[8] C. Froese Fischer, G. Gaigalas, P. Jonsson, J. Bieron, Computer Physics Communications 237 (2019) 184.

17:00 An Experiment to Measure the Electron's Electric Dipole Moment Using an Ultracold Beam of YbF Molecules

The standard model predicts that the electron’s electric dipole moment (eEDM, $d_e$) is too small to measure with current technology [1]. Theories that extend the standard model, however, predict much larger values, often exceeding $10^{-29}~e~\text{cm}$. With the current experimental upper limit set at $|d_e| < 1.1 \times 10^{-29}~e~\text{cm}$, [2] we can expect that improved measurements will either discover new physics or rule out most of the remaining parameter space for popular theories beyond the standard model. Measurements of $d_e$ are made by measuring the precession of the electron spin induced by an applied electric field. The precession angle is enhanced when the electron is bound to a heavy polar molecule. The precision can be further improved by increasing the spin precession time and the total number of molecules detected. To this end, we have produced an intense beam of laser-cooled YbF molecules [3] and built an experiment to measure $d_e$ using this beam [4]. The laser cooling lowers the temperature below $100~\mathrm{\mu K}$ and increases the beam brightness by at least a factor of 300, leading to a projected statistical sensitivity better than $10^{-30}~e~\text{cm}$. Realising such high precision requires a spin precession region with exceptionally low magnetic noise. Our apparatus features ceramic electric field plates inside a glass vacuum chamber, minimising magnetic Johnson noise, a four-layer magnetic shield with a shielding factor exceeding $10^6$, and an array of atomic magnetometers. The magnetic noise in the apparatus is below $50~\mathrm{fT} /\sqrt{\mathrm{Hz}}$ at 1 Hz. The poster will present our progress in laser cooling YbF molecules and our characterisation and optimisation of the eEDM apparatus.

[1] M. Pospelov and A. Ritz., CKM benchmarks for electron electric dipole moment experiments., Phys. Rev. D, 89, 056006, (2014).
[2] V. Andreev et al., Improved limit on the electric dipole moment of the electron., Nature, 562, 355–360, (2018).
[3] X. Alauze et al., An ultracold molecular beam for testing fundamental physics, Quantum Sci. Technol., 6, 044005, (2021).
[4] N. J. Fitch, J. Lim, E. A. Hinds, B. E. Sauer, and M. R. Tarbutt., Methods for measuring the electron’s electric dipole moment using ultracold YbF molecules, Quantum Sci. Technol., 6, 014006, (2021).

17:00 Atmospheric channel measurements for long-range optical time transfer and quantum state dissemination

Free-space optical time transfer is a key enabling technology for intercontinental comparisons of optical atomic clock time scales and the eventual redefinition of the SI second. However, full realization of their potential for femtosecond-level intercomparisons requires ground-to-space (and possibly space-to-space) link operation. We present a series of long-range atmospheric channel characterizations and time transfer demonstrations, through a variety of atmospheric turbulence conditions. In addition to time transfer, our channel measurements are also relevant for long-range quantum communications, including space-to-ground quantum resource dissemination.

---

Approved for public release; distribution is unlimited. Public Affairs release approval AFRL-2022-2073.

17:00 Atomic arrays driven by broadband squeezed light

In this theoretical work we describe the evolution of an atomic array driven by broadband squeezed light. Photons in a squeezed field are created as correlated pairs, thus leading to a phase-sensitive amplification and deamplification of fluctuations. These fluctuations depend on the squeezing mechanism and the spatial structure of the modes carrying the correlated pairs [1-3]. By spreading several atoms within this environment, we are able to probe the local structure of the field at different points and study its underlying temporal and spatial correlations. We show that, like the squeezed source illuminating them, atoms correlate in pairs to form a collective state that disentangles from its environment. Being detached from the environment, atoms become trapped in this state, thus increasing the purity of the system as time advances. For this to happen, however, atoms have to be placed at points where the correlations of the field are maximized. We explore these points and discuss the steady states formed outside of them.

This work builds upon a recent trend where the collective radiation of atomic ensembles is used as a tool to extend the standard theory of quantum optics to account for both spatial and temporal correlations of light.

[1] C. W. Gardiner, Phys. Rev. Lett. 56, 1917 (1986).
[2] H. J. Carmichael, A. S. Lane, and D. F. Walls, Phys. Rev. Lett. 58, 2539 (1987).
[3] K. W. Murch, S. J. Weber, K. M. Beck, E. Ginossar, and I. Siddiqi, Nature 499, 62 (2013).

17:00 Atomic spin-controlled non-reciprocal Raman amplification of fibre-guided light

In a non-reciprocal optical amplifier, gain depends on whether the light propagates forwards or backwards through the device. Typically, one requires either the magneto-optical effect, a temporal modulation, or an optical nonlinearity to break reciprocity. By contrast, here, we demonstrate non-reciprocal amplification of fibre-guided light using Raman gain provided by spin-polarized atoms that are coupled to the nanofibre waist of a tapered fibre section [1]. The non-reciprocal response originates from the propagation direction-dependent local polarization of the nanofibre-guided mode in conjunction with polarization-dependent atom-light coupling. We show that this novel mechanism can also be implemented without an external magnetic field and that it allows us to fully control the direction of amplification via the atomic spin state. Our results may simplify the construction of complex optical networks. Moreover, using other suitable quantum emitters, our scheme could be implemented in photonic integrated circuits and in circuit quantum electrodynamics.

[1] S. Pucher, C. Liedl, S. Jin, A. Rauschenbeutel, P. Schneeweiss
Atomic spin-controlled non-reciprocal Raman amplification of fibre-guided light
Nature Photonics 16, 380 (2022)

17:00 Benchmarking a large-scale quantum simulator with useful applications

Using a Rydberg atom-array quantum simulator, we experimentally demonstrate new applications which become possible through verifiable quantum evolution. At the outset, we show experimental benchmarking of system sizes with up to 60 atoms, and demonstrate new techniques in approximate verification beyond the classical simulation threshold. Further, we show how such benchmarking allows us to perform in situ local Hamiltonian learning, to optimize Hamiltonian engineering for preparing interesting quantum states, and to make quantitative comparisons between analog and digital quantum devices aiming to create maximum entanglement entropy states. These developments showcase practically useful applications for device benchmarking protocols in quantum devices, and further demonstrate concrete steps towards quantum advantage with a near term quantum simulator.

17:00 Binary collisions between quantum droplets: role of the Weber number

A theoretical analysis of the low energy surface excitations of quantum droplets formed by binary mixtures of ultracold dilute Bose gases is performed. Reliable expressions for the surface tension of the droplets are introduced based on the Thouless variational theorem. The Weber number can then be calculated as a measure of the relative importance of the inertia of the fluid in terms of the kinetic energy compared to its surface tension. By numerically evaluating the evolution of the droplets under the extended Gross-Pitaevskii equation, several regimes on the outcomes of frontal collisions of quantum droplets are identified. They range from the coalescence of the quantum droplets to their disintegration into smaller droplets. Those regimes are shown to be directly correlated to the Weber number. The numerical simulations include atoms losses of the droplets derived from self- evaporation and three--body scattering for both homo-- and hetero--nuclear mixtures.

17:00 Collective effects in dissipative quantum cellular automata

Programming irreversible dynamical rules of cellular automata into non-unitary interactions of quantum systems appears to be a promising route to studying novel collective effects. Considering a master-equation embedding of classical cellular automata, we first investigate the unexplored area of computability aspects of Markovian quantum dynamics. We introduce a novel dynamical class of open quantum many-body systems that allows studying the interplay between computational properties and quantum effects. Strikingly, we demonstrate that computational unpredictability can coexist with quantum entanglement and that it can be studied within present experiments. Next, we present a quantum version of a probabilistic majority-voting cellular automaton to address a long-standing controversy about the existence and limits of bistable behavior in the stationary states of open quantum systems. We find the first instance of genuine bistability in such systems which is driven by the breaking of detailed balance in the non-equilibrium steady state.

17:00 Connecting Quantum Information Scrambling with Entanglement Enhanced Metrology

Understanding how and at which speed information spreads in a quantum many-body system is a fundamental and intriguing question of quantum information science. Quantum metrology harnesses quantum entanglement for enhancing the precision of atomic sensors beyond the standard quantum limit. What do these apparently different fields of quantum mechanics have in common? We experimentally show that these are actually two sides of the same coin.
On the one side, the direct experimental observation of quantum information spread, called “quantum information scrambling”, is a difficult task. An emerging tool to witness scrambling are the out-of-the-time-ordered correlators (OTOCs). OTOCs require the system to evolve backward in time after the encoding of a small portion of quantum information. On the other side, in quantum metrology, collective entangled states are characterized by their quantum Fisher information (QFI) which quantifies the sensitivity of the state to a certain perturbation.
In this work, we experimentally investigate quantum information scrambling and entanglement-enhanced metrology in a Lipkin-Meshkov-Glick (LMG) model. We show that these two fields are comparable and, in particular, we demonstrate that QFI and OTOC are equivalent.
The LMG model, as well as its time-reversal, is implemented in a cavity QED system with ultracold ytterbium atoms. The cavity field mediates an effective all-to-all interaction within the atoms, while an external RF field induces a collective rotation of atoms. Moreover, we work in the regime of the LMG model where entanglement (or quantum information scrambling) occurs exponentially fast.

17:00 Correlation spectroscopy of a planar 91-ion crystal in a novel monolithic Paul trap

The development of fully controlled quantum systems in the laboratory has seen tremendous progress in recent years. One experimental platform which has shown to allow for an excellent level of control are trapped atomic ions, stored in linear radio-frequency traps. Here, one-dimensional chains of up to several tens of ions have already been employed successfully to carry out quantum simulation tasks [1,2]. In our work we aim to scale up the number of individually controllable trapped ions for quantum simulations beyond the state of the art of ~50 particles, by using the platform of planar ion crystals stored in a linear Paul trap. In this way some scalability-related problems of long ion chains, such as high heating rates of the axial motional modes and difficulties in laser-addressing outer ions, can be circumvented.
On this poster we present our new apparatus, the centerpiece of which is a novel monolithic linear Paul trap, enabling us to trap stable 2-dimensional crystals of up to 100 40Ca+ ions. Moreover, we demonstrate our recent results on correlation spectroscopy, implemented in a planar crystal consisting of 91 ions [3]. Correlation spectroscopy is a powerful tool, initially developed in the context of precision metrology, and allows phase differences between qubits to be measured precisely even in the presence of strong correlated phase noise [4,5]. The key idea here is that due to their spatial proximity to each other in the trap the qubits, encoded in each of the 91 ions, will be affected in a collective way by noise processes such as ambient magnetic field fluctuations. Correlations in the outcomes of collective Ramsey measurements provide information about the phase differences between the qubits, even for probe times significantly longer than the coherence time of the individual particles. We apply correlation spectroscopy to characterize a magnetic field gradient, which gives rise to transition frequency differences across the planar ion crystal. In the context of measurement uncertainties, we are able to show that considering N-qubit correlations reduces the phase uncertainty with respect to 2-qubit correlations, and the advantage of using entangled states becomes negligible for N→∞.
[1] C. Kokail, C. Maier, R. van Bijnen, T. Brydges, M. K. Joshi, P. Jurcevic, C. A. Muschik, P. Silvi, R. Blatt, C.F. Roos and P. Zoller, Self-verifying variational quantum simulation of lattice models, Nature 569, 355–360 (2019)
[2] J. Zhang, G. Pagano, P. W. Hess, A. Kyprianidis, P. Becker, H. Kaplan, A. V. Gorshkov, Z.-X. Gong and C. Monroe, Observation of a many-body dynamical phase transition with a 53-qubit quantum simulator, Nature 551, 601–604 (2017)
[3] H. Hainzer, D. Kiesenhofer, T. Ollikainen, M. Bock, F. Kranzl, M.K. Joshi, G. Yoeli, R. Blatt, T. Gefen and C.F. Roos, Correlation spectroscopy with multi-qubit-enhanced phase estimation, Preprint 2022
[4] M. Chwalla, K. Kim, T. Monz, P. Schindler, M. Riebe, C. F. Roos and R. Blatt, Precision spectroscopy with two correlated atoms. Appl. Phys. B 89, 483 (2007)
[5] C. W. Chou, D. B. Hume, M. J. Thorpe, D. J. Wineland and T. Rosenband, Quantum Coherence between Two Atoms beyond Q=1015. Phys. Rev. Lett. 106, 160801 (2011)

17:00 Correlations in the process of strong field ionization

We apply correlation function analysis for a study of strong field ionization of atoms. We show that the study of the correlations of electron's coordinate and velocity reveals patterns which can be naturally interpreted as manifestations of the electron's barrier exit point (the spatial point where the electron exits the tunneling barrier). This analysis provides an unambiguous definition of the exit point in the tunneling ionization process. The location of the exit point thus determined agrees well with the estimates used in the semiclassical simulations.

In the framework of the standard semi-classical picture of ionization based on the Keldysh theory and its modifications, known as the two-step model, an electron emerges into the continuum with zero or near zero velocity at a certain point in space (the tunnel exit), setting up initial conditions for the subsequent electron motion. An initial value of the coordinate is defined either by the so-called Field Direction Model or (for Coulomb systems) by an estimate based on the use of the parabolic coordinate system, as a point at which the electron exits the barrier. Despite the great deal of success which had the trajectory based calculations employing these initial conditions defining the subsequent electron motion, the notions of the initial conditions are not easy to reconcile with quantum mechanics (QM). We cannot assign direct meaning to the initial electron's coordinates and velocity using the wave-function provided by the solution of the conventional TDSE, such a possibility being excluded by the very basic principles of the QM. What we can do, using the TDSE and the framework of the conventional QM, is to study correlations between different observables at different moments of time. We show that study of the correlation function $C(z,t;v,t_m)$, describing correlations between the probabilities to locate electron in particular regions of the coordinate and momentum spaces, reveals patterns which can be naturally interpreted as manifestations of the electron's ionization event, providing information about spatial location of the exit point, where electron exits the tunneling barrier.

17:00 Dipolar quantum droplets and supersolids

Dipolar interactions are fundamentally different from the usual van der Waals forces in real gases. Besides the anisotropy the dipolar interaction is nonlocal and as such allows for self organized structure formation [1]. In 2015 we could observe the formation of a stable droplet crystal and found that this unexpected stability is due to beyond mean-field quantum corrections of the Lee-Huang-Yang type. When arranged in a 1D array also phase coherence between the droplets was observed, which was first evidence for a supersolid state of matter. Upon crossing the transition to the dipolar supersolid a Goldstone mode appears, which we have observed. The existence of this mode proofs the superfluid stiffness or the so-called phase rigidity of this new state of matter. We have also studied the static structure factor across the transition which allows to show that the characteristic fluctuations correspond to elementary excitations such as the roton modes, and that the supersolid state supports both superfluid as well as crystal phonons. A recent review on the discovery of quantum droplets and dipolar supersolids can be found in ref. [2].

References:
[1] review: T. Lahaye, et al., Rep. Prog. Phys. 72, 126401 (2009)
[2] review: F. Böttcher et al. Reports on Progress in Physics 84, 012403 (2021)

Speaker: T Pfau (5. Physikalisches Institut and Center for Integrated Quantum Science and Technology (IQST), Universität Stuttgart, Germany)

17:00 Efimov universalities, Bose polarons and turbulence with ultracold 39K in a 3D box trap

We present on various experiments utilizing quantum $^{39}$K gases trapped in a 3D optical box for investigations of few-body, many-body and far-from-equilibrium phenomena. The first result we present is a comprehensive characterization of F=1 manifold Feshbach resonances for magnetic fields up to 600G using loss spectroscopy and atom-dimer interferometry; these precision measurements enable us to examine Efimov and van-der-Waals universality across multiple resonances. Our second main result is the realization of a uniform system of Bose polarons. We spectroscopically probe the polaron spectral function with minimal density broadening from weak to resonant couplings, and find evidence for coherent quantum beats between repulsive polaron and an impurity-phonon bound state at strong repulsive interactions under a Ramsay protocol. As a third result, we experimentally establish an equation of state relating the energy flux to the Kolmogorov number of the turbulent cascade established under strong forcing of an interacting condensate. This equation of state is independent of the details of the driving and dissipation, independent of history, and can be rescaled into a single curve for different interaction parameters. Finally, we surprisingly demonstrate that even a shaken noninteracting condensate exhibits a self-similar scaling dynamics in momentum space with a subdiffusive energy growth, qualitatively akin to interacting turbulent behavior but quantitatively different.

17:00 Electric-field measurement in cold ion clouds

The influence of inhomogeneous electric fields in ion clouds on high-angular-momentum Rydberg states is investigated. The fields follow from a superposition of macroscopic and random microscopic (Holtsmark) fields. The ion clouds are induced experimentally by photo-ionizing cold rubidium atoms in the $5D_{3/2}$ state near the focal spot of a near-concentric 1064-nm intracavity optical lattice. We observe how the $n=57$ $F$-state mixes with the neighboring hydrogenic manifold and study evolution of spectroscopic features, such as line broadening and excitation-strength distribution for different numbers of created ions. Pump-probe experiments are performed to study the dynamics of the ion-Rydberg-atom system. Our data is utilized to evaluate the experimental feasibility of inhomogeneous-electric-field sensing with subsequent determination of the ion density. Additional experiments with Rydberg $P$-states are reported as well. Our results might be of interest for future studies of electric fields in non-neutral plasmas and in hybrid cold-atom-ion systems.

Speaker: Mr Alisher Duspayev (University of Michigan, Ann Arbor)

17:00 Electron spin resonance spectroscopy using optically trapped polyatomic molecules

Optically trapped polyatomic molecules are a promising platform for measurements of time-reversal symmetry violation due to their highly polarizable structure, co-magnetometer states, and long achievable coherence times [Kozyryev and Hutzler, PRL 119 (2017)]. For example, linear polyatomic molecules in the vibrational bending mode could be used to search for the electron’s electric dipole moment (eEDM), which would cause the electron to precess in the effective electric field present in polarized molecules. Here we present microwave spectroscopy of the vibrational bending mode in optically trapped CaOH molecules, and discuss progress towards electron spin resonance spectroscopy with long coherence times. Applied to heavier molecules with otherwise identical structure, these measurements would have the potential to probe physics beyond the standard model approaching PeV energy scales.

17:00 Enhancing fiber atom interferometer by in-fiber laser cooling

Building cold atomic quantum sensors with photonic structures promise to miniaturize the apparatus that could eventually lead to portable devices. To prepare atoms in photonic platforms to a temperature that can be applied as a sensor requires adopting free-space laser cooling in space-constrained photonic structures. Here, we demonstrate in-fiber Λ-enhanced gray molasses and delta-kick cooling to cool atoms inside a 22-cm-long negative curvature hollow-core photonic crystal fiber from 32 μK to sub-μK in 4 ms. The in-fiber cooling overcomes the inevitable heating during the atom loading process and allows a shallow guiding optical potential to minimize decoherence. We employ these cold atoms in an inertia sensitive atom interferometer optically guided inside a hollow-core photonic crystal fiber with an interferometer time of 20 ms. The result improves the previous fiber guided atom interferometer sensitivity by three orders of magnitude. Our results permit bringing atoms close to source fields for sensing and could lead to compact inertial quantum sensors with a sub-millimeter resolution.
Reference: arXiv:2112.10088

17:00 Enriching the quantum toolbox of ultracold molecules with Rydberg atoms

Assembly of rovibrational ground-state NaCs molecules in an optical tweezer array will allow for high-fidelity quantum computation and the exploration of rich dipolar exchange Hamiltonians. Currently, these systems are limited by a minimum tweezer separation, which sets a hard cap on the interaction strength and increases the characteristic time for interesting physics. Further, readout requires re-separation into the component atoms, which is destructive and error-prone. We propose a hybrid array of optically-trapped molecules and atoms to solve these problems. By leveraging the large dipole moment of resonant Cesium Rydberg levels, we can increase the effective molecular coupling and achieve fast high-fidelity gates. The atoms can then be used as auxiliary qubits for entanglement and projective measurement, giving us a path towards nondestructive molecular readout. A near-term implementation of this scheme in our molecular qubit array can carry out 300ns entangling gates with potential gate and readout fidelities higher than 99.9%.

17:00 Experimental Quantum Control on IBM Quantum System

In resonance, pulse shapes have no effect on the population transfer; nevertheless, they affect the resonance response curves of the qubit. In this work, the experimental response curves of various pulse shapes were validated against the theoretical predictions. Furthermore, the effects of symmetrical cropping of the Lorentzian function at different heights were examined, using one of the open-access back-end IBM quantum processors.

17:00 Fabrication of atomic vapor cell for atomic sensors

We present detailed procedure and experimental setup to fabricate atomic vapor cell for atomic sensor application. A cell is 7.5 mm cubic with pyrex. The inner surfaces of the cell are coated with Aluminium Oxide. The cell is cleaned with distilled water, ethanol, and methanol respectively. The cell is baked in air at 550 degrees Celsius. The cell, then, is attached to high vacuum chamber with specially designed adapter. Rubidium atoms from the hot ampoule in vapor form are collected in a cold glass cell. Atfer that, we put 129Xe, 131Xe, nitrogen, and hydrogen gases into the cell for atom spin gyroscope. For atomic magnetometers, we put nitrogen into the cell.We will cover the performance of the atomic spin gyroscope and atomic magnetic field sensor using our cell in detail in the poster.

Speaker: Dr Sin Hyuk Yim (Agency for Defemse Development)

17:00 Functionalized Aromatic Molecules for Laser Cooling and Trapping

Laser cooling relies on photon cycling, which can be enabled in polyatomic molecules when an “optical cycling center” (OCC) is attached to an electronegative ligand. It was proposed that molecules with a (metal) alkaline-earth(I)-oxide-radical structure, would have good OCC properties and, thus, would be amenable to laser cooling [1]. More recent theoretical work has indicated that the alkaline-earth(I)-oxide unit attached to a benzene ring would offer a good OCC that would be tunable by substituting the ring hydrogen atoms with more electronegative species [2]. Theory has also indicated that larger rings (such as naphthalene, pyrene, and coronene) can also provide good optical cycling properties [3]. We report the results of dispersed fluorescence measurements on CaO-Ph-X (Ph : phenyl, X = F, CH3, CF3) in a cryogenic buffer gas at 9 K. We find that the vibrational branching ratio (VBR) to the ground vibrational state is ~95% for all species and 99% for CaO-Ph-3,4,5F [4]. We also study the napthol-based molecules CaO-Nap and SrO-Nap, and find that the 2-naphthyl positional variant of CaO-Nap also has a highly diagonal VBR, 96% [5]. These results demonstrate that the same principles that have led to laser cooling of di-, tri- and poly-atomic molecules (e.g. SrF, CaOH and CaOCH3) can likely be extended to phenolic and aromatic molecules.

[1] Kozyryev, et al, ChemPhysChem 2016, 17, 3641
[2] Dickerson, et al, PRL 2021, 126, 123002
[3] Dickerson, et al, JPCL 2021, 12, 3989–3995
[4] Zhu, et al, 2022, arXiv:2202.01881
[5] Mitra, et al, 2022, arXiv:2202.01685

17:00 High precision eigenvalues for the Rydberg S-states of helium for principal quantum numbers n > 10

In previous work, high precision eigenvalues for all states of
helium up to $n = 10$ and $L = 7$ have been obtained by the use of
double basis sets in Hylleraas coordinates [1]. In the present
work, we show that triple basis sets using three sets of
individually optimized nonlinear parameters for different distance
scales yield an order of magnitude improvement in accuracy for
basis sets of the same size for the Rydberg S-states states of
helium. They also allow an extension of high precision calculations
for the nonrelativistic energies and wave functions up to at least
$n = 16$ with little loss of accuracy. An important advance in
computational technique is the use of David Bailey's
double-quadruple (dq) precision arithmetic (approximately 70
decimal digits) in the optimization of the nonlinear parameters in
the basis set. Except for this, the wave functions have a high
degree of numerical stability, and standard quadruple precision is
sufficient for the evaluation of matrix elements. A comparison with
the best previous calculations for $n > 10$ [2] will be presented.

[1] G.W.F. Drake and Z.-C. Yan, Phys. Rev. A. 46, 2378 (1992).
[2] H. Nakashima and H. Nakatsuji, J. Chem. Phys. 128, 154108 (2008).

Speaker: Lamies Sati (University of Windsor)

17:00 High Speed THz Imaging with Rydberg Atoms

THz imaging and THz technologies are of great interest for a variety of applications, including non-destructive testing and medical diagnosis. Here, we demonstrate a THz imaging setup that employs Cs Rydberg atoms as THz-to-optical photon converters to provide full field images at many thousands of frames per second, that can be captured with conventional optical cameras.¹ The primary mechanism that enables this is the introduction of a strong visible decay pathway when the atoms are coupled with a terahertz field. Due to the density of Rydberg energy states, a relatively continuous spectrum of THz frequencies can imaged by careful choice of these states; we show imaging capabilities at 0.55THz and 1.05THz, for example. Full characterization of the system and progress towards a Rb imager will extend its versatility, and open up the potential for two-colour imaging.

[1] L. A. Downes, A. R. MacKellar, D. J. Whiting, C. Bourgenot, C. S. Adams, and K. J. Weatherill, “Full-field terahertz imaging at kilohertz frame rates using atomic vapor,” Phys. Rev. X 10, 011027 (2020).

17:00 Higher-order effects of electric quadrupole fields on a single Rydberg ion

Rydberg ions have large dipole and quadrupole polarizabilities which makes them extremely sensitive to external electric fields [1],[2]. As a result, an ion in the Rydberg state experiences altered trapping potential which leads to motion-dependent Rydberg excitation energies [3]. Higher the Rydberg state more is the sensitivity to the electric quadrupole trapping fields. The oscillating trapping field induces an energy shift in these states which oscillates at the trap drive frequency and generates sidebands in the spectrum. Unwanted couplings to these field-induced sidebands reduces the fidelity of Rydberg ion quantum gate operations. To mitigate this MW field are used which induces dressed states with opposite polarizabilities to create Rydberg state with vanishing polarizability which are insensitive to electric fields [4].

Here we study the higher order effects of the quadrupole electric filed on a single trapped Sr$^{+} $ Rydberg ion confined in a Paul trap, which arises due to the quadrupole polarizability of the Rydberg states. The effects were investigated on $ nS_{\frac{1}{2}} $and $ nP_{\frac{1}{2}} $ states and resonance shifts and spectral sidebands were observed experimentally. The Rydberg excitation energies depend quadratically on the trapping RF field amplitude. For the $ nS_{\frac{1}{2}} $ state the first order spectral sidebands were much weaker whereas in the $ nP_{\frac{1}{2}} $ state the spectrum showed a forest of sidebands. All results are in good agreement with theory [5].

References
[1] G. Higgins, A single trapped Rydberg ion. Phd. thesis, Stockholm University
and Innsbruck University, 2018.
[2] M. Muller, L. Liang, I. Lesanovsky, and P. Zoller, \Trapped Rydberg
ions: from spin chains to fast quantum gates," New Journal of Physics,
vol. 10, p. 093009, sep 2008.
[3] G. Higgins, F. Pokorny, C. Zhang, and M. Hennrich, \Highly Polarizable
Rydberg Ion in a Paul Trap," Physical Review Letters, vol. 123, 2019.
[4] F. Pokorny, C. Zhang, G. Higgins, and M. Hennrich, \Magic trapping
of a Rydberg ion with a diminished static polarizability," may 2020,
arXiv:2005.12422.
[5] G. Higgins, C. Zhang, F. Pokorny, H. Parke, E. Jansson, S. Salim,
and M. Hennrich, \Observation of second- and higher-order electric
quadrupole interactions with an atomic ion," Physical Review Research,
vol. 3, no. 3, pp. 1-6, 2021.

17:00 Imprinting persistent currents in fermionic superfluid rings

Persistent currents in a ring are one of the most striking manifestations of a quantum system coherence. The periodic boundary constrains the wavefunction phase to wind in a loop of an integer multiple of 2$\pi$, which, when non-zero, gives rise to a current. Besides being a proxy of quantum phase coherence, persistent currents represent a cornerstone for many applications, from precision sensing to quantum computing, that require a fast and controlled current injection and a reliable read-out of its magnitude. Here I present the experimental realization of a fast and on-demand generation of persistent currents in atomic Fermi superfluid rings and the investigation of the connection between their damping and vortex nucleation. We excite persistent current states of on-demand winding number by dynamically imprinting the phase winding in the ring with a tailored laser beam and we read-out the current state via an interferometric probe, which directly accesses the ring phase profile. We demonstrate our method to efficiently excite persistent currents of finite and controllable winding in the different interaction regimes of the BEC-BCS crossover. We then induce the current decay by inserting a small defect in the ring. For currents higher than a critical value, the obstacle triggers the emission of vortices that reduce the phase winding. Our work demonstrates fast and accurate control of persistent currents in fermionic superfluids, opening the route for their application in quantum technologies.

17:00 In-beam hyperfine spectroscopy of (anti-)hydrogen for tests of CPT and Lorentz invariance

Cold antihydrogen, the bound state of an antiproton and a positron, is an ideal laboratory to test the fundamental CPT symmetry, one of the cornerstones of the Standard Model of particle physics, by comparing its energy levels to ordinary hydrogen. Hydrogen is one of the best studied atoms experimentally, among the two best-known transitions is the ground-state hyperfine transition ν$_\mathrm{HF}$ with a relative precision of better than $10^{-12}$.

The ASACUSA collaboration has proposed a measurement of ν$_\mathrm{HF}$ in a beam, which allows to perform the experiment in a region far away from the strong magnetic fields needed for antihydrogen creation. Substantial progress has been made to improve the temperature and density of the positron plasma [1,2], which is expected to substantially increase the rate and ground-state fraction of antihydrogen atoms and thus for a measurement of ν$_\mathrm{HF}$. ASACUSA aims at an initial precision of 1 ppm, at which level the finite size of the antiproton becomes visible.

Initially with the aim to establish the in-beam method, ASACUSA has performed a measurement of ν$_\mathrm{HF}$ of ordinary hydrogen using a polarized beam and the same Rabi spectroscopy setup as will be used for antihydrogen and obtained a precision of 2.7 ppb [3]. Within the Standard Model Extension (SME) framework, that describes potential Lorentz invariance and CPT violation scenarios, also measurements using ordinary atoms can be used to constrain symmetry-violating SME coefficients [4]. First experiments have been performed on the orientation dependence of an external static magnetic field for hydrogen hyperfine measurements [5], and preparations are under way to study the hyperfine structure of deuterium.

References

[1] E.D. Hunter et al., EPJ Web of Conferences 262, 01007 (2022)
[2] C. Amsler et al., arXiv:2203.14890 [physics.plasma-ph]
[3] M. Diermaier et al., Nat Commun 8, 15749 (2017).
[4] V.A. Kostelecký & A.J. Vargas, Physical Review D 92, 056002 (2015).
[5] E. Widmann et al., Hyperfine Interact. 240, 5 (2019).

17:00 Investigating ultracold collisions with $^{23}$Na$^{39}$K ground-state molecules

Ultracold ground-state molecular quantum gases and mixtures yield highly complex and mostly unknown scattering behavior. In molecule-molecule collisions it ranges from the formation of long-lived four-body complexes to subsequent chemical reactions [1], photo-excitation [2] or spontaneous spin relaxation [3]. Atom-molecule collisions can give rise to tunable interactions such as Feshbach resonances [4] and might be used for evaporative cooling of molecules or trimer formation.
Here, we present our investigations of collisions with ultracold bosonic and chemical stable $^{23}$Na$^{39}$K ground-state molecules. In the pure molecular gas we probe photo-induced loss of four-body complexes in chopped optical dipole traps. We find the lower limit of the complex lifetime to be much larger than the lifetime derived from RRKM theory. In mixtures of $^{23}$Na$^{39}$K ground-state molecules with dense $^{39}$K atoms in different spin states, we find spin dependent loss rates. For one particular state of the $^{39}$K atoms, we observe unexpected suppression of the loss rate of several orders of magnitude below the universal scattering limit.
We also present our approach for the detection of such collisional events and product particles by state-selective ionization and VMI mass spectrometry [5] for our ultracold $^{23}$Na$^{39}$K ground-state molecules.
[1] Science, 2019, 366, 6469, 1111-1115
[2] Phys. Rev. Lett., 2020, 124, 163402
[3] arXiv, 2021, 2110.07501
[4] Science, 2019, 363, 6424, 261-264
[5] Phys. Chem. Chem. Phys., 2020, 22, 4861-4874

17:00 Investigation of laser frequency offset on nonlinear conversion in Lyman-alpha laser system

Generation of high power 121.6 nm light is vital for efficient laser cooling of antihydrogen. The nanosecond pulsed laser system developed for the ALPHA collaboration at CERN is presented here. It includes a high energy pulsed amplifier at 730 nm, followed by a doubling and subsequent gas phase third harmonic generation stage. We observe an anomalous frequency offset between the 730 nm seed laser input and the amplified light in the first stage. This leads to a frequency shift of the narrowband Lyman-alpha radiation and to a shift-dependent enhancement of the non-linear conversion process. Simulation of thermal-optical effects in the Ti:Sapphire amplifier crystals predict a similar frequency offset to experimental observation. Cavity alignment and off-resonant locking conditions introduce an additional frequency shift accompanied by an unprecedented increase in non-linear conversion to 121.6 nm radiation. The forthcoming paper will present supporting theoretical framework and simulation results of this phenomenon.

17:00 Large spin atoms in optical lattices : spin textures and correlations

Our experimental projects at the Laser Physics Institute (North Paris University) aim at characterizing entanglement for many-body systems made of large spin atoms. For this, we developed two experimental set-ups : one with large-spin strontium fermionic atoms, with spin-independent contact interactions; one with large-spin chromium bosonic atoms, with spin-dependent long-range dipole-dipole interactions.

I will describe our first measurements of the spin distribution of the SU(N) Fermi gas made of strontium atoms. For this, we used a spin-orbit coupling scheme, where a retroreflected laser beam selectively diffracts two spin components in opposite directions. Spin sensitivity is provided by sweeping through a magnetic-field sensitive transition while dark states ensure that spontaneous emission remains low.

On the chromium machine, we investigated the spin dynamics and quantum thermalization of a macroscopic ensemble of S = 3 spins initially prepared in a pure coherent spin state. The experiment uses a unit-filled array of 10 thousand chromium atoms in a three dimensional optical lattice. Atoms interact at long distance under the effect of magnetic dipole-dipole interactions, realizing the spin-3 XXZ Heisenberg model with long-range couplings. We investigated the build-up of quantum correlations in this many-body system. For this, we measured collective properties such as the total population in the seven different Zeeman states, or the collective spin length. We also found that the measurement of magnetization fluctuations provides direct quantitative estimates for two-body correlations.

References: Youssef Aziz Alaoui et al., arXiv:2201.07277 (to be published in Phys. Rev. Lett.)
Lucas Gabardos et al., Phys. Rev. Lett. 125, 143401 (2020)
P. Bataille et al., Phys. Rev. A 102, 013317 (2020)

17:00 Low uncertainty absolute frequency measurement of the strontium ion optical clock transition

The electric quadrupole transition of the $^{88}$Sr$^+$ ion at 445 THz is one of 11 recommended optical transitions that can be used as secondary representations of the SI second. Progress towards the redefinition of the SI second using an optical clock indicates that a new definition will be based on either one atomic optical transition or an ensemble of such reference transitions, selected from the recommended frequencies. One criteria that must be met before the SI second is redefined is continuity with the current definition of the SI second as realized with cesium fountain clocks, at a level of $3\times10^{-16}$ or better.

Here, we report a new absolute frequency measurement of the $^{88}$Sr$^+$ ion optical transition. The measurement campaign of the ion frequency lasted 12 days in June 2017, and provided 92 hours of comparison data with a local maser flywheel oscillator at NRC. The link between the optical standard and the SI second was completed by measuring the maser continuously during the month of June 2017 with respect to the SI second using a GPS link. The SI second is realized with primary
and secondary frequency standards (PSFS) that report to the BIPM. The maser frequency (UTC(NRC)), averaged over a 30-day period, is provided in the Circular T #354 report published by the BIPM.

The uncertainty of the absolute frequency measurement has three dominant components of comparable values ($2.2$ to $2.5 \times 10^{-16}$): the dead time uncertainty caused by the intermittent operation of the optical clock, the GPS link uncertainty, and the uncertainty of the realization of the SI second with the PSFS. The optical clock evaluated uncertainty of $1.2\times10^{-17}$ is insignificant in comparison. The main improvements compared to previous measurement campaigns are a better evaluation of the dead time uncertainty based on a noise model of maser, and the use of a maser with better noise characteristics than previously available.

The frequency measurement accuracy has a fractional uncertainty of $4.2\times10^{-16}$. This is a factor of four better than our our previous best determination and represents a significant step towards meeting the continuity criterion with the current definition of the SI second.

17:00 Magnetically mediated hole pairing in fermionic ladders of ultracold atoms

The Fermi-Hubbard model is an iconic model of solid state physics that is believed to capture the intricate physics of strongly correlated phases of matter such as High-Tc superconductivity. Such a state of matter is supposedly achieved upon doping a cold antiferromagnetic Mott insulator. Pairing of dopants (holes), in particular, is considered to be a key mechanism for the occurrence of unconventional superconductivity.

Here, I will present our experimental observation of hole pairing due to magnetic correlations in a Fermi-Hubbard-type system in our Lithium quantum-gas microscope. We engineer mixed-dimensional Fermi-Hubbard two-leg ladders in which a potential offset between the legs suppresses the tunneling along the rungs, while enhancing spin exchange and singlet formation, thus drastically increasing the hole binding energy. We observe in particular that holes preferably sit on the same rung in order to maintain magnetic ordering, and we extract a binding energy on the order of the spin exchange energy. We furthermore find indications for repulsion between pairs when there are several hole pairs in the system.

Speaker: Thomas Chalopin (Max-Planck-Institute for Quantum Optics)

17:00 Mesoscopic transport with a weakly-interacting Bose gas

Ultracold atomic gases play crucial roles in revealing nontrivial quantum transport phenomena. Especially, quantum transport of weakly-interacting Bose gases would be interesting in that the realizations with condensed-matter systems are difficult. In this poster, I focus on two-terminal transport systems with Bose-Einstein condensates. In spite of the formal similarity with fermionic superconducting systems, it is shown that the current-bias characteristics in Bose-Einstein condensates is quite different due to the presence of a unique transport process existing in the condensates.

17:00 Micro-integrated laser and frequency reference modules for operation in quantum technology applications

The Ferdinand-Braun-Institute has been developing micro-integrated, high-power, narrow-linewidth semiconductor laser sources for precision spectroscopy applications for more than ten years. Starting with hybrid-integrated diode laser chips and micro-optics on a ceramic platform, we successfully enabled Bose-Einstein condensation experiments in a drop tower [1][2]. As the next step we now develop, qualify, and deliver whole laser modules for applications on space-borne platforms including sounding rockets, the International Space Station and small satellites [3]. Here, we present two novel devices for operation in quantum technology applications: A hybrid micro-integrated laser module and a frequency reference module.

A robust design will enable the deployment of our latest micro-integrated diode laser modules in space applications. Specially developed control algorithms shall ensure enhanced functionality and user-friendliness. Temperature stabilization is achieved by the calculation of an effective micro-optical bench temperature through distributed temperature sensors. By that the optical resonator length and hence the optical emission frequency is stabilized. An intra-cavity pick-off will enable the generation of an error signal allowing to extend the laser’s mode-hop free tuning range beyond the limit given by the free spectral range of the laser resonator.

Especially tailored to meet the requirements of laser automation in quantum technology applications, a compact and robust frequency reference module is being developed. By an intermediary stabilization of the laser to the well-designed frequency reference, laser locking to a desired atomic transition is accelerated. A sophisticated thermal stabilization concept shall ensure a frequency accuracy of 50 MHz and a tuning range of more than 20 GHz. The reference module is designed to be operated in three different modes: (i) Stabilization of a laser to the frequency reference for achieving an accelerated lock-acquisition, (ii) Operation of the frequency reference as a wavemeter and measuring the emission frequency of a free-running laser and (iii) recalibration of the frequency reference with a reference laser. In its first application the frequency reference is intended to complement the laser module by facilitating accurate control of the laser frequency in an atom interferometer application with ultra-cold potassium atoms.

References

[1] Max Schiemangk et al., Appl. Opt. 54, 5332-5338 (2015)
[2] Julia Pahl et al., Appl. Opt. 58, 5456-5464 (2019)
[3] Christian Kürbis et al., Appl. Opt. 59, 253-262 (2020)

17:00 Multimode microwave-to-optical conversion in warm 87-Rb atoms

The ability to convert quantum signals between the microwave and optical domains is an important tool in quantum information processing. Here, we use a room-temperature ensemble of $^{87}{\rm Rb}$ atoms inside a microwave cavity to generate an optical signal whose frequency is the sum of an optical pump and a hyperfine microwave control field, using hybrid sum-frequency generation [1]. By using a multimode microwave control field, the generated optical field carries the same multiple-frequency character, which can be as broad as the 300-kHz cavity linewidth and tunable across the 0.5-GHz Doppler spectrum. This process, which leverages electromagnetically-induced transparency between the two optical fields, results in a “slow-light” time delay of the converted field, where the delay time depends on the power of the microwave control field [2].

Using these techniques, our gaseous atomic system acts in analogy to an electro-optic modulator, which, with its capacity to operate under ultra-low pumping powers, makes it a promising platform for quantum frequency processing [3] across several orders of magnitude in the frequency domain.

Figure 1. (a) In the nonlinear sum-frequency generation process, microwave frequency $\omega_\mu$ and optical frequency $\omega_c$ combine to produce an optical frequency at $\omega_p = \omega_\mu + \omega_c$. (b) Diagram of the experimental setup. Microwave signal generator (SG), spectrum analyzer (SA), acousto-optic modulator (AOM), external cavity diode laser (EDCL), photodiode (PD), quarter waveplate (QWP), amplifier (AMP).

---

[1] K. V. Adwaith, A. Karigowda, C. Manwatkar, F. Bretenaker, and A. Narayanan. "Coherent microwave-to-optical conversion by three-wave mixing in a room temperature atomic system." Opt. Lett. 44 1 (2019).

[2] J. K. Saaswath, K. N. Pradosh, K. V. Adwaith, B. C. Sanders, F. Bretenaker, and A. Narayanan. "Microwave-driven generation and group delay control of optical pulses from an ultra-dilute atomic ensemble." Opt. Express 29 11 (2021).

[3] H.-H. Lu, J. M. Lukens, N. A. Peters, O. D. Odele, D. E. Leaird, A. M. Weiner, and P. Lougovski. "Electro-optic frequency beam splitters and tritters for high-fidelity photonic quantum information processing." Phys. Rev. Lett. 120 030502 (2018).

17:00 Nanostructured Alkali-Metal Vapor Cells

We have developed a methodology for manufacturing alkali-metal vapour cells with internal confinement dimensions down to hundreds of nanometers (generally less than the probe laser wavelength). We envisage our nano-cells as a platform for fundamental atom-light interaction experiments, as well as for potential technological applications. Our manufacture process is versatile and our fused-silica cells are robust. The figure below, from our recent paper [Cutler et al, Phys. Rev. Applied 14, 034054 (2020)], shows a schematic and photograph of one of our nano-cells, as well as some example etched nano-structures. Similar cells have already been used to investigate the cooperative Lamb shift in a dense atomic vapour, measure the atom-surface van der Waals interaction, and to study the spectral response and transit time broadening of the vapour under evanescent excitation. This poster will describe recent experiments and developments using our nano-cell platform.

Speaker: Tom Cutler (Durham University)

17:00 Narrowband biphoton source of maximal spectral brightness at ultralow pump power

Nonclassical photon sources of high brightness are key components of quantum communication technologies. We here demonstrate the generation of narrowband, nonclassical photon pairs up to the ultimate limit of achievable generated spectral brightness at which successive photon pairs start to overlap in time.

Our biphoton source employs spontaneous four-wave mixing in an optically-dense ensemble of cold Rubidium atoms within a hollow-core fiber. To avoid collisions of the cold atoms with the fiber wall, thereby reducing the coherence time, the atoms are guided by an optical dipole trap. By using cold atoms we achieve an orders of magnitude lower biphoton bandwidth as compared to fibers filled with warm gases. As an additional benefit of the hollow-core fiber, all light fields involved in the FWM process are guided in the same optical mode. Thus, we obtain intrinsically optimal mode-matching as well as strong light-atom coupling at orders of magnitude lower pump powers compared to free space experiments. This results in a generated spectral brightness per pump power of up to $2\times10^9 \ \mathrm{pairs}/(\mathrm{s}\cdot\mathrm{MHz}\cdot\mathrm{mW})$, which is a 10-fold increase over the previous record. Additionally, our results are achieved at a 100-fold reduced pump power and exhibit a 10-fold lower bandwidth of $2\pi \times 6.5\ \mathrm{MHz}$, which is directly compatible with atomic quantum memories. We verify the nonclassical character of the generated photons with a 97-fold violation of the Cauchy-Schwarz inequality. We further demonstrate that our source can be used as a heralded single-photon source with a heralded auto-correlation as low as $0.08$. Moreover, we show that our biphoton source can be tuned to the ultimate achievable limit of generated spectral brightness, at which successive photon pairs start to overlap in time. In this regime, the photon correlations clearly start to deviate from the expected behavior for low brightness sources.

As the photon pairs at wavelengths of $780/795 \ \mathrm{nm}$ exhibit orthogonal polarizations and are emitted into a single spatial mode, they can be efficiently separated and interfaced to photonic networks as well as atomic quantum memories. Our source combines the advantages of atomic ensembles and waveguide environments, thus representing a step towards interfacing ensemble-based building blocks with photonic quantum networks.

17:00 Nonequilbrium states of driven-dissipative quantum gases

A system of ultracold atoms can be brought in contact with a thermal bath by letting it interact weakly with a large cloud of another atomic species. We consider atoms in a time-periodically driven optical lattice in contact with an interacting Bose condensate and microscopically model them using Floquet-Born-Markov theory. The interplay of driving and dissipation will guide these systems into non-equilibrium steady states. Compared to the usual adiabatic state preparation, suffering from non-adiabatic excitation processes, this scenario can have two advantages; it is robust, since energy (and entropy) can be dumped into the bath, and it allows for the preparation of interesting states beyond the strict constraints of thermal equilibrium. I will present two examples in rather different regimes: (i) In a system of fermions loaded into the Floquet-topological band structure of a hexagonal lattice created by high-frequency driving, the coupling to the environment allows to “cool” almost all particles into a single band so that a topological insulator giving rise to a quantized Hall response is prepared [1]. (ii) Subjecting a one-dimensional bosonic system to a spatially local drive of intermediate frequency that resonantly excites (heats) the system, the interplay of driving and dissipation is found to give rise to the formation of a non-equilibrium Bose condensate in a subspace that approximately decouples from the drive [2]. Finally, I will also address the (experimental and numerical) observation of a dynamical phase transition occurring at a critical time during the bath-induced relaxation dynamics of an open system [3].

[1] A. Schnell and A. Eckardt.: Stabilizing a Floquet topological insulator in a driven optical lattice by bath engineering (in preparation).
[2] A. Schnell, L.-N. Wu, A. Widera, A. Eckardt.: Floquet-heating-induced non-equilibrium Bose condensation in an open optical lattice (preprint, arXiv:2204.07147).
[3] L.-N. Wu, J. Nettersheim, J. Feß, A. Schnell, S. Burgardt, S. Hiebel, D. Adam, A.E., A. Widera, A. Eckardt: Dynamical phase transition in an open quantum system (in preparation).

17:00 Observation of Stochastic Wavefunction Evolution from Dispersively Measured Bose-Einstein Condensates

A fundamental tenet of quantum mechanics is that measurements change a system's wavefunction to that most consistent with the measurement outcome, even if no observer is present. Weak measurements produce only limited information about the system, and as a result only minimally change the system state. In this context, the interaction of a nearly closed quantum system with its environment can be described as a continuous weak measurement process. Bose-Einstein condensates (BECs) offer multiple weak measurement techniques, that yield a controlled reservoir and consequently allow time-resolved study of the system evolution. We theoretically and experimentally characterize the quantum projection noise in atomic BECs weakly measured by the light scattered from a far-from resonant, i.e., dispersivly interacting, laser beam. We quantify the resulting wavefunction change with two observations: the contrast in a Ramsey interferometer, and the deposited energy. Next, we present a versatile high-resolution ultracold atom microscope: a combined hardware/software system that recovers near-diffraction limited performance and minimizes the information loss. Our high-fidelity digital correction technique reduces the contribution of photon shot noise to density-density correlation measurements, which would otherwise contaminate the quantum projection noise signal in weak measurements [1]. We demonstrate our aberration compensation technique using phase contrast imaging, a dispersive homodyne detection technique directly applicable to quantum back-action limited measurements.
[1] E. Altuntas, and I. B. Spielman, Physical Review Research, 3, 043087 (2021).

17:00 Observation of two-photon induced fluorescence of neutral carbon atom gases

Ultracold atoms, made possible by laser cooling and trapping, are used as platforms for a wide range of applications such as observation of quantum degeneracy [1], quantum simulation [2], frequency standards [3] and ultracold collision studies [4]. While experiments using ultracold atoms of alkali metals and alkaline earth metals have made great progress, laser cooling has not been realized for atomic species of chemical and biological interest including carbon and hydrogen. The reason is that the optically allowed electronic transitions from the ground state of these atoms lie in the vacuum ultraviolet (VUV) region, making it difficult to construct light sources to drive effective cooling. In the case of carbon, laser cooling on two-photon transitions with a mode-locked laser has been discussed [5]. However, a gas production method in vacuum for neutral carbon with low vapor pressure has not been established. Furthermore, to the best of our knowledge, two-photon excitation of carbon atoms in vacuum has not also been demonstrated.
Here we demonstrate gas production of carbon atoms in the ground state using laser ablation of a graphite in vacuum and observation of produced atoms through two-photon induced fluorescence. This method is expected to be a fundamental technique applicable to laser cooling of carbon.
Figure 1 shows the experimental setup and the schematic energy level diagram of carbon showing the involved levels and transitions. Carbon atoms were produced by focusing the 266 nm radiation from the fourth harmonic of a Q-switched Nd:YAG laser on a rotating highly oriented pyrolytic graphite (HOPG) target. Produced particles including ions and molecules as well as atoms were expanded in a vacuum chamber.

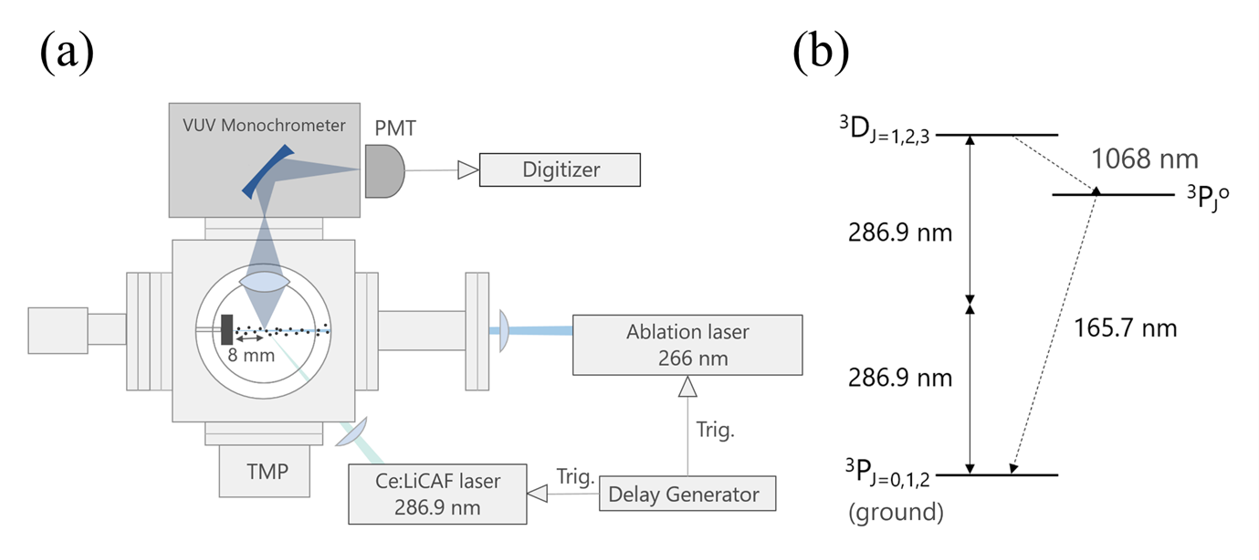
Nanosecond pulses from a homebuilt, tunable Ce:LiCAF laser pumped by the fourth harmonic of another Q-switched Nd:YAG laser were used for the two-photon excitation. The laser wavelength was tuned to the two-photon resonances of the $^{3}$P-$^{3}$D transition at 286.9 nm. The laser beam was focused into a spatial region at a distance of 8 mm from the target. The delay time between atomic gas production and two-photon excitation was adjusted with a digital delay generator. The two-photon induced fluorescence at 165.7 nm was detected perpendicular to both the excitation laser beam and the atomic beam. A 0.2 m monochromator equipped with a solar-blind photomultiplier tube (PMT) was used for the detection.
We will introduce the density and the temperature of produced atoms evaluated through the observation of the two-photon induced fluorescence. It was confirmed that when the laser fluence was excessively high, carbon atoms were produced in the high-energy excited states with long lifetimes unsuitable for laser cooling. The dependence of the behavior of the produced particles on the laser fluence will be discussed in conjunction with the results of plume emission spectra and time-resolved emission measurements. In addition, the precooling method for actual laser cooling of the atoms produced by our method and the design of our cooling laser at a wavelength of 286.9 nm will also be presented.
This work is supported by JST Precursory Research for Embryonic Science and Technology Grant Number JPMJPR190B and MEXT Quantum Leap Flagship Program Grant Number JPMXS0118067246.
[1] M. H. Anderson et al. Science 269, 198 (1995).
[2] M. Greiner et al. Nature 415, 39 (2002).
[3] H. Katori et al. Phys. Rev. Lett. 91, 173005 (2003).
[4] S. Inouye et al. Nature 392, 151 (1998).
[5] D. Kielpinski. Phys. Rev. A 73, 063407 (2006).

17:00 Precision calculation of polarizability of heavy ions and atoms for physisorption with 2D materials

The calculations of different properties of the atoms and ions play a crucial role in many applications of various fields for instance, atomic physics, material science, astronomy, plasma, nanotechnology etc. An accurate description of different atomic properties is highly challenging with the standard approximations resulting in failure in providing the good data. Therefore, the surge for accurate calculation of atomic properties has emerged from last decade using promising theoretical methods. Here, in this paper, we have evaluated one of the most important atomic property i.e., dipole polarizability of heavy ions - Zn$^+$, Cd$^+$, Hg$^+$, Pb$^+$ and atoms – Zn, Cd, Hg and Pb using two different relativistic many body methods. The known dynamic dipole polarizability values at imaginary frequencies are then used to derive characteristic van der Waal (vdW) dispersion coefficients with two dimensional (2D) materials - graphene and carbon nanotube walls, essential for physisorption applications. The agreement of the calculated dispersion coefficients is satisfactory with the recent study conducted using density functional theory (DFT) for the case of graphene. The present work is useful in sensing and storage applications of heavy elements with the considered 2D material walls. The future aspect of this work includes the accurate modelling of vdW correction based on inclusion of the higher-order coefficients which can be used to procure a higher accuracy towards total vdW potential between element and material wall.

Speaker: Ms Harpreet Kaur (Guru Nanak Dev University)

17:00 Progress on the CeNTREX TlF Schiff Moment Search

The The aim of CeNTREX (Cold molecule Nuclear Time-Reversal Experiment) is to search for the proton’s electric dipole moment by measuring the Schiff moment it induces in the $^{205}$Tl nucleus. We use the amplified energy shift from the Schiff moment that is present in the polar molecule thallium fluoride (TlF). To maximize the population of the science state, we employ rotational cooling on the cold TlF beam, which pumps lowest few rotational states into a single J=0 hyperfine level of the $^1$Σ$^+$ electronic ground state. Electrostatic focusing with a quadrupole lens will be used to efficiently direct molecules to a downstream detection region; this requires a weak-field seeking state. This is achieved by adiabatic state transfer from J=0 to J=2 with microwaves. Finally, the Schiff moment measurement requires careful nulling of magnetic fields in the interaction region. Characterization of a new magnetic shielding system is ongoing.

*This work is funded by the Heising-Simons Foundation, NSF and the U.S. DOE, Office of Science, Office of Nuclear Physics, under contract DE-AC02-06CH11357.

17:00 Progress on Zeeman slowing of CaF

Recently, great progress has been made in direct laser cooling of molecules to temperatures close to absolute zero. However, experiments are limited by the number of molecules that can be captured from molecular beams using typical laser-based trapping methods. In Petzold et al. 2018, we proposed to transfer Zeeman deceleration to laser-coolable molecules and thus substantially increase the number of molecules that can be captured by e.g. magneto-optical traps. Here, we now present our characterisation of the Zeeman force for CaF molecules. We find excellent agreement of the force with an optical Bloch equation model. This shows that the generated force profile can compress the initial molecular velocity distribution from a standard buffer gas cell to the velocity required for trapping in a magneto-optical trap (MOT). We present the current status of our experiment as well as theoretical work on a novel Bayesian-optimised molecular MOT scheme for CaF molecules.

17:00 Progress Towards Measuring the Nuclear Magnetic Quadrupole Moment in YbOH Molecules

Measurements of heavy, polar molecules in the gas-phase are sensitive experimental probes of Parity (P) and Time reversal (T) violating new physics. The large internal fields and relativistic electron dynamics in these molecules amplify potential sources of P,T violating physics, such as the electron’s electric dipole moment (eEDM) or a nuclear magnetic quadrupole moment (NMQM). Molecular beam measurements of an NMQM would provide a modern probe of P,T violating physics in the hadronic sector, complimentary to existing eEDM constraints on new leptonic physics. We present progress toward measuring the NMQM on the $^{173}$Yb nucleus in a beam of cold $^{173}$YbOH molecules. The polyatomic structure of YbOH enables full control of polarization in the vibrational bending mode, while retaining the ability to cycle photons and laser-cool. Our progress on YbOH includes: preliminary spin precession in the vibrational ground state, spectroscopy of the vibrational bending mode, demonstration of cycling in the odd isotopologues, and construction of a magnetically shielded science chamber for precision measurement.
We acknowledge support from NIST, NSF, the Heising-Simons Foundation, the Gordon and Betty Moore Foundation, and the Alfred P. Sloan Foundation. Y.T. acknowledges support from the Masason Foundation. P.Y. acknowledges support from the Eddleman Fellowship.

17:00 Quantum Correction to Josephson Oscillations

We theoretically investigate a bosonic Josephson junction by using the path-integral formalism with relative phase and population imbalance as dynamical variables. Starting from a Lagrangian of a Bose Josephson junction, we derive an action only in terms of relative phase by performing functional integration over the population imbalance. We then analyze the quantum only-phase action, which formally contains all of the quantum corrections. To the second order in the derivative expansion and to the lowest order in $\hbar$, we finally obtain the quantum correction to the Josephson frequency of oscillation in the Josephson regime [1]. The identical quantum correction is found also by adopting an alternative approach. While the estimated quantum correction to the Josephson frequency is relatively small based on current experimental setups, we expect that the correction can be significant by appropriately tuning some parameters such as the onsite interaction strength in an atomic Josephson junction or the capacitance in a superconducting Josephson circuit. Our predictions would be a useful theoretical tool for experiments with atomic or superconducting Josephson junctions.

[1] K. Furutani, J. Tempere, and L. Salasnich, Phys. Rev. B 105, 134510 (2022).

17:00 Quantum science with programmable Strontium arrays in a Hubbard lattice

Alkaline earth atoms and optical tweezer arrays are naturally complementary technologies. The atoms provide convenient transitions for high fidelity optical cooling and imaging, well-controlled internal states with extremely high quality factors, and switchable interactions. The tweezers further provide programmable control over those atoms' motional states and positions. These capabilities make this an attractive platform for studying quantum optics, with the ability to programmably prepare and detect Fock states of many indistinguishable, non-interacting bosons, and to study how those boson propagate through reconfigurable linear optical networks implemented with optical tweezers and an optical lattice. Conversely, this platform can also be used to study strongly interacting systems - namely collections of optical clock qubits that can be entangled via Rydberg interactions to study problems in quantum sensing, and simulations of spin models. The combination of universal control over optical clock qubits, coherent itinerance, and tunable interactions could ultimately be combined to study a large class of condensed matter Hubbard models.

Speaker: Aaron Young (JILA)

ICAP_2022_AY.png

17:00 Quantum sensor networks as exotic field telescopes for multi-messenger astronomy

Multi-messenger astronomy, the coordinated observation of different classes of signals originating from the same astrophysical event, provides a wealth of information about astrophysical processes. So far, multi-messenger astronomy has correlated signals from known fundamental forces and standard model particles like electromagnetic radiation, neutrinos and gravitational waves (GW). Many of the open questions of modern physics suggest the existence of exotic fields with light quanta (masses $\ll {\rm 1~eV/c^2}$). Quantum sensor networks could be used to search for astrophysical signals predicted by beyond-standard-model theories which address these questions. Here, we show that networks of precision quantum sensors that by design are shielded from or are insensitive to conventional standard-model physics signals can be a powerful tool for multi-messenger astronomy. We consider the case where high-energy astrophysical events produce intense bursts of exotic low-mass fields (ELFs), and we propose a novel model for the potential detection of an ELF signal based on general assumptions. We estimate ELF signal amplitudes, delays, rates, and distances of GW sources to which global networks of atomic magnetometers and atomic clocks could be sensitive. We find that such precision quantum sensor networks can function as ELF telescopes to detect signals from sources generating ELF bursts of sufficient intensity.

Details in Nature Astronomy 5, 150 (2021)

17:00 Realization of a ferromagnet in an atomic superfluid

Interactions in materials characterized by spin degrees of freedom play a crucial role in determining the magnetic properties both in the presence and in the absence of an external coherent drive. For instance, if the spin-dependent interaction is positive and strong as compared to the external drive the material behaves as a ferromagnet, otherwise it shows a paramagnetic response to external perturbations.

By means of accurate control of the spin degrees [1,2], and of polarization-resolved spatial imaging in a coherently-driven 23Na Bose-Einstein condensate we explore the magnetic phase diagram of an extended superfluid. In the limit of strong external driving or small spin-dependent interaction (low density) the system features a paramagnetic response whereby the polarization is determined by the frequency detuning of the drive, while in the opposite limit of strong spin interaction the systems shows typical ferromagnetic behaviour with hysteresis, formation of magnetic domain walls, and divergent magnetic susceptibility.

Using a similar experimental setup we perform complementary measurements of the spin dispersion relation of a two-component superfluid demonstrating the massive (gapped) character of collective excitations when the superfluid is subject to stationary resonant driving [3], and of the role of quantum torque under strongly nonstationary driving [4].

[1] A. Farolfi et al., Rev. Sci. Instrum. 90, 115114 (2019).
[2] A. Farolfi et al., Phys. Rev. A 104, 023326 (2021).
[3] R. Cominotti et al., Phys. Rev. Lett. 128, 210401 (2022).
[4] A. Farolfi et al., Nat. Phys. 17, 1359 (2021).

17:00 Relativistic corrections to two-photon decay rates in heliumlike ions

Two-photon transition rates are important in determining astrophysical quantities such as population balance in planetary nebulae. Our group recently calculated two-photon decay rates in heliumlike ions including the finite nuclear mass effects [1]. We have now perturbatively added relativistic corrections to these results, giving the most precise and accurate calculations to date for these transitions. In the process of calculating the two-electron Breit matrix elements, we first tested the derived two-photon, two-electron decay (2nd order field +1st order relativistic) perturbation equation on the equivalent one-electron process which obeys the same formula. In this process, we derived (and will report on) one-electron Breit-Pauli operators that were shown to be equivalent to the corresponding Dirac operators. A continuous gauge parameter is considered, and the operators are compared to the long-wavelength QED operators derived for few-electron atoms by Pachucki [2].

[1] Bondy, Aaron T., Donald C. Morton, and G. W. F. Drake. "Two-photon decay rates in heliumlike ions: Finite-nuclear-mass effects." Physical Review A 102.5 (2020): 052807
[2] Pachucki, Krzysztof. "Long-wavelength quantum electrodynamics." Physical Review A 69.5 (2004): 052502.

Funding from NSERC and QE-II is gratefully acknowledged.

17:00 Rotation Sensing Using Point Source Atom Interferometry

In Point Source Atom Interferometry (PSI), a sequence of Raman laser pulses interact with an expanding ball of cold atoms, to split, redirect and recombine the matter-wave. It exploits the correlation between the position and velocity of the atoms to produce a spatially imprinted interference pattern across the atomic cloud. Since the phase of atoms contains information about inertial effects on the system, the interferometer can be used to detect angular rates. PSI can therefore be used as a sensor that can take measurements for inertial navigation applications. We plan to develop such a rotation sensor and test out optimal control pulses to improve the performance of the interferometer, tackling issues involving scale factor instability and low contrast. As a preliminary step, we characterised the response of the I&Q modulator needed to control the phase of the optimal pulses, thus reducing the errors caused by potential non-linearities.

17:00 Rydberg Engineering: Recent Techniques for Sensitive Field Measurements

Highly-excited Rydberg atoms have been used for International System of Unit (SI)-traceable radio-frequency (RF) electric field and power measurements, but are limited in sensitivity to order 100 $\mu$V/m/$\sqrt{Hz}$ by noise and linewidth issues. These Rydberg atom-based sensors have far-reaching capabilities, ranging from SI-traceable measurements to receiving communication signals, even streaming video. We survey several recent experimental schemes and analysis techniques which help increase sensitivity in Rydberg spectroscopy measurements. Two methods to amplify signals without introducing electronic noise are the optical homodyne detection scheme to reduce laser power noise fluctuations, and using a metamaterial split-ring resonator to enhance the field at the location of the atoms. Linewidths can be narrowed via significant experimental adjustments, such as cooling atoms or using Doppler-narrowed three-photon schemes, which are efficiently simulated via a new calculation method. We also examine methods to lower the noise floor of the 'super-heterodyne’ scheme, which enables detection of phase and amplitude for very weak RF signals using an RF local oscillator, as well as a separate 'all-optical’ phase detection method in Rubidium. We also develop theoretical methods for fitting experimental spectra which are broadened by spatially inhomogeneous fields, as are present in vapor cells and unmatched waveguides. Each of these methods helps increase sensitivity of atomic electric field measurements, to the point where they have enabled wireless live video reception. Taken together, they demonstrate the many opportunities in Rydberg engineering for refining measurements.

17:00 Self-pinning transition in a mixture of two non-identical Luttinger Liquids

The pinning quantum phase transition can be observed in both weakly interacting quantum many-body systems described by a 1D Bose-Hubbard model and strongly interacting 1D systems modelled by Luttinger liquid theory. In both these cases an ultra-cold quantum gas can be driven to Mott-insulating state by imposing an infinitesimal small external lattice potential [1]

Recently an analogue to this transition was found for a Tonks-Girardeau gas that is immersed in a Bose-Einstein condensate, which corresponds to a situation of self-pinning state without imposing any external lattice potential [2].

Based on these studies, I present our work on this phase transition by studying a mixture two non-identical Luttinger liquids, whose physical properties can be adjusted from being weakly to strongly correlated. In addition the system allows one to tune the interaction between the components, which therefore gives access to the full phase diagram of the two-component gas. While we are particularly interested in the behaviour of the phase transition as a function of correlations, I will also point out the implications for these systems to act as phonon-carrying matter wave lattices.

References
[1] E. Haller, R. Hart, M. J. Mark, J. G. Danzl, L. Reichsöllner, M. Gustavsson, M. Dalmonte, G. Pupillo, and H.-C. Nägerl, Pinning quantum phase transition for a Luttinger liquid of strongly interacting bosons, Nature (London) 466, 597 (2010)
[2] T. Keller, T. Fogarty and T. Busch, Self-Pinning Transition of a Tonks-Girardeau Gas in a Bose-Einstein Condensate, Phys. Rev. Lett., 128, 053401 (2022)

17:00 Silicon-photomultiplier embedded photodetector for ACME III

A measurement of the electron electric dipole moment (eEDM) is a powerful probe for the existence of physics beyond the Standard Model of particle physics. The ACME experiment searched for eEDM with the world's highest sensitivity using cold ThO polar molecules (Nature, 562 (2018) 355-360). One of the improvements for the next generation of the ACME experiment is using silicon photomultipliers (SiPMs) as LIF photon detectors instead of PMTs. We have developed a dedicated SiPM module and evaluated its performance. The SiPM module shows about a 2.5 times higher detection efficiency than the PMTs used in the previous ACME experiment. This reports the design and results of performance test of the SiPM module.
This work was supported by the National Science Foundation, the Gordon and Betty Moore Foundation, the Alfred P. Sloan Foundation, JSPS KAKENHI, and Okayama University RECTOR program.

17:00 Site-Resolved Imaging of a bosonic Mott insulator of 7Li atoms

In this poster, we report a quantum gas microscope of Lithium-7 atoms in a two-dimensional (2D) square lattice. Individual atoms in each lattice site are imaged by Raman sideband cooling in a hybrid potential of the 2D lattice and a single tightly focused optical sheet potential. With a high numerical aperture (NA=0.65) objective, we achieve a point spread function of 630nm (full width half maximum), which is small enough to resolve the lattice spacing (752nm). About 4000 photons were collected during 1s of exposure time with a detection fidelity of 98%. Using the magnetic Feshbach resonance, we produce a large-sized unity filling Mott insulator with 1500 atoms at low temperature. We engineer our potential on a single-site level with an optical potential generated by a digital micromirror device (DMD), which opens opportunities to further cool the temperature and explore many-body localized (MBL) phases.

17:00 Site-resolved rotational state control of an optical tweezer array of ultracold dipolar molecules

Ultracold polar molecules are able to interact at long-range via electric dipole-dipole interactions, which can be used to generate entanglement between distant molecules by coherently coupling their rotational quantum states. This capability makes such molecules an attractive platform for simulation of quantum matter and for quantum computing. We present our recent work on coherent control of the rotational and hyperfine degrees of freedom of a 1D array of ultracold NaCs molecules in optical tweezers. We perform coherent microwave spectroscopy of the molecules in the rotational ground and first excited state manifold. We further demonstrate site-selective excitation of individual molecules using a global microwave pulse by varying the light-shift induced by the tweezer beams at different sites, which allows us to arbitrarily position rotational excitations in our molecule array. Finally, we present our progress towards engineering coherent transfer of rotational excitations between sites via dipole-dipole coupling.

17:00 Striped Self-Bound Dipolar Droplets

We investigate a system of dipolar atoms confined to move on a two dimensional plane. The dipole moments are all parallel and aligned in a direction that does not
necessarily coincide with the normal to the plane. As a result of the attractive and repulsive components of the dipole-dipole interaction, the system can form a self-bound system, which is stabilized by quantum fluctuations. Tilting the dipoles tunes the anisotropy of the dipole-dipole interaction and offers the possibility to trigger a spatial density modulation. In this work we combine those two aspects and investigate the formation of a self-bound and striped phase, which has been realized in experiments with actual dipolar droplets. We use a variational method based on the hypernetted-chain Euler-Lagrange optimization of a Jastrow-Feenberg ansatz for the many-body wave function to study the ground state properties of the system. This method takes into account quantum fluctuations in a non-perturbative way and is capable of describing strongly correlated systems. We also perform exact diffusion Monte Carlo simulations for comparison.

17:00 Switching a monolayer atomic mirror using a single Rydberg atom

Understanding and tuning light-matter interactions at the level of single quanta is essential for numerous applications in quantum science. Such quantum control seeks to increase the small interaction cross section between single atoms and single photons. Exploiting cooperative response of subwavelength atomic arrays allows for realizing strong light-matter coupling even down to the level of single photons. Here, we control the optical response of an atomically thin mirror using a single ancilla atom excited to a Rydberg state, that is, we use a single atom to control light at the single-photon level. The switching behavior is controlled by admixing a small Rydberg amplitude to the atomic mirror and therefore inducing strong dipolar Rydberg interactions with the ancilla. Driving coherent excitations of the ancilla atom, we demonstrate coherent control over the degree of transmission and reflection. Finally, increasing the mirror size directly reveals a spatial effective “switching” area around the ancilla. Our results pave the way towards novel quantum metasurfaces, the creation of controlled atom-photon entanglement and deterministically engineering quantum states of light.

17:00 Systematic effects in eEDM searches with BaF

A promising way to explore physics beyond the Standard Model of particle physics is doing high-precision measurements on molecules. One such measurement is the search for the P,T-violating electric dipole moment of the electron (eEDM). In diatomic molecules with one heavy atom, the effect of the eEDM is expected to be strongly enhanced, because of small rotational splittings and an enhanced electron density near a highly charged nucleus, with currently the best limit of $d_e<1.1×10^{-29}$ e cm measured in ThO [1]. In the NL-eEDM collaboration, the eEDM induced contribution to the ground state of BaF is investigated [2]. The eEDM manifests itself as an extra splitting between the magnetic substates due to the electric field, in addition to the Zeeman effect in magnetic fields. To measure the effect of a possible eEDM, a spin precession experiment is set up in well-controlled electric and magnetic fields. We use a two-photon transition to create a superposition of two hyperfine substates. In the magnetic and electric field, a phase difference between the two hyperfine states is accumulated, which has an extra contribution due to the electric field if the eEDM exists. The contributions to this phase from known-physics, in particular from the magnetic moment, require understanding of the molecular structure. The derived value for the eEDM is limited by statistics and the understanding of systematic effects.
To increase the statistical sensitivity, an intense source of ultracold BaF molecules will be used, produced in a cryogenic source. The molecules will be transversely laser cooled and decelerated with a Stark decelerator [3].
To have control over the systematics, it is crucial to understand how the eEDM signal depends on the experimental parameters, such as the magnetic field and laser intensities. For this we developed a description of the dynamics of our spin-precession experiment, based on the Optical Bloch Equations. With this tool we can calculate to which precision we need to control and measure the experimental parameters during the experiment.

[1] ACME Collaboration. Improved limit on the electric dipole moment of the electron, Nature 562, 355–360 (2018).
[2] The NL-eEDM collaboration., Aggarwal, P., Bethlem, H.L. et al. Measuring the electric dipole moment of the electron in BaF. Eur. Phys. J. D 72, 197 (2018).
[3] P. Aggarwal, Y. Yin, K. Esajas, H. L. Bethlem, A. Boeschoten, A. Borschevsky, S. Hoekstra, K. Jungmann, V. R. Marshall, T. B. Meijknecht, M. C. Mooij, R. G. E. Timmermans, A. Touwen, W. Ubachs, and L. Willmann (NL−eEDMCollaboration) Phys. Rev. Lett. 127, 173201

17:00 Tests of King's Linearity in Ca+

We report progress towards a precise measurement of the isotope shifts in the $4^2$S$_{1/2} \rightarrow 3^2$D$_{3/2}$ 732 nm electric quadrupole transition in Ca$^+$. We perform correlation spectroscopy [1,2] on two co-trapped calcium isotopes. Simultaneous excitation of both ions using frequency sidebands derived from a single laser enables cancellation of common-mode laser phase noise and reduction of systematic uncertainties from laser frequency drift or magnetic field instabilities. Such measurements have the potential to exceed Hz-level precision. When combined with our prior exploration [3] of the ${4^2\textrm{S}_{1/2} \rightarrow 3^2\textrm{D}_{5/2}}$ transition isotope shifts in a King Plot, these measurements can enable exacting tests of King's linearity, offering a path toward probing new physics beyond the Standard Model and providing benchmarks for ever-improving theory of atomic and nuclear structure.

[1] M. Chwwalla et al, Appl. Phys. B $\mathbf{89}$, 483-488 (2007).
[2] T. Manovitz et al, Phys. Rev. Lett $\mathbf{123}$, 203001 (2019).
[3] F. W. Knollmann et al, Phys. Rev. A $\mathbf{100}$ 022514 (2019).

17:00 Time-dependent variational Monte Carlo study of the dynamic response of bosons in an optical lattice

We study the dynamic response of bosons in a one-dimensional optical lattice and obtain the dynamic structure factor $S(k,\omega)$ for perturbations in the linear regime, as well as the non-linear response to strong density perturbations [1]. In our work, we use a continuous description of the system. Based on the time-dependent variational Monte Carlo method (tVMC) [2], we simulate the time propagation of a parametrized many-body wavefunction responding to an external probe pulse. A Jastrow-Feenberg ansatz with single particle and pair correlation functions is used as the model wavefunction.
For deep optical lattices we can compare $S(k,\omega)$ to exact diagonalization results obtained on a lattice in the Bose-Hubbard limit. When considering shallow optical lattices, the influence of higher Bloch bands is observed, indicating that the treatment in continuous space is appropriate for simulating the dynamics of the system. The non-linear response to strong pulses, with amplitudes equal to the optical lattice depth and a fixed wave number, is also investigated. From the power spectrum of the density fluctuations we can again infer the full excitation spectrum, albeit broadened, due to higher harmonic generation. In addition, we use different pulse strengths to investigate the transition from linear to non-linear response. A remarkable feature of tVMC is that the full excitation spectrum can also be retrieved from the power spectrum of the density fluctuations due to the stochastic noise inherent in any Monte Carlo method, without applying an actual perturbation.

[1] M. Gartner, F. Mazzanti and R.E. Zillich, Time-dependent variational Monte Carlo study of the dynamic structure factor for bosons in an optical lattice, arXiv preprint arXiv:2202.07535 (2022).
[2] G. Carleo, F. Becca, M. Schiró and M. Fabrizio, Localization and Glassy Dynamics Of ManyBody Quantum Systems, Scientific Reports 2(1), 243 (2012)

17:00 Tomography of Feshbach Resonance States

Quantum phenomena that lead to the formation of long-lived collision complexes, such as scattering resonances play a central role in cold molecular collisions. These resonances are fundamental probes of the fine details of internuclear interactions and serve as a benchmark for current computational methods.
Here we present a joint experimental and theoretical study where we are able to generate and investigate the multi-channel decay of a Feshbach resonance state with quantum state-to-state resolution. Our method is based on the coincidence detection of electron/ion momenta in Penning ionization collisions between metastable noble gas atoms and neutral molecules. Here, in a single measurement, we obtain both the energy and the composition at the continuum of each resonance state. Such a tomography of the Feshbach resonance states provides several tens of quantum numbers per measurement. We show that our results deviate from a purely statistical approach where the probability to decay into each open channel scales as its degeneracy level.
We also present an experimental scheme for control of tomography of the Feshbach states which is based on the initial constraint of total angular momentum at the Ionization step of the dynamics. The latter is motivated by our recent observation of a partial wave resonance at the lowest state of relative angular momentum.

17:00 Topological Electromagnetic Effects and Higher Second Chern Numbers in FourDimensional Gapped Phases

Higher-dimensional topological phases play a key role in understanding the lower-dimensional
topological phases and the related topological responses through a dimensional reduction procedure.
In this work, we present a Dirac-type model of four-dimensional (4D) Z2 topological insulator (TI)
protected by CP-symmetry, whose 3D boundary supports an odd number of Dirac cones. A specific
perturbation splits each bulk massive Dirac cone into two valleys separated in energy-momentum
space with opposite second Chern numbers, in which the 3D boundary modes become a nodal
sphere or a Weyl semimetallic phase. By introducing the electromagnetic (EM) and pseudo-EM
fields, exotic topological responses of our 4D system are revealed, which are found to be described
by the (4+1)D mixed Chern-Simons theories in the low-energy regime. Notably, several topological
phase transitions occur from a CP-broken Z2 TI to a Z TI when the bulk gap closes by giving
rise to exotic double-nodal-line/nodal-hyper-torus gapless phases. Finally, we propose to probe
experimentally these topological effects in cold atoms.

17:00 Towards a Fermi Gas Microscope with Tunable Lattice Geometry

We report on experimental progress towards quantum gas microscopy of ultracold lithium-6 in low-noise optical lattices with tunable geometry. By overlapping a superlattice beam over a two-dimensional square lattice, our setup enables the site-resolved study of Fermi-Hubbard physics in triangular, hexagonal, dimerized and quasi-1D geometries. Such nonstandard bandstructures are believed to host a variety of exotic strongly correlated phases that are hard to characterize in condensed-matter systems, such as the proposed spin liquid state in the triangular lattice Hubbard model or the pseudogap phase of the square lattice model. Dynamically changing the lattice geometry further allows preparation protocols that may help reduce temperatures below the limits of current experiments. Together with low heating rates provided by technical improvements on lattice noise and stability, this may help reach the yet unexplored low-temperature regime of the Hubbard phase diagram.

17:00 Towards a new search for hadronic CP violation using ultracold assembled $^{223}$FrAg molecules

We present a new approach to search for hadronic CP violation by measuring the $^{223}$Fr nuclear Schiff moment in ultracold assembled FrAg (francium silver) molecules. The $^{223}$Fr nucleus is known to have octupole deformation that leads to a factor of ~300 enhancement in the size of its Schiff moment for a given strength of CP-violating hadronic interactions [1]. The observable CP-violating energy shift induced when electrons interact with the Schiff moment is further amplified (relative to the shift in Fr atoms) when $^{223}$Fr is bound in a strongly ionic molecule that produces a large internal electric field. Binding Fr and Ag forms such a polar molecule [2,3]. Furthermore, both atoms have alkali-like atom structures, making them accessible to laser cooling, controllable interactions via Feshbach resonances, and optical trapping. Recent calculations have shown that the FrAg electronic structure is highly amenable to optical transfer of molecules from weakly-bound magneto-associated “Feshbach molecule” states, into the rovibronic ground state [4]. Assuming experimental parameters for molecule number, nuclear spin coherence time, and detection efficiency that have already been demonstrated in other experiments that use ultracold assembled molecules, we project a factor of 1000 improvement in underlying CP-violating physics for the first generation of an experiment with $^{223}$FrAg. Work is underway to form a magneto-optic trap of silver and then study ultracold Ag-Ag scattering properties. We also present plans to laser cool francium using an offline source.

[1] Spevak, V., Auerbach, N., & Flambaum, V. V. (1997). Enhanced T-odd, P-odd electromagnetic moments in reflection asymmetric nuclei. Physical Review C, 56(3), 1357.
[2] Fleig, T., & DeMille, D. (2021). Theoretical aspects of radium-containing molecules amenable to assembly from laser-cooled atoms for new physics searches. New Journal of Physics, 23(11), 113039.
[3] Śmiałkowski, M., & Tomza, M. (2021). Highly polar molecules consisting of a copper or silver atom interacting with an alkali-metal or alkaline-earth-metal atom. Physical Review A, 103(2), 022802.
[4] Kłos, J., Li, H., Tiesinga, E., & Kotochigova, S. (2022). Prospects for assembling ultracold radioactive molecules from laser-cooled atoms. New Journal of Physics, 24(2), 025005.

17:00 Towards a strontium quantum gas microscope

Ultracold quantum gases of atoms or molecules have become an outstanding tool to create and study various quantum many-body systems. Thanks to their high degree of controllability, they can be considered as quantum simulators - special purpose analog quantum computers - to address specific problems. An important example is optical lattice systems, which enable the implementation of the Hubbard model and can be probed with single-site and single-atom resolution in quantum gas microscope experiments.
In our experiment at ICFO, Barcelona, we aim at the realization of an ultracold strontium quantum gas microscope and pursue several research directions. Particularly, the subwavelength spacing of an optical lattice together with the two-level system of strontium will present an ideal environment to study the collective effects of atom-photon scattering. Additionally, the large nuclear spin of the fermionic isotope will enable access to rich physics of SU(N≤10) Fermi-Hubbard systems. A high-NA imaging system will provide single lattice site resolution, whereas spin-dependent shelving in the clock state will offer spin-resolved imaging. In my poster, I give an overview of our new machine for ultracold strontium and discuss the further steps.

17:00 Towards a two-photon optical clock in calcium

Two-photon transitions in neutral atoms are attractive candidates for the development of compact and portable optical clocks. Such clocks can be used to search for dark matter and dark energy, to build a gravitational wave telescope, to perform ultra-precise surveys of the earth's gravitational potential, and to serve as the foundation for the new definition of the SI second. The Doppler- and recoil-free nature of two-photon transitions eliminates the need for confinement of the atoms at ultracold temperatures. Clock precision of $\delta \nu/\nu \approx 10^{-16}/\sqrt{\tau}$ can be achieved without the need for an optical lattice or ion trap, both of which would introduce Stark shifts. Although it was historically thought that large probe laser light shifts were inevitable due to the high laser power required to drive two-photon transitions, we have developed a system of magic polarization to eliminate this shift. We report on progress towards the observation of the $4s^2 \; ^1S_0 \rightarrow 3d4s \; ^1D_2$ two-photon clock transition at 915 nm in a cloud of freely-falling $^{40}$Ca atoms.

17:00 Towards Microwave Shielding of Ultracold SrF Molecules

Quantum degenerate gases of ultracold dipolar molecules present a promising platform for advances in quantum simulation, quantum chemistry, and searches for physics beyond the Standard Model. Direct laser cooling of dipolar molecules is one successful method for achieving ultracold temperatures. Currently, we use sub-Doppler $\Lambda$-enhanced gray molasses cooling to load SrF molecules into an optical dipole trap. We have trapped $\sim 160$ SrF molecules at temperatures as low as 15 $\mu$K in a 420 $\mu$K deep trap using this approach. However, any significant increase in the phase space density of our molecular gas will likely be limited by inelastic losses caused e.g. by the barrierless chemical reaction SrF + SrF $\rightarrow$ SrF$_2$ + Sr. Here we report our plans to surmount this challenge by using circularly polarized microwaves to create a repulsive interaction between the SrF molecules. We generate these microwaves by combining two orthogonal polarizations with controllable phase and amplitude offsets onto an orthomode transducer, and then deliver them to the molecules via a conical horn and ellipsoidal mirror. Successful implementation of this scheme should clear a path to achieving a quantum degenerate gas of SrF molecules.

17:00 Towards strong photon-photon interactions via cold atoms trapped near a slow-mode photonic crystal waveguide

Trapping cold neutral atoms in close proximity to nanostructures has raised a large interest in recent years, pushing the frontiers of cavity-QED and boosting the emergence of the waveguide-QED field of research. Such platforms interfacing trapped cold atoms and guided light in nanoscale waveguides are a promising route to achieve a regime of strong coupling between light and atoms [1].
In this context, we propose to interface ⁸⁷Rb atoms with a GaInP waveguide based on a 2D photonic crystal waveguide (PCW) [2]. The periodic arangement of holes allows to shape the dispersion relation and engineer slow-modes [3], whose interaction with quantum emitters would be enhanced, allowing for strong coupling even in single pass. At the same time, guided modes are used to form dipole traps for the atoms, a crucial requirement for achieving strong coupling. The coupling of the atoms to the waveguide can be characterized by the Purcell factor, which relates the decay rate of the atoms into the guided mode to the one into free space. At realistic distances ∼ 100 nm from
the waveguide surface, FDTD calculations reveal that Purcell factors as high as 5 can be expected.
Moreover, dispersion engineering by tuning the geometrical parameters of the PCW can lead to a constant group index ng ∼ 30 over a range of 15 nm, centered around λ_Rb,D2 = 780 nm, making the design more robust to fabrication imperfections. We introduce a stable trapping scheme around our PCW for ⁸⁷Rb atoms based on an evanescent two-color dipole trap formed by fast guided modes.
This configuration was computed thanks to nanotrappy [4], a Python package developed by our group, to design, calculate and optimize dipole traps around nanoscale waveguides, making the search process faster and more systematic. Experimental realization of the cold atoms system is ongoing and promising first structures are being characterized.

[1] D. E. Chang, et al., Rev. Mod. Phys., 90, 031002 (2018)
[2] X. Zang, et al., Phys. Rev. Appl., 5, 024003 (2016)
[3] R. D. Meade, et al., Photonic crystals: Molding the flow of light (2008)
[4] J. Berroir, A. Bouscal, et al., Phys. Rev. Research, 4, 013079 (2022)

17:00 Transport in the 2D Fermi-Hubbard model: Lessons from weak coupling

Recent cold atom experiments have observed bad and strange metal behaviors in strongly-interacting Fermi-Hubbard systems. Motivated by these results, we calculate the thermoelectric transport properties of a 2D Fermi-Hubbard system in the weak coupling limit using quantum kinetic theory. We find that many features attributed to strong correlations are also found at weak coupling. In particular, for temperatures $T>t$ the electrical resistivity is nearly linear in temperature despite the fact that the quasiparticle scattering rate is non-linear and changes by nearly an order of magnitude. We argue that this asymptotic behavior is a general feature of systems with a finite spectral width, which implies that there is no MIR bound on the resistivity in single-band models. Due to nesting, the $T$-linear resistivity persists down to $T=0$ at half filling. Our work sheds light on the transport regimes accessible in ultracold atom experiments, which can differ substantially from that of condensed matter systems. Disentangling these band-structure effects from the physics of strong correlations is a major challenge for future experiments.

17:00 Tunneling Times and Interaction-Driven Spin Rotations in a Two-component BEC

How much time does a tunneling particle spend in a barrier? A Larmor clock, one proposal to answer this question, measures the interaction between the particle and the barrier region using the spin degree of freedom of the particle to clock the dwell time inside the barrier. We report on precise Larmor time measurements of a Bose-Einstein condensate of 87Rb atoms tunneling through an optical barrier. We observe that atoms generally spend less time tunneling through higher barriers and that this time decreases for lower energy particles, confirming longstanding predictions of tunneling times. In addition, we present evidence of spin waves generated in the reflected portion of the condensate. Due to the coincidence of scattering lengths in 87Rb, a BEC in a mixture of two hyperfine states behaves as a phase-coherent yet distinguishable two-component fluid. Reflection from the barrier creates a counter-propagating matter wave with spin partly transverse to the spin of the forward-going wave, initiating interaction-driven rotations due to the different interaction energies experienced by parallel versus anti-parallel spins. We observe one oscillation of a spin wave for low Rabi frequencies and study the transition where spin rotations become independent of the external coupling and instead are dominated by the interaction-driven effects.

17:00 Unitary fermionic p-wave interactions in a 3D optical lattice.

Resonantly enhanced and controllable p-wave interactions in ultracold atomic systems are a promising test bed for realizing unconventional superconductors and superfluids with non-trivial transport properties. However, p-wave and other antisymmetric interactions are weak in naturally occurring systems, and their enhancement via the Feshbach mechanism has been limited by three-body loss. Here, we report on spectroscopic measurements of Feshbach-enhanced p-wave interactions of $^{40}$K, where three-body loss is suppressed by loading pairs of spin polarized atoms into a multi-band 3D optical lattice. Our measurements extend up to the unitary limit characterized by a diverging p-wave scattering volume. These measurements show excellent agreements to an exact solution for two harmonically confined atoms interacting via a p-wave pseudopotential, and to numerical solutions using an ab-initio interaction potential. We also demonstrate the coherence of the conversion process between non-interacting and strongly interacting atomic pairs by measuring Rabi oscillations. Furthermore, we demonstrate that losses of p-wave interacting pairs are limited by the intrinsic lifetime of the free-space molecular dimer, and we observe lifetimes that are fifty times larger than previous measurements in $^{40}$K.

17:00 Update of the JILA Gen. II eEDM Experiment

Increasingly precise measurements of the permanent electric dipole moment of the electron (eEDM) probe physics beyond the standard model and shed light on open questions such as the baryon asymmetry and dark matter. Our measurement of the eEDM uses a thermal cloud of HfF+ ions held in an RF trap, allowing us to leverage second-scale coherence times and the large internal electric fields present in polar molecules. In this poster I present the final stages of the second generation measurement and discuss key systematic effects in the experiment.

17:00 Vector magnetometry with microwave-assisted optical pumping in warm Rb atoms

We report a microwave assisted optical vector magnetometer. Our method is based on the frequency difference and relative amplitudes of microwave-optical double resonances for different magnetic dipole transitions. Two hyperfine levels of $^{87}{\rm Rb}$ ground state are coupled strongly by a microwave field inside a cylindrical microwave cavity. A strong pump beam connects F = 2 [ground state] to F ′ = 2 [excited state], while a microwave field of frequency ω_μ pumps atoms between |1⟩ = |F = 1, m1⟩ and |2⟩ = |F = 2, m2⟩. The orientation of the microwave field with respect to the static field affects the amplitude of the double resonance peaks due to the polarization of the transitions, which provides us with information about the direction of the static field.

17:00 Wave turbulence in a homogenous 2D Bose gas

Turbulence is a multi-scale phenomenon, found in systems ranging from non-linear optics to the dynamics of the early universe. While turbulence escapes a complete microscopic understanding it is commonly associated with cascades, transporting system-specific conserved quantities, across different length scales.

Here, we employ a two-dimensional and homogenous ultracold Bose gas – a system with a high degree of experimental tunability – to study wave turbulence. A time-varying magnetic field gradient is used to excite a longest wavelength phonon mode, which under strong driving forms a direct energy cascade from low wavenumbers to high wavenumbers, where the dissipation scale lies. Using complimentary techniques, the system is probed on all length and time scales providing a view from individual quantum states to the full momentum distribution. We reveal two major theoretical cornerstones of turbulence formation: the establishment of the isotropic direct cascade, characterised by a power law, under anisotropic forcing; and the spatiotemporal scaling of the momentum distribution at times before any energy dissipation.

Rather than simply driving the longest wavelength mode, we are also able to excite shorter wavelength modes lying at intermediate wavenumbers using a Digital Micromirror Device. In this scenario, a dual system of two cascades where energy propagates to higher wavenumbers and particle number to lower wavenumbers is expected.

--

https://arxiv.org/abs/2203.09514

Wednesday 20 July

08:00 → 08:45 Exhibitors: Exhibitor Show Hours 8am-5:30pm

Exhibitors and vendors available

08:00 → 08:45 Registration / Info Desk open 8:00am-5:30pm

08:45 → 10:30 Plenary session

10:30 → 11:00 Coffee break

11:10 → 12:20 Plenary session

12:45 → 13:45 ICAP x TRIUMF: ICAP x TRIUMF session

Stimulated by new prospects for AMO precision studies at accelerator facilities, ICAP will feature a crossover session with this year’s TRIUMF Science Week, being held concurrently in Vancouver. This ICAP x TRIUMF session will showcase achievements and opportunities for atomic and molecular physics pursued by the TRIUMF community. The hope is to spark new connections and explore research at the intersection of accelerator-based science and AMO physics. The session will be live-streamed to room WO025 at Woodsworth College Residences, which is 5 minutes' walk from the RCM. For more information, see "Satellite events" page.

Convener: Prof. Amar Vutha (University of Toronto)

14:00 → 15:10 Plenary session

15:10 → 15:40 Coffee break

15:50 → 17:00 Plenary session

17:00 → 18:30 Poster session: Wednesday

17:00 A cold atom gyroscope for inertial navigation

Many sectors of society and the economy are now heavily reliant on Global Navigation Satellite Systems (GNSS). However, GNSS has several intrinsic vulnerabilities and cannot be used underwater or underground. In these situations, Inertial Navigation Systems (INSs) can act as a reliable alternative. These self-contained devices reconstruct the trajectory of a vehicle being tracked by measuring its acceleration and rotation rate. A complete INS combines measurements from three orthogonal accelerometers and three orthogonal gyroscopes. Together with knowledge of the vehicle's starting position, its current location can be calculated, without the need for an external reference. Conventional systems use high precision classical sensors, however long-term performance is currently limited by scale factor and bias drifts.

At Imperial College we are developing cold atom interferometers for inertial sensing. Their high-accuracy and long-term stability mean they offer the potential for improved long-range navigation in the near future. Clouds of rubidium-87 atoms are cooled to ultra cold temperatures then split, reflected, and recombined using stimulated Raman transitions to make an atom interferometer. Here, we describe our recent work to extend the operation of our laboratory, two-axis accelerometer into a rotation sensor. By launching the atom cloud using a moving molasses, we are able to measure rotations about three perpendicular axes.

17:00 A cryogenic neutral atom optical tweezer array

Scalable ultracold Rydberg atom arrays provide an intriguing platform for programmable quantum computation. We present a new system for a 2D Rydberg qubit array of 87Rb atoms embedded in a low-vibration cryostat. Cryopumping will improve the atom vacuum lifetime to fully leverage the scalability of Rydberg platforms, and a 30 K environment will extend the Rydberg lifetime to several times its value at room temperature. To create a large and controlled array, we will utilize a 2D optical lattice with the site-resolved addressability and interaction control aided by optical tweezers. We will harness a bi-chromatic magic lattice to provide identical confinement for both ground and Rydberg states. We will report our results on cryocooling and vibration isolation performance, as well as our progress towards atom trapping within the cryogenic environment.

17:00 A new experiment on atomic tweezer arrays in a cryostat

Optical-tweezer arrays are a powerful platform for realising analog and digital quantum simulators. However, they share the scalability problem common to all quantum hardware. Here, we present a new experimental setup that integrates the tweezer technology in a cryogenic environment. At 4K, we are able to measure a vacuum-limited lifetime of more than 6000 seconds, which represents a two-order-of-magnitude improvement over room temperature setups [1]. In addition, we have implemented an optimised trap loading equalisation procedure that, in combination with the extended lifetime, allows us to build arrays with more than 300 atoms while maintaining high accuracy of defect-free realisations.
These results are the first step towards Rydberg quantum simulators with more than a thousand particles.

[1] Kai-Niklas Schymik, Sara Pancaldi, Florence Nogrette, Daniel Barredo, Julien Paris, Antoine Browaeys, and Thierry Lahaye, Single Atoms with 6000-Second Trapping Lifetimes in Optical-Tweezer Arrays at Cryogenic Temperatures, Phys. Rev. Applied 16, 034013 (2021)

17:00 A Quantum Gas Microscope for RbCs and KCs Rovibration Ground State Molecules

Quantum gas microscopes are a powerful tool which can be used study particles confined to an optical lattice. By fluorescing trapped particles under an objective with a high numerical aperture it is possible to obtain single site resolution of the optical lattice. This has already been demonstrated with atoms and has paved the way for a novel platform for simulation experiments for lattice potentials. However, in optical lattices atoms have poor interactions between neighbouring sites. Here, we present our progress towards a quantum gas microscope for RbCs and KCs molecules. With molecules the issue of poor interactions is mitigated owing to the dipole - dipole interactions exhibited by molecules in neighbouring sites allowing us to more readily probe the relevant terms in the lattice Hamiltonian.

17:00 A transportable Yb optical lattice clock

Optical lattice clocks have demonstrated fractional uncertainty and instability at the $10^{-18}$ level and beyond. At this performance level, such systems become useful for applications including tests of general relativity, searches for dark matter, time-resolved measurements of geophysical phenomena such as Earth tides, and remote comparisons between distant metrological institutes. However, these systems typically span one or more rooms and are staffed by several experts during clock operation. We present a transportable Yb optical lattice clock which occupies only approximately 1000L and seeks to achieve high autonomous uptime through a suite of advanced controls systems. Preliminary comparisons against a laboratory clock demonstrate an instability near $10^{-17}$ at 1000 seconds. Several key systematics for transportable operation have been analyzed at the $10^{-18}$ uncertainty level, and a full uncertainty budget will be completed in 2023. We highlight several upcoming applications including a possible test of general relativity on a >4000 m mountain summit using two-way optical time and frequency transfer to compare with laboratory clocks at NIST.

17:00 Accurate and complete atomic data set for helium-like ions using Relativistic Configuration Interaction approach for singly and doubly excited states with Z = 5 - 9

Accurate atomic data is considered to be the principal way to effectively solve the future energy problem as a clean and infinite energy resource and it is being developed internationally via the International Thermonuclear Experimental Reactor $(ITER)$ Project [1]. Then, extensive spectroscopic studies both experimental and theoretical have been performed in the last few years in order to estimate the power loss from the impurities in the forthcoming fusion reactors. Furthermore, accurate values of wavelengths and their errors are required for the interpretation of a wealth of high-resolution data obtained in the last two decades by the Chandra X-ray Observatory and the European Space Agency's X-ray Multi-Mirror Mission.
As previously published [2, 3], we continue to focus on helium-like ions. In this work, energy levels, wavelengths and transitions rates have been calculated for the lowest singly excited 70 levels among $ 1snl (n\leq 6, l \leq (n-1)) $ configurations and the lowest doubly excited 250 levels arising from the K-vacancy $2ln'l' (n'\leq 6,\:l' \leq (n'-1))$ configurations of helium-like ions with $Z = 5-9$ namely $B\: IV$, $C \:V$, $N \:VI$, $O \:VII$ and $F \:VIII$ [4]. The calculations were performed using the Relativistic Configuration Interaction $(RCI)$ method implemented in the Flexible Atomic Code $(FAC)$ [5]. Comparisons were made with other available theories reported in the literature [6, 7, 8, 9]. Finally, the accuracy of the present calculations is enough to facilitate the identification of many observed spectral lines, plasma modelling as well as diagnostics of astrophysical plasma and controlled thermonuclear fusion.

References
[1] A J H, Donne et al, Nucl. Fusion. 47, 337 (2007).
[2] S Manai and H Jelassi, Pramana. 95, 1-9 (2021).
[3] S Ben Nasr, S Manai, D E Salhi, P Quinet and H Jelassi, Atomic Data and Nuclear Data Tables. 135, 101346 (2020).
[4] S Manai, D E Salhi, S Ben Nasr and H Jelassi. Results in Physics. 37, 105487 (2022).
[5] M. F. Gu, Canadian Journal of Physics. 86, 675-689 (2008).
[6] G. W. Drake, Canadian Journal of Physics. 66, 586611 (1988).
[7] D A Verner, E M Verner and G J Ferland, Atomic Data and Nuclear Data Tables. 64, 1180 (1996).
[8] K M Aggarwal, T Kato, F P Keenan and I Murakami, Physica Scripta. 83, 015302 (2010).
[9] B Sow, M Sow, Y Gning, A Traore, A S Ndao and A Wague, Radiation Physics and Chemistry. 123, 2530 (2016).

17:00 An eEDM sensitive experiment using BaF molecules

Searches limiting the value of the permanent electric dipole moment on the electron (eEDM) are a sensitive probe of the Standard Model of particle physics and its extensions. Such searches have been performed in a number of different atoms and molecules, which resulted in the best current limit on the eEDM of $|d_e| < 1.1 \times 10^{-29}~\rm{e~cm}$ [1]. Our experiment has been setup with a BaF supersonic beam with velocities of $\approx600~\rm{m/s}$. The sensitivity towards an eEDM requires a phase sensitive spin precession measurement in well-known E- and B-fields (10 kV/cm, 10 nT resp.) [2]. The superposition state of the $|F=0 , m_F = |1|>$ magnetic substates in the $𝑋^2Σ^+ (𝜈 = 0, 𝑁 = 0)$ ground state of BaF is created and read out solely by pulsed laser field interactions. The resulting spin precession signal depends on laser field parameters such as intensity, polarization and frequency detuning. We experimentally investigated the dependence on these parameters which are indispensable for quantification of possible systematic biases that could arise on the eEDM limit extracted limit. We aim to complete an initial measurement stage at a sensitivity level $10^{−28}~\rm{e~cm}$ within this year.

[1] ACME Collaboration, Nature 562, 355–360 (2018).
[2] The NL-eEDM collaboration, Eur. Phys. J. D 72, 197 (2018)

17:00 Ancillary transitions in $^{171}$Yb$^+$ ion clocks for shift evaluation and tests of fundamental physics

$^{171}$Yb$^+$ ions feature two optical clock transitions: an electric quadrupole (E2) transition at 436 nm and an electric octupole (E3) transition at 467 nm. These two transitions have very different properties due to the different electronic structure of their excited states. In particular, they have a large differential sensitivity to the fine structure constant α, so that tight limits on possible variations can be obtained by comparing their frequencies at various positions in spacetime [1].

Of the two transitions, the E3 transition ($^2$S$_{1/2}$, F=0 – $^2$F$_{7/2}$, F=3) is particularly suitable for precision spectroscopy: Its excited state features a yearslong natural lifetime [2], so that coherent interrogation times are not limited by the spontaneous decay. Additionally, the excited state sensitivity to external electric and magnetic fields is almost equal to that of the ground state, resulting in a weak differential dependence for the transition. This permits high accuracy in the realization of the unperturbed E3 transition frequency [3].

The E2 transition ($^2$S$_{1/2}$, F=0 – $^2$D$_{5/2}$, F=2), on the other hand, features a larger sensitivity to external fields, which makes it a suitable ancillary transition: Residual perturbing fields are investigated on a magnified scale and can improve the knowledge of the unperturbed E3 transition frequency when relative sensitivities are known [4]. However, the E2 transition coherent interrogation is limited to about 40 ms by the relatively short lifetime of its excited state.

Additional ancillary transitions without this limitation are provided between the F=3 and F=4 hyperfine states of the long-lived $^2$F$_{7/2}$ state and their Zeeman manifolds (in a static external magnetic field). We drive these transitions using microwave radiation at about 3.6 GHz to investigate magnetic field and tensor frequency shifts. Microwave spectroscopy is not limited by ion heating and finite laser coherence, which makes it a useful tool to resolve small frequency shifts within a short measurement time. We obtain coherent interrogation times exceeding 5 s, allowing us to resolve mHz shifts within hours. Dynamical decoupling pulse sequences can be used to coherently average the energy of ±m$_\text{F} $ Zeeman pairs. This suppresses the linear Zeeman shift and associated energy fluctuations while retaining sensitivity to frequency shifts depending on m$_\text{F}^2 $, including possible shifts due to violations of local Lorentz invariance.

[1] R. Lange , N. Huntemann , J. M. Rahm , C. Sanner, H. Shao, B. Lipphardt , Chr. Tamm, S. Weyers , and E. Peik, “Improved Limits for Violations of Local Position Invariance from Atomic Clock Comparisons”, Phys. Rev. Lett. 126, 011102 (2021).
[2] R. Lange, A. A. Peshkov, N. Huntemann, Chr. Tamm, A. Surzhykov, and E. Peik, “Lifetime of the 2F7/2 Level in Yb+ for Spontaneous Emission of Electric Octupole Radiation”, Phys. Rev. Lett. 127, 213001 (2021).
[3] C. Sanner, N. Huntemann, R. Lange, Chr. Tamm, E. Peik, M. S. Safronova, and S. G. Porsev, “Optical clock comparison for Lorentz symmetry testing“, Nature 567, 204 (2019).
[4] R. Lange, N. Huntemann, C. Sanner, H. Shao, B. Lipphardt, Chr. Tamm, and E. Peik, “Coherent Suppression of Tensor Frequency Shifts through Magnetic Field Rotation”, Phys. Rev. Lett. 125, 143201 (2020).

17:00 Arrays of Cold Rydberg Atoms for Electromagnetic Fields Sensing

We aim to develop a new kind of electromagnetic field sensor by combining the high metrological performance accessible thanks to the exaggerated Rydberg states properties with the high degree of control and tunability offered by cold atomic ensembles trapped in arrays of optical tweezers. We plan to probe EM-fields over a wide frequency range from few 100s of MHz to few THz, given by the frequency difference between neighboring Rydberg states, with a target sensitivity of about 10 mV/cm/Hz$^{1/2}$ and with a spatial resolution down to few tens of µm, corresponding to the distance between two optical tweezers. We also intend to study the possibility to perform spectral analysis by making each atomic ensemble sensitive to a specific frequency. In the poster I will present the principle of operation of the sensor, the current experimental status together with some envisioned applications and possible ways of improvements.

17:00 Atom Camera: Super-resolution imaging of an optical field with a single ultracold atom in an optical tweezers

In a cold-atom experiment with an optical tweezers array, a laser beam with a designed wavefront is focused through a high numerical-aperture objective lens to form an arbitrarily shaped light pattern on the focal plane in a vacuum chamber [1, 2, 3]. Accordingly, the pattern is often deteriorated by aberrations in optical components and thereby should be monitored and evaluated in situ. However, it is difficult to do so due to the difficulty of accessing the focal plane in a vacuum chamber.

We will report on an “atom camera” method that we have developed for imaging the light pattern with a single $^{87}$Rb atom in an optical tweezers. We sense the intensity and polarization profiles of a light pattern at the atom position that manifest themselves in the light shift of the hyperfine transition. By scanning the atom position in steps of sub-micrometers, we reconstruct high-resolution 2D images of the intensity and polarization. The resolution is limited only by the uncertainty of the atom position, which is reduced down to the level of quantum fluctuations (~ 30 nm) by cooling the atom to the motional ground state of the tweezers [3], thus far better than the diffraction limit at optical wavelengths. This technique serves as an important tool for the design and evaluation of submicron-scale light patterns.

[1] A.Browaeys and T. Lahaye, Nat. Phys. 16, 132-142 (2020).
[2] F. Nogrette et al., PRX 4, 021034 (2014).
[3] Y. Chew et al., arXiv: 2111.12314.

17:00 Atomic magnetometry with Kalman Filters

Information inference from noisy systems is a focus of interest of various research and engineering disciplines. In 1960, Rudolf E. Kalman published a paper on an optimal filtering technique for systems described by linear dynamics and measurement models whose noise statistics is Gaussian [1]. In particular, this so-called Kalman Filter constitutes a way to construct an estimator that allows one to optimally extract the signal encoded in the system dynamics while minimizing the average mean-squared-error, despite the dynamics and measurement all undergoing uncontrolled independent stochastic fluctuations. In opposition to previously known algorithms, Kalman Filters do not require a full history of all previous steps. Because of this the technique can be used for real-time data analysis.

In this work, we applied the described methods for magnetic field inference from an atomic sensor with optical read-out.
Such sensors are widely used in magnetometry both within and beyond the classical limit, achieving precision comparable to cryogenic methods. The linear Kalman Filter has been applied to such systems before [2, 3]. The usability of this technique is very limited though, as the magnetic field obeys a highly non-linear dynamics in most regimes. This suggests that using the Extended Kalman Filter as well as other non-linear Kalman Filtering techniques can greatly improve the estimator beyond the linear regime. In this work, we simulate an output of such a sensor and show that in fact the magnetic field can be successfully estimated in real-time with the non-linear methods.

[1] R. E. Kalman, A New Approach to Linear Filtering and Prediction Problems, Journal of Basic
Engineering, vol.81, 1960.
[2] Ricardo Jiménez-Martínez et. all Signal Tracking Beyond the Time Resolution of an Atomic
Sensor by Kalman Filtering, PRL, vol. 120, 2018
[3] Jia Kong et. all Measurement-induced, spatially-extended entanglement in a hot, strongly-
interacting atomic system, Nature Communications vol. 11, Article number: 2415, 2020.

17:00 Atomic mass ratios of the proton, deuteron, triton and helium-3

The Florida State University cryogenic Penning ion trap has previously produced the most precise values of the masses of heavier atoms required for several important atomic physics applications [1]. These include Rb and Cs for atom-interferometric measurement of h/m for the fine structure constant, and isotopes of Sr and Yb for King plot analyses. More recently we have focused on mass ratios between isotopes of hydrogen and helium. The relative masses of the proton, deuteron, triton and helion are fundamental constants impacting several areas of physics. In particular, a high-precision value for the mass difference between tritium and helium-3 is important for testing systematics in the ongoing KATRIN neutrino mass experiment, while the deuteron/proton mass ratio is important for interpreting the results of recent high-precision laser and terahertz spectroscopy of the HD+ molecular ion, leading to an improved value of the electron/proton mass ratio or, alternatively, limits on beyond-standard-model nucleon-nucleon interactions [2]. We achieve high precision by measuring the cyclotron frequency ratio of a pair of ions simultaneously trapped in a single Penning trap. For most of our measurements we alternate each ion between the center of the trap, where its cyclotron frequency is measured, and a large cyclotron “parking” orbit. Our previous measurements on mass-3 ions, besides providing the important Q-value for KATRIN, revealed significant errors in previously accepted values for the masses of p, d and h. In the case of measurements of H2+ against D+, we achieved sufficient resolution to distinguish different vibrational levels of H2+ by their difference in mass, and also to observe vibrational Stark quenching [3]. We then placed an H2+ and D+ in a coupled magnetron orbit and measured their cyclotron frequencies simultaneously [4]. This suppressed the effect of variation in the magnetic field by several orders of magnitude. It also reduced uncertainty related to measurement of the ions’ axial frequencies. Using this technique we partly resolved H2+ rotational energy through the change in mass. This resulted in a value for the deuteron/proton mass ratio at 5 ppt and the first proton atomic mass at 10 ppt.
[1] E.G. Myers, Int. J. Mass Spectrometry 349-350, 107 (2013).
[2] S. Patra, et al., Science, 369 (6508), 1238 (2020).
[3] D. J. Fink and E. G. Myers, Phys. Rev. Lett. 124, 013001 (2020)
[4] D. J. Fink and E. G. Myers, Phys. Rev. Lett. 127, 243001 (2021)

17:00 B-field self-cancelling devices for atomic sensors

A fair number of atomic sensors require a homogeneous B-field for long-lasting Larmor oscillation of atoms. On the other hand, various electronics used in the experients emit magnetic fields, destroying the homogeneity of the deliberately homogeneous B-field. We demonstrate a DBR laser-TEC packaging and a heater which self-cancel their emitted B-field by antiparallel current configurations. These devices can be realized inexpensively without employing MEMS technology. The effect of the self-cancellation is demonstated by a direct measurement and also a LIA signal noise comparison for the heater employed in an atomic magnetometer system.

17:00 Barium-monofluoride within an argon solid: Calculations to support the EDMcubed scheme for measuring the electron electric dipole moment

The EDMcubed collaboration is working towards a measurement of the electric dipole moment of the electron (eEDM) using barium-monofluoride (BaF) embedded in an argon solid. The large numbers of embedded BaF in this measurement scheme [1] gives the potential for a very precise eEDM measurement. In this work, we present precise relativistic electronic structure calculations (all-electron, with an extrapolation to a complete basis set) of the BaF-Ar tri-atomic system, for a wide range of BaF-Ar separations and angles. The resulting BaF-Ar potential can be parameterized and used to model a BaF molecule embedded into an Ar solid to determine the structure of the local environment around the BaF molecule.

[1] A. C. Vutha, M. Horbatsch and E. A. Hessels, Phys. Rev. A 98, 032513 (2018).

17:00 Blueprint for a scalable, modular, fault-tolerant quantum computer based on state-of-the-art Rydberg atom arrays and optical cavities

We propose a scalable, modular, fault-tolerant architecture for quantum computing based on Rydberg arrays and Rydberg compatible optical cavities. While previous modular architectures have focused on very small modules containing 2-5 qubits, our architecture consists of large modules containing thousands of physical qubits, which form surface code patches that are linked together by optical cavity photonic interconnects. While the low fidelity of Bell pairs generated via photonic interconnects has been a major challenge for all previously proposed modular architectures, our approach is uniquely immune to Bell pair infidelity because communication errors only occur along one edge of the code. Numerical simulations indicate a threshold for communication errors of about 10%. Moreover, because no distillation is required, in contrast to previous schemes, local gate requirements remain around 1%. These relaxed communication requirements enable the fault-tolerant connection of currently available Rydberg arrays of many atoms using only modest quality Bell pairs. We give quantitative performance estimates showing that a single optical cavity of modest quality allows Bell pair distribution fast enough to realize 10 kHz surface code cycles—much faster than current coherence times—as well as sufficiently fast syndrome readout and atom reloading.

17:00 Breakdown of topological transport in a Hubbard-Thouless pump

The fate of topological transport in the strongly correlated regime raises fundamental questions on the role of geometry in quantum many-body physics. A paradigm of quantised transport is the topological Thouless pump, which represents the one-dimensional, dynamic analogue of the quantum Hall effect. A few experiments have explored the effects of interactions on Thouless pumping in two-body and optical mean-field systems, but the strongly correlated regime has so far remained out of reach. Here, we experimentally detect the breakdown of topological transport due to strong Hubbard interactions in a fermionic Thouless pump, facilitated by a dynamical optical superlattice. We observe the deviation from quantised pumping for repulsive Hubbard U, which we attribute to pinned atoms in a Mott insulator. On the attractive side another mechanism is reducing the pumping efficiency: a smaller energy gap for pair pumping makes the evolution less adiabatic [1]. The dynamical superlattice operated at a single frequency establishes a novel platform for studying topology in the presence of strong correlations in one, two, and possibly three dimensions, including avenues to fractional transport.

17:00 Collective excitation and decay of waveguide-coupled atoms: from timed Dicke states to inverted ensembles

The collective absorption and emission of light by an ensemble of atoms is at the heart of many fundamental quantum optical effects and the basis for numerous applications. However, beyond weak excitation, both experiment and theory become increasingly challenging. Here, we explore the regimes from weak excitation to inversion with ensembles of up to one thousand atoms that are trapped and optically interfaced using the evanescent field surrounding an optical nanofiber. We realize strong inversion, with about 80% of the atoms being excited, and study their subsequent radiative decay into the guided modes. The data is very well described by a simple model that assumes a cascaded interaction of the guided light with the atoms. Our results contribute to the fundamental understanding of the collective interaction of light and matter and are relevant for applications ranging from quantum memories to sources of nonclassical light to optical frequency standards.

17:00 Conditions for superluminal light propagation in a three-level medium

The investigation of propagation of pulses in optically dressed media is one of the most basic problems in optics. I will analyze a new superluminal propagation regime in the ladder-type three-level systems near a two-photon resonance where an anomalous dispersion appears accompanied by a small absorption. These conditions are necessary to achieve group velocities greater than the speed of light in a vacuum $(v_g>c)$ or negative $(v_g<0)$. In order to achieve these conditions, previous works exploited population inversion, additional fields, and complicated level configurations. Here, I will demonstrate superluminality can be reached through a relatively simple scenario.

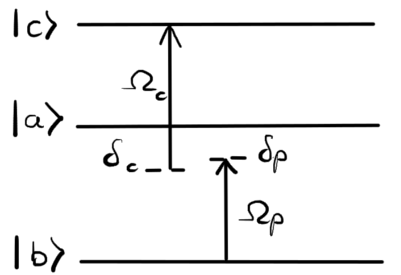
Our model is a one-dimensional medium consisting of three-level systems with the energy levels configuration sketched in Fig. 1. There are electric-dipole-allowed transitions $\vert b \rangle\to \vert a \rangle$ with an energy $\hbar\omega_{ba}$, $\vert a \rangle\to \vert c \rangle$ with an energy $\hbar\omega_{ac}$ and an electric-dipole-forbidden transition $\vert b \rangle\not\to \vert c \rangle$. The lower levels are coupled by the probe field $\Omega_p(z,t)$ (with carrier frequency $\omega_p$), and the upper ones are driven by the control field $\Omega_c(z,t)$ (with carrier frequency $\omega_c$). I will show that to establish the best performance we have to set $\delta_c$ to be hundreds of times greater than the width of the energy levels so we are far from the influence of the single-photon resonance.

In the numerical simulations, we chose a real-life example of rubidium vapor in a $L=5$ cm long cell well approximated by a one-dimensional model. To optimize the conditions for superluminal propagation in terms of the control field properties $\delta_c$, $\Omega_c$, we introduce the parameter
$\begin{equation*} %\label{eq:parameter} \beta(\delta_c, \Omega_c)=\left(1-\min_{\delta_p}(n_g(\delta_p, \delta_c, \Omega_c))\right)\left(e^{-\frac{\omega_{p}}{2c}\chi_{ab}(\delta^\text{min}_p, \delta_c, \Omega_c)L}\right)^4, \end{equation*}$
where $n_g$ is the group index (related to group velocity by the formula $v_g=c/n_g$) and $\chi_{ab}$ is the electric susceptibility of the medium. The left bracket simply maximizes group velocity in the given conditions while the right one describes absorption. The forth power forces absorption to be no more than 20% to prevent pulse distortions.

As a result, we come up with Fig. 2a where the greater the value of the parameter $\beta$, the better the superluminal conditions. The point for which we analyze the propagation in Fig 2b and 2c is marked with the white plus sign. We consider an input Gaussian pulse with the carrier frequency near two-photon resonance. Fig. 2b shows pulse shapes at the end of the sample for several detunings $\delta_p$ selected to be near two-photon resonance, and indeed, the absorption is limited as expected. Finally, in Fig. 2c, we have group index as a function of detuning $\delta_p$, hence, we have evidence that near the two-photon resonance superluminal propagation occurs as $n_g$ values are well below one (grey region).

In my contribution, I will present a more comprehensive discussion of superluminal propagation regimes.

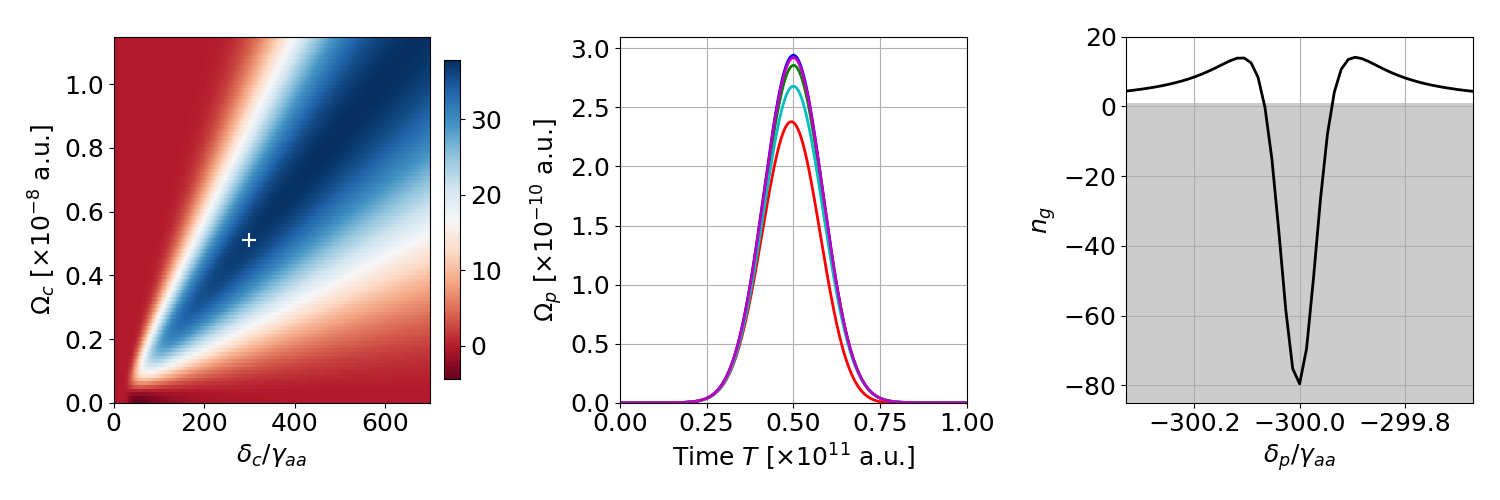
17:00 Controlling reactive interactions with ultracold magnetic molecules

We are realizing a new experiment for investigating and controlling ultracold chemical reactions. We plan to use mixtures of magnetic atoms and create molecular gases and atom-molecule mixtures with widely tunable interactions. Combining techniques from quantum optics and physical chemistry, we will develop new methods for shielding chemical reactions and stabilizing bosonic molecular gases.

17:00 Dicke superradiance and photon statistics in waveguide QED

Dicke superradiance is a phenomenon where atoms at an identical location synchronize and collectively emit photons in a short, bright burst. We investigate the many-body decay of an extended array of atoms coupled to a one-dimensional optical channel. We show that Dicke superradiance in waveguides is intrinsically different from superradiance in cavities and free space, as there are two distinct decay channels competing with each other. We derive the minimal condition for the burst to happen as a function of the number of atoms, the interatomic distance, and decay rates into the waveguide and non-guided modes. The existence of two decay channels gives rise to the creation of dark states in the few-excitation subspace. Exotic probability distributions for the emitted photons emerge: while the first photon is emitted randomly to the left or to the right, correlations imprinted on the array enhance the possibility of a subsequent photon to be emitted in the same direction, yielding an avalanche process. These results are relevant to current experiments in waveguide QED with cold atoms coupled to nanofibers and superconducting qubits coupled to transmission lines.

17:00 Emergence of hydrodynamics and pairing in a two-dimensional few fermion system

Fermionic quantum systems with a tuneable atom number have proven to be a viable platform for exploring the emergence of many-body phenomena. In our experimental setup we can deterministically prepare few-body fermionic quantum systems in a two-dimensional harmonic potential with stable closed-shell configurations.

Using a time-of-flight expansion in combination with our imaging technique, which provides spin and single atom resolution simultaneously, we can explore correlations of atoms in different spin states in momentum space. This has recently lead us to the observation of Cooper pairs (1). We have recently extended our imaging technique to real space, by magnifying the matterwave. Similar to technique demonstrated in (2), we have developed a matterwave optics technique to expand the wavefunction prior to fluorescence imaging. This allows us to resolve it with our existing imaging setup, giving us access to correlations and small structures in both real and momentum space.

We now utilize this expanded imaging scheme to investigate the emergence of hydrodynamic behaviour in dependence on particle number and interaction strength. By preparing closed shell configurations of an elliptic harmonic oscillator, we can directly observe the inversion of the aspect ratio at particle numbers as low as five atoms per spin state. Additionally, we see an enhancement of pair correlations after an interacting expansion. We directly study this formation of pairs by magnifying the real space wave function after different short interacting expansion times.

(1) Holten et al. arXiv: 2109.11511 (2021) accepted in Nature
(2) Asteria et al. Nature 599, 571-575 (2021)

17:00 Engineering Multimode Entanglement among Atomic Ensembles

Interactions form the basis for the experimental generation of entanglement between quantum objects. Using all-to-all interactions, numerous experiments with atomic ensembles have generated quantum states which provide a higher precision in sensing protocols compared to unentangled states. However, many envisioned applications in quantum sensing and computation require greater control over the spatial entanglement structure and, thus, the effective graph of interactions. In our experiment, we use an optical cavity together with local spin rotations to mediate programmable long-range interactions within a 1D array of atomic ensembles. Driving the cavity with light induces all-to-all interactions between the spin-1 atoms, creating atom pairs and quantum correlations within a single spatially extended mode of the collective transversal spin. In this case, we measure spin-nematic squeezing and verify the generation of entanglement between spatially separated ensembles by quantifying the correlations in two non-commuting observables. By employing local spin rotations we selectively couple different spatial modes to the cavity and thus control the structure of the generated quantum correlations. This capability allows for tailoring the entanglement structure to a specific quantum enhanced task such as distributed quantum sensing and measurement-based quantum computation.

17:00 Entanglement dynamics of bosons trapped in a 1D optical lattice

Quantum entanglement has attracted much attention in the study of quantum many-body systems because it plays important roles in various phenomena such as thermalization of isolated quantum systems. Especially, it is remarkable that the 2nd-order Renyi entropy (RE), which is a measure of entanglement, has been successfully measured in the system of bosons trapped in a 1D optical lattice.
$\quad$Motivated the experimental development, we study entanglement dynamics of bosons in a 1D optical lattice. Specifically, we calculate the time-evolution of the RE when the system is quenched from the deep Mott insulating (MI) regime. For quench within the MI regime, we derive the analytic expression for the time-evolution of RE and show that it oscillates with the period determined by the strength of the on-site interaction and finally converges to a certain value proportional to the subsystem size. On the other hand, for quench into the superfluid (SF) regime, RE does not oscillate but increases almost linearly and converges to a certain value that is also proportional to the subsystem size. We also show that the behavior of the 2nd-order RE exhibits distinct features depending of whether the system is quenched into the SF or MI phases. This implies that the signature of the SF-MI phase transition appears in the entanglement dynamics.

Speaker: Shion Yamashika (Chuo University)

17:00 Entanglement generation in multilevel atomic arrays with dipolar interactions

We investigate the driven-dissipative dynamics of 1D arrays of multilevel atoms interacting via photon mediated dipole-dipole interactions and trapped at subwavelength scales. In contrast to two-level atoms, we show that multilevel atoms in the low excitation (weak drive) regime can become strongly entangled. The entanglement arises from the action of a non-trivial effective Hamiltonian and jump operators that contain multi-body terms acting on the ground state manifold, and survives even after turning off the drive. We propose to use the $\sim 2.9 \mu$m transition between $\rm ^3P_2 \leftrightarrow \, ^3D_3$ in $\rm ^{88}Sr$ with $389$nm trapping light as an ideal experimental platform for validating our predictions and as a novel quantum interface for the exploration of complex many-body phenomena emerging from light-matter interactions.

17:00 Entanglement of the macroscopic spins of two spatially separated Bose-Einstein condensates

We experimentally investigate the entanglement of two spatially separated many particle systems. Our experiments are based on a two component pseudo spin-$1/2$ Bose Einstein condensate of $^{87}$Rb on an atom chip. By engineering the interatomic interactions through state dependent trapping we are able to produce entangled spin-squeezed states in this system. Using coherent spin manipulations we split this entangled many-particle state into two halves in spin space and magnetic field gradients allow us to separate the two two-component BECs spatially by more than 40 $\mu$m. Our technique allows us to individually address the collective spins of the two BECs after splitting thereby realizing arbitrary spin measurements on the two systems. Their correlations allow to infer measurement results of non-commuting spin observables in one system from measurements on the other, demonstrating the entanglement of the two Bose-Einstein condensed clouds of roughly 800 atoms each. Besides the interest in understanding fundamental aspects of entanglement of many-body systems, our experiments enable new investigations in quantum enhanced metrology using spatially split probes.

Speaker: Paolo Colciaghi (University of Basel)

17:00 Error budget in Cold Atom-based Inertial Sensors

Cold Atom-based technology promises a new generation of navigation systems potentially suitable for Global Navigation Satellite System-denied environments. However, despite the promise of superior inertial navigation capabilities, a correct identification and quantification of the errors must be carried out to assess what and how system parameters affect the sensor performance. In this context, sensitivity function represents a theoretical tool that allows to quantify the output of a Cold Atom-based Inertial Sensor in terms of scale factor, bias, and noise. As a result of time-dependent perturbation theory, the sensitivity function can be used to link quantum optimal control and Bloch sphere picture, thus enabling the design of tailored Raman beam-splitter pulses resilient to phase dispersion errors.

17:00 Evaluating states in trapped ions with local correlation between internal and motional degrees of freedom

We propose and demonstrate a scalable scheme for the simultaneous determination of internal and motional states in trapped ions with single-site resolution. The scheme is applied to the study of polaritonic excitations in the Jaynes-Cummings-Hubbard model with trapped ions, in which the internal and motional states of the ions are strongly correlated. We observe quantum phase crossovers of polaritonic excitations in two ions by directly evaluating their variances per ion site. Our work establishes an essential technological method for large-scale quantum simulations of polaritonic systems. Quantum simulations allow us to study the properties of many-body quantum systems that are hard to investigate with classical computers. A promising platform for realizing quantum simulations is a system of trapped ions. Trapped ions have advantages over other systems from such perspectives as ease of preparation and control, and we can address individual particles with little perturbation to neighboring particles. TheJaynes-Cummings (JC) model describes the atom-field interaction in a combined system of a two-level atom and a quantized electric-field mode. An interconnected array of two-level atoms interacting with quantized wave modes is known as the Jaynes-Cummings-Hubbard (JCH) model, and related systems of coupled cavity arrays have been extensively investigated. The JCH model can be realized with arrays of cavity QED systems and of circuit QED systems, as well as systems of trapped ions. These systems can be flexibly controlled with sets of system parameters.Therefore, they can be considered to be attractive systems for studying quantum many-body phenomena. In the JCH model, quasiparticles called polaritons play an essential role. Each polariton is represented as the superposition of an internal excitation and a photon or a motional excitation (phonon). Polaritons are well-defined particles in the JCH model and their total number is conserved.
The implications for understanding the JCH model are apparent in the quantum phase transition of a JCH system between the Mott -insulator (MI) and superfluid (SF) phases, which are characterized by a drastic change in the polariton-number variance per site.
In conclusion, we proposed a scalable scheme for the simultaneous determination of internal and motional states in trapped ions based on conditional measurements. The scheme was applied to a system of polaritons in the JCH model, and a phase crossover was studied by evaluating the quantities such as the variance for the total excitation number (polariton number) per site. The scheme proposed here can be applied to larger JCH systems where steeper phase crossovers and transitions as well as non-equilibriumbehaviors reflecting interactions are expected. In addition, the scheme can also be applied to other subjects in quantum simulations with trapped ions where both the internal and motional degrees of freedom are fully exploited as the simulation resources.

17:00 Evaporation and Large Arrays of Laser Cooled CaF Molecules

The wide-ranging scientific applications of ultracold molecules have inspired significant efforts in cooling and controlling molecules in the single quantum state level. Many potential applications are still hampered by the finite temperatures experimentally achieved. As temperatures are reduced further, motional decoherence rates are suppressed and fidelities increase, opening new opportunities for quantum simulations and computation. One of the most successful cooling methods for atomic species, evaporative cooling, requires a high elastic rate and large ratio of elastic to inelastic collisions. While this ratio is typically low for most molecules, using microwaves we engineer a repulsive barrier between molecules, shielding inelastic losses while increasing the rate of elastic collisions. Using optically trapped CaF molecules, we demonstrate that the elastic rate can be increased while the inelastic loss is suppressed to reach a ratio of 50. By adiabatically lowering the trap depth to force evaporate of the hottest molecules, we observed a drop in temperature of the sample when shielding was enabled compared to a control sample without shielding. Future improvements in initial density and number would allow for more effective evaporation. Evaporative cooling is useful for bulk samples, but to use molecules in single optical tweezer arrays requires single particle cooling. To this end we report progress towards sideband cooling of CaF molecules to the ground motional state of an optical tweezer.

17:00 Exploring sound excitations in 2D Bose gases

An interacting two-dimensional (2D) Bose gas becomes superfluid below a critical temperature through the BKT mechanism. In this phase, under hydrodynamic conditions where collisions keep the gas in local thermodynamic equilibrium, Landau's two-fluid model predicts the existence of two distinct sound-like excitations. These, so-called first and second sounds, have recently been observed in 2D [1], verifying the validity of the two-fluid model for a 2D superfluid. In the opposite limit of infrequent collisions, a distinct sound wave originating from the mean-field interactions of the quasicondensate is predicted to prevail even in the absence of the superfluid [2]; this ‘collisionless’ sound has also been observed in experiments [3].

Here, aiming to bridge the gap between the above observations, we extend our previous measurements [1] to explore the sound excitations of the interacting 2D $^{39}$K Bose gas throughout the crossover between the hydrodynamic and the collisionless limits. To control the nature of the induced sound waves, we vary the wavelength of sound excitations by directly exciting higher-wavevector modes using a digital micromirror device (DMD). This allows us to study the crossover from hydrodynamic to collisionless sound under the same conditions of the gas, including the different damping mechanisms of these sound modes. Moreover, we also probe sound waves at various temperatures, to connect the hydrodynamic sound modes with the well-known zero-temperature (collisionless) Bogoliubov excitations.

[1] Christodoulou, Panagiotis, et al. "Observation of first and second sound in a BKT superfluid." Nature 594.7862 (2021): 191-194.

[2] Ota, Miki, et al. "Collisionless sound in a uniform two-dimensional Bose gas." Physical Review Letters 121.14 (2018): 145302.

[3] Ville, J. L., et al. "Sound propagation in a uniform superfluid two-dimensional Bose gas." Physical Review Letters 121.14 (2018): 145301.

17:00 Exploring the supersolid stripe phase in a spin-orbit coupled gas with unequal interactions

Initially considered in the context of solid helium, the exotic supersolid phase is characterized by the spontaneous breaking of gauge and spatial translation symmetries. This implies acquiring the phase coherence of a superfluid and the crystalline structure of a solid. The long-sought regime has been recently observed for cavity-coupled atomic systems [1], dipolar gases [2-4] and spin-orbit coupled [5,6] (SOC) systems. Although evidence of supersolidity was shown for the latter, further exploration is hindered by the low contrast of the density modulation and its fragility.

Here, we present theoretical and experimental results on the exploration of the supersolid phase in a $^{39}$K spin-orbit coupled Bose Einstein condensate. We show that the stripe phase becomes more stable than in state-of-the-art experiments in rubidium. The reason is that the atomic interactions of the two-component condensate can be modified to be weakly attractive (miscible), favouring the striped regime. Thanks to the high contrast of the density modulation, the supersolid phase has a peculiar excitation spectrum manifested in the strong modification of the collective modes [7], which we numerically investigate for realistic parameters. Moreover, we present our experimental strategy to directly observe the density modulation of the supersolid in our system by increasing the imaging resolution using matter-wave lensing. This work aims to explore the differences and similarities between the SOC supersolid and realizations in other systems, highlighting the inherent features of a supersolid and the characteristics of each system.

[1] J. Léonard, et al., Nature 543, 87 (2017)
[2] L. Tanzi, et al., Phys. Rev. Lett. 122 130405 (2019)
[3] F. Böttcher, et al., Phys. Rev. X 9 011051 (2019)
[4] L. Chomaz et al., Phys. Rev. X 9 021012 (2019)
[5] J. R. Li, et al., Nature, 543, 91 (2017)
[6] A. Putra, et al., Phys. Rev. Lett., 124, 053605 (2020)
[7] K. T. Geier, et al., Phys. Rev. Lett. 127, 115301 (2021)

17:00 Faraday waves in strongly interacting superfluids

The study of collective excitations in superfluids systems has been an active and important research topic since the very beginning of the exploration of quantum fluids. Their study offers the possibility of probing several important properties of these systems, such as the spectrum of excitations, or the equation of state.

Here we present our work on the observation and study of Faraday waves in a cigar-shaped Fermi superfluid composed by a two-component spin mixture of $^6$Li atoms. These waves are a type of collective excitation that arises as a periodic spatial and temporal modulation of the gas density profile.

In our setup, Faraday waves are parametrically excited by modulating the radial frequency of the trap. We characterize the phenomenon as a function of the interaction parameter by means of a Feshbach resonance. We probe the superfluid excitation spectrum by extracting an effective 1D speed of sound for different values of the interaction parameter, in good agreement with numerical simulations. Finally, we perform a stability analysis in the parameter space using a simplified model and we show the emergence of the Faraday waves as unstable solutions to a Mathieu-like equation

17:00 FermiQP: A Fermion Quantum Processor

The most challenging problems from materials science and quantum chemistry involve strongly correlated states of mobile fermions. Mapping such itinerant systems to effective spin-1/2 systems realized on most quantum computing prototypes comes with a large computational overhead. New types of quantum processors based on inherently fermionic computation are therefore needed.

FermiQP will deliver a quantum processor based on ultracold fermionic Lithium operable in two modes. The analogue quantum gas microscopy mode will be using the fermionic nature of Lithium 6 to perform large-scale simulations of the Fermi-Hubbard model. The digital mode will enable quantum computation using spins manipulated by laser-driven single-qubit and superlattice-based global two-qubit gates allowing for universal programming. The device will thus enable new hybrid quantum computation schemes, where digital gate sequences are used for the initialization and readout of inherently fermionic analog quantum simulations. I will present the plans for and the current status of the FermiQP demonstrator.

17:00 Feshbach-enhanced odd- and even-wave interactions between identical fermions in quasi-one-dimensional confinement

Spin-polarized Fermi gases in low dimensions offer a pathway to the quantum simulation of matter. Through a Feshbach mechanism the p-wave ($L=1$) interactions governing these systems, which are suppressed by a centrifugal barrier at low energy, may be tuned and enhanced by a magnetic field. In doing so one may realize phenomena as diverse as chiral superfluidity in two dimensions to topological qubits in the form of Majorana fermions in a Kitaev chain in one dimension. We study the short-range correlations between atoms in an ensemble of quasi-one-dimensional (quasi-1D) tubes of fermionic potassium realized with a two-dimensional optical lattice. The p-wave contact in 1D is measured for the first time through few-body correlations that manifest in the high-momentum tail of radio-frequency spectroscopy. By varying magnetic field and lattice depth we observe that the odd-wave resonance is shifted by confinement, energetically narrow, and limited from reaching unitarity by loss. In a greater field range, we observe additional features due to orbital singlet collisional states facilitated by population in transverse excited bands. Such states are exchange anti-symmetric in the transverse confinement direction, resulting in axial even-wave character that exhibits broad energetic width and orders of magnitude larger correlation strength than the odd-wave case. These emergent even-wave collisions open new possibilities for strongly interacting p-wave systems and quantum simulation in low dimensions.

17:00 Heat rectification in ion crystals

Heat rectification, firstly observed in 1936 by Starr [1], is the physical phenomenon, analogous to electrical current rectification in diodes, in which heat current through a device or medium is not symmetric with respect to the exchange of the baths at the boundaries. In the limiting case the device allows heat to propagate in one direction from the hot to the cold bath while it behaves as a thermal insulator in the opposite direction when the baths are exchanged. In 2002 a paper by Terraneo [2] demonstrated heat rectification numerically for a chain of nonlinear oscillators in contact with two thermal baths at different temperatures. Since then, there has been a growing interest in heat rectification [3,4], and the field remains very active because of the potential applications in fundamental science and technology, and the fact that none of the proposals so far appears to be efficient and robust for practical purposes.

In this work, we study heat rectification in linear chains of ions in trap lattices with graded trapping frequencies, in contact with thermal baths implemented by optical molasses. To calculate the local temperatures and heat currents we find the stationary state by solving a system of algebraic equations [5]. This approach is much faster than the usual method that integrates the dynamical equations of the system and averages over noise realizations. We also show that even though, in early times, some kind of anharmonicity, i.e. non-linear forces, in the substrate potential or in the particle-particle interactions, was identified as a fundamental requisite for rectification, we show that asymmetric heat transport is found in this linear system if both the bath temperatures and the temperature dependent bath-system couplings are also exchanged. We can also show that it is the match/mismatch of the phonon bands (power spectra) the mechanism that governs the heat transport in the chain, allowing it when the bands match or obstructing it if they mismatch [6].

[1] C. Starr, Physics 7, 15 (1936).
[2] M. Terraneo, M. Peyrard, and G. Casati, Phys. Rev. Lett. 88, 094302 (2002).
[3] E. Pereira, EPL (Europhysics Letters) 126, 14001 (2019).
[4] N. Li, J. Ren, L. Wang, G. Zhang, P. Hänggi, and B. Li, Rev. Mod. Phys. 84, 1045 (2012).
[5] M. A. Simón, S. Martínez-Garaot, M. Pons, and J. G. Muga, Phys. Rev. E 100, 032109 (2019).
[6] M. A. Simón, A. Alaña, M. Pons, A. Ruiz-García, and J. G. Muga, Phys. Rev. E 103, 012134 (2021).

17:00 How much time do resonant photons spend as atomic excitations before being transmitted?

When a single photon traverses a cloud of 2-level atoms on resonance, how much time does it spend as an atomic excitation, as measured by weakly probing the atoms? It turns out that the answer, on average, is simply the spontaneous lifetime, multiplied by the probability of the photon being scattered into a side mode. It is tempting to infer from this that photons that are scattered spend, on average, one spontaneous lifetime as an atomic excitation, and photons that are transmitted through the cloud spend no time at all as an atomic excitation. Our recent experimental work [PRX Quantum 3, 010314] shows that this inference is incorrect, and that transmitted photons do spend time as atomic excitations. However, a complete theoretical treatment of the open-system dynamics for such a system has never, to our knowledge, been carried out. We examine this problem using the weak-value formalism, and find that the time that a transmitted photon spends as an atomic excitation is equal to the group delay experienced by the photon. Surprisingly, this equivalence remains true even for resonant, narrowband photons, for which the group delay is negative. We also determine the corresponding time for scattered photons, which turns out to be related to the "Wigner time" associated with elastic scattering. This work provides insight into the complex histories of photons travelling through absorptive media.

17:00 Improvements on direct-bonded copper, atom chips used for Cold-Atom Atomic Interferometry.

The Air Force Research Laboratory (AFRL) has been developing atom chips for use with cold-atom sensing and atom interferometry. We detail numerous advances in processing and fabrication techniques. Design improvements support tighter traps and rapid prototyping. Development of vias allow atom chips to serve as vacuum-chamber walls, decreasing current demands. Fabrication innovations that improve planarization support the integration of micro-features on single chips and chip-based assemblies.

17:00 Light-induced correlations in cold dysprosium atoms

With the evergrowing interest in quantum cooperativity, comes an ongoing
effort to study light-induced correlations in atomic media. In
these typically extreme dense regimes, with atomic distances below
the scattering lights wavelength, a direct matter-matter coupling is introduced
by electric and magnetic interactions. We intend to study
light-matter interactions in dense dipolar media with large magnetic
moments to explore the impact of magnetic dipole-dipole interactions
onto the cooperative response of the sample. With the largest groundstate
magnetic moment in the periodic table (10 Bohr-magneton), Dysprosium
is the perfect choice for these experiments.
This poster reports on our recent work to generate dense ultracold
dysprosium clouds utilizing a microscopic optical dipole trap. Further,
we give a perspective on future adaptations of this technique with a
self-built science cell, that serves as a highly accessible platform to
manipulate the atomic cloud. The small dimensions of the cell allow
for extremely tight optical dipole trapping and precise magnetic field
control at the position of the atoms.

17:00 Long-lived phantom helix states in Heisenberg quantum magnets

Exact solutions for quantum many-body systems are rare, but provide valuable insights for the description of universal phenomena. Recently, specific solutions of the Bethe ansatz equations for 1D anisotropic Heisenberg m​​odels were found that can carry macroscopic momentum yet no energy on top of the ferromagnetically ordered "vacuum" state, dubbed phantom Bethe states. As a consequence of these phantom Bethe states, simple spin helix states at special wave-vector becomes exact eigenstates of these systems.

With ultracold Li-7 atoms on optical lattices, we can simulate the anisotropic Heisenberg model, and tune the interaction anisotropy with Feshbach resonance. Here, we show experimentally that there exist special helical spin patterns in 1D chains which are long-lived, relaxing only very slowly in dynamics. The wave-vector of these special helices also shifts with the anisotropy parameter. These results confirming theoretical predictions.

As the wave-vector of the spin helix is determined by the anisotropy parameter, we use these phantom spin helices to directly measure the interaction anisotropy at different magnetic fields around Feshbach resonances. The measured anisotropy agrees well with the predictions based on super-exchange and Bose Hubbard model with perturbative interaction far from the Feshbach resonance, but we found discrepancies very close to the Feshbach resonance. This demonstrated the importance of higher order processes like bond charge tunneling close to the resonance, and reveals other processes not considered before (presented in detail in a separate poster).

We also generalize the theoretical description to higher dimensions and other non-integrable systems, and find analogous stable spin helices, which should show non-thermalizing dynamics associated with so-called quantum many-body scars. These results have implications for the quantum simulation of spin physics, as well as many-body dynamics.

17:00 Machine learning classification of two-dimensional vortex configurations.

We consider computer generated configurations of quantized vortices in planar superfluid Bose–Einstein condensates. We show that unsupervised machine learning technology can successfully be used for classifying such vortex configurations to identify prominent vortex phases of matter [1]. The machine learning approach could thus be applied for automatically classifying large data sets of vortex on figurations obtainable by experiments on two-dimensional quantum turbulence.

[1] R. Sharma and T.P. Simula, Machine-learning classification of two-dimensional
vortex configurations, Physical Review A, 105, 033301 (2022).

17:00 Mutual friction and diffusion of two-dimensional quantum vortices

We present a microscopic theory of thermally-damped vortex motion in oblate atomic superfluids that accounts for previously neglected number-conserving interactions between superfluid and thermal atoms. This mechanism causes dissipation of vortex energy due to mutual friction, as well as Brownian motion of vortices due to thermal fluctuations. We present an analytic expression for the dimensionless mutual friction coefficient that gives excellent quantitative agreement with experimentally measured values, without any fitted parameters. Our work provides a microscopic origin for the damping and Brownian motion of quantized vortices in two-dimensional atomic superfluids, which has previously been limited to phenomenology.

17:00 Negative absolute temperature state in a triangular optical lattice

Negative absolute temperature entails a situation where the entropy of a system reduces as the internal energy increases. As the idea was put forward by N. Ramsey in the 1950s [1], the concept of negative absolute temperature has been actively discussed, and has led to the eventual observation with cold atoms in a square lattice [2]. In this poster, we describe our experiment with K(39) atoms on the observation of negative absolute temperature in a triangular optical lattice — a non-bipartite lattice containing geometric frustration. Due to its non-bipartite nature, the lowest energy band of a triangular lattice hosts two non-equivalent highest-energy points ($K$ and $K'$ points in Fig. 1(a)) that are not connected via a reciprocal lattice vector. We study the influence of these non-equivalent points by comparing positive and negative temperature states in this lattice. In Fig. 1(b), atoms in negative absolute temperature state are shown in the superfluid state where the atoms occupy the two highest energy points equally.

Figure 1: (a) The band structure of the first band for a triangular optical lattice. The inequivalent energy maxima are located at the $K$ and $K'$ points while the minimum of the energy is at the $\Gamma$ point. (b) The measured optical density after an 11 ms time-of-flight, of a negative temperature gas. The region enclosed by the black thin lines represents the first Brillouin zone.

Moreover, we have created a phase-stabilized optical Kagome lattice by superimposing a 532-nm triangular lattice and a 1064-nm honeycomb lattice. We have also observed the superfluid to Mott insulator transition in the Kagome lattice.

References:
[1] N.F. Ramsey “Thermodynamics and statistical mechanics at negative absolute Temperatures” Phys. Rev. 103, 20 (1956).
[2] S. Braun, J.P. Ronzheimer, M. Schreiber, S.S. Hodgman, T. Rom, I. Bloch, and U. Schneider “Negative absolute temperature for motional degrees of freedom” Science 339, 53 (2013).

17:00 Nuclear T-violation search using octupolar nuclei in a crystal

The matter-antimatter asymmetry of the universe suggests that new sources of time-reversal symmetry (T) violation lurk at energy scales beyond the reach of colliders. New particles or T-violating interactions coupled to nucleons can lead to nuclear Schiff moments or magnetic quadrupole moments, which result in measurable energy differences between the spin states of nuclei inside electrically polarized atoms.

Nuclei with the highest intrinsic sensitivity to T-violation (octupolar nuclei) are often short-lived radioactive isotopes. Further, obtaining large atomic polarization typically requires the use of heavy polar molecules that are challenging to cool and trap. Therefore, demanding both enhancement factors -- large intrinsic T-violation sensitivity and large atomic polarization -- usually leads to significant experimental complexity and limited choices for feasible nuclear/molecular candidates. We present a way to evade these constraints and access both the enhancement factors using stable nuclei in a solid.

Our approach uses $^{153}$Eu doped into a crystal, which realizes a large ensemble of octupolar nuclei within strongly polarized atomic ions. This system offers a simple but powerful means to hunt for T-violating physics at PeV-scale energies. We will discuss the details of our approach and our progress towards a pathfinder experiment.

17:00 Observation of a molecular bond between ions and Rydberg atoms using a high-resolution pulsed ion microscope

We present our recent studies on Rydberg atom-Ion interactions and the spatial imaging of a novel type of molecular ion using a high-resolution ion microscope. The ion microscope provides an exceptional spatial and temporal resolution on a single atom level, where a highly tuneable magnification ranging from 200 to over 1500, a resolution better than 200nm and a depth of field of more than 70µm were demonstrated [1]. A pulsed operation mode of the microscope combined with the excellent electric field compensation enables the study of highly excited Rydberg atoms and ion-Rydberg atom hybrid systems.
Using the ion microscope, we observed a novel molecular ion, where the bonding mechanism is based on the interaction between the ionic charge and an induced flipping dipole of a Rydberg atom [2]. Furthermore, we could measure the vibrational spectrum and spatially resolve the bond length and the angular alignment of the molecule. The excellent time resolution of the microscope enables probing of the interaction dynamics between the Rydberg atom and the ion.

[1] C. Veit, N. Zuber, O. A. Herrera-Sancho, V. S. V. Anasuri, T. Schmid, F. Meinert, R. Löw, and T. Pfau, Pulsed Ion Microscope to Probe Quantum Gases, Phys. Rev. X 11, 011036 (2021).
[2] N. Zuber, V. S. V. Anasuri, M. Berngruber, Y.-Q. Zou, F. Meinert, R. Löw, T. Pfau, Spatial imaging of a novel type of molecular ions, Nature 5, 453 (2022)

17:00 Observation of Cooper Pairs in a Mesoscopic 2D Fermi Gas

Pairing is the fundamental requirement for fermionic superfluidity and superconductivity. To understand the mechanism behind pair formation is an ongoing challenge in the study of many strongly correlated fermionic systems.
On this poster, I present the direct observation of Cooper pairs in our experiment. We have implemented a fluorescence imaging technique that allows us to extract the full in-situ momentum distribution with single particle and spin resolution. We apply it to a mesoscopic Fermi gas, prepared deterministically in the ground state of a two-dimensional harmonic oscillator. Our ultracold gas allows us to tune freely between a completely non-interacting unpaired system and weak attractions where we find Cooper pair correlations at the Fermi surface. When increasing the interactions even further, the pair character is modified and the pairs gradually turn into tightly bound dimers. The collective behavior that we discover in our mesoscopic system is closely related to observations in nuclear physics or metallic grains. Our method provides a new pathway to study many of the outstanding questions concerning fermionic pairing, for example in imbalanced systems or the normal phase.

17:00 On-chip trapped cold atom interferometer with spatial splitting

Since the 90's, many laboratories have developed atom interferometers to sense accelerations and rotations [1]. For many applications, small compact devices are desirable, and the atom chip [2] appears to offer a path towards miniaturization. Moreover, performing the interferometry sequence on-chip with trapped atoms decouples the sensitivity of the sensor from its size, allowing in principle, larger interrogation times while shrinking the device's size. It has been shown that accelerations can be sensed from a Ramsey's interferometer by spatially splitting the two states of the atoms during the interrogation time [3]. This can be done by separating the two states, using state selective, near-field microwave gradients from a coplanar waveguide [4,5].

We have recently demonstrated state-selective displacements of a two component thermal cloud using coplanar waveguides. The separation of the internal states is several microns and we have observed interference fringes upon recombination showing that the separation was coherent. We have also studied the fringe contrast as a function of cloud temperature.

[1] Riehle et al., Phys. Rev. Lett. 67, 177 (1991)
[2] Reichel et al., Phys. Rev. Lett. 83, 3398 (1999)
[3] Dupont-Nivet et al., New J. Phys. 18 113012 (2016)
[4] Ammar et al., Phys. Rev. A, 91:053623 (2015)
[5] Böhi et al., Appl. Phys. Lett. 97, 051101 (2010)

17:00 Pathway to magneto-optical trapping of SrOH to probe for Dark Matter and EDMs

The complex structure of polyatomic molecules offers powerful features that can be exploited for applications in quantum simulation and precision measurement. One of these features is a plethora of ro-vibrational states. In the linear triatomic molecule SrOH, two vibrational states have a near-degeneracy that can be probed with microwaves (in contrast to typical vibrational splittings of $\sim$10 THz). Because the energies of these states depend differently on the proton-to-electron mass ratio, $\mu$, a microwave resonance between them is highly sensitive to changes in $\mu$ over time. We report on high-resolution vibrational branching ratio measurements of four excited vibronic states. We are now able to design a laser-cooling scheme with over 10,000 photon scatters before loss to an unaddressed vibrational state, more than enough to form a MOT and load an optical trap. Only 8 lasers are required for this scheme, fewer than for any other known polyatomic molecule cooling cycle. We describe progress towards laser cooling of SrOH and a high-sensitivity measurement of $\mu$ variation using ultracold SrOH molecules.

17:00 Photoassociation Specroscopy of RbYb near the Yb intercombination lie

Ultracold dipolar molecules are a promising system for interesting research in ultracold chemistry, novel interactions in quantum gases, precision measurements or quantum information.

Here we report on photoassociation spectroscpoy in an ultracold mixture of Yb and Rb near the $^1S_0 \rightarrow {}^3P_1$ intercombination line of Yb at 556 nm. While in previous work we have identified several one- and two-photon photoassociation transitions near the D1-line of Rb at 795 nm [1,2], photoassociation near the narrow intercombination line promises to open up new pathways for the production of YbRb-molecules in the absolute molecular ground state.

The experiments presented here, have been carried out in a completely new setup which is designed to spatially separate the production of ultracold atomic samples from the actual experimental studies [3]. In this setup we employ optical tweezers to transport individually cooled samples of ultracold Rb and Yb atoms from their separate production chambers to a dedicated common science chamber. In the science chamber the atoms can be further manipulated and trapped using various optical dipole trap geometries.

So far, we have experimentally observed one unbound-bound transition in a mixture of $^{170}$Yb and $^{87}$Rb near the intercombination line. We attribute the fact that no more transitions could be detected to the fact that the unbound-bound transition matrix elements are significantly smaller than expected. Using the observed excited RbYb* molecular level as an intermediate state we could also identify two two-photon transitions to vibrationally excited levels in the electronic ground state of the molecule using a dark-resonance technique. We plan to use the dark-resonances to identify deeply bound rovibrational levels in the electonically excited $1^2\Pi_{1/2}$ molecular state, which are suitable for an efficient transfer of the RbYb molecules into the absolute ground state.

[1] M. Borkowski et al., PRA 88, 052708 (2013)
[2] C. Bruni et al., PRA 94, 022503 (2016)
[3] C. Sillus et al. Rev. Sci. Inst. 92, 033204 (2021)

17:00 Polyatomic ultralong range Rydberg molecules

In cold and ultracold mixtures of atoms and molecules, Rydberg interactions with surrounding atoms or molecules may, under certain conditions, lead to the formation of special long-range Rydberg molecules [1, 2, 3]. These exotic molecules provide an excellent toolkit for manipulation and control of interatomicand atom-molecule interactions, with applications in ultracold chemistry, quantum information processing and many-body quantum physics. In this poster, we discuss ultralong-range polyatomic Rydberg molecules formed when a heteronuclear diatomic molecule is bound to a Rydberg atom [3, 4]. The binding mechanism appears due to anisotropic scattering of the Rydberg electron from the permanent electric dipole moment of the polar molecule. We propose an experimentally realizable scheme to produce these triatomic ultralong-range Rydberg molecules in ultracold RbCs traps, which might use the excitation of cesium or rubidium [5]. By exploiting the Rydberg electron-molecule anisotropic dipole interaction, we induce a near resonant coupling of the non-zero quantum defect Rydberg levels with the RbCs molecule in an excited rotational level. This coupling enhances the binding of the triatomic ultralong-range Rydberg molecule and produces favorable Franck-Condon factors.

Another type of ultralong-range Rydberg molecule is formed in collisions between polar molecules in cold and ultracold settings [6]. The interaction of  -doublet nitric oxide (NO) with long-lived Rydberg NO molecules forms ultralong-range Rydberg bimolecules with GHz energies and kilo-Debye permanent electric dipole moments. The description includes both the anisotropic charge-molecular dipole interaction and the electron-NO scattering. The rotational constant for the Rydberg bimolecules is in the MHz range, allowing for microwave spectroscopy of rotational transitions in Rydberg bimolecules. The Rydberg molecules described here hold promise for studies of a special class of long-range bimolecular interactions.

[1] C. H. Greene, A. S. Dickinson, and H. R. Sadeghpour, Phys. Rev. Lett. 85, 2458 (2000).
[2] S. T. Rittenhouse and H. R. Sadeghpour, Phys. Rev. Lett. 104, 243002 (2010).
[3] V. Bendkowsky, et al , Nature 458, 1005 (2009).
[4] R. Gonzaalez-Ferez, H. R. Sadeghpour, and P. Schmelcher, New J. Phys. 17, 013021 (2015).
[5] R. Gonzalez-Ferez, et al, J. Phys. B 53, 074002
(2020).
[6] R. Gonzalez-Ferez, J. Shertzer and H. R. Sadeghpour Phys. Rev. Lett. 126, 043401 (2021).

17:00 Probing Hubble Attenuation and Amplification in a Expanding and Contracting Bose Einstein Condensate

In cosmology, the relativistic scalar fields that cause the universe to expand are damped by Hubble friction, which is due to the dilation of the underlying spacetime metric. Here, we have simulated the Hubble friction using a toroidal Bose-Einstein condensate (BEC) of 23Na atoms, in which the phonon fields can serve as an analogy to the cosmological scalar fields. We experimentally measure both Hubble attenuation and amplification, with five-fold better accuracy, by expanding and contracting the BEC universe. We discover temporal phase-dependent attenuation and amplification of the phonon field, which is only possible under non-adiabatic processes and is not described by the theoretical model. The measured strength of the Hubble friction disagrees with recent theories.

17:00 Programmable Interactions and Emergent Geometry in a 1D Array of Atomic Ensembles

Control over the structure of interactions is essential for developing flexible quantum protocols. We couple an array of atomic ensembles to a driven optical cavity, creating an XY model. Using a magnetic field gradient and modulating the cavity field enables us to prune the naturally all-to-all connectivity of cavity-mediated interactions. We confirm these coupling graphs by direct measurements of two-point correlation functions. From the correlation measurements, we infer the structure and Euclidean embedding of the equivalent Hamiltonian with only local interactions. Example geometries include a Moebius ladder and a cylinder with sign-changing interactions.

This control of interactions can be leveraged to study a wide range of physical systems, including quantum gravity and quantum computation. We simulate spin systems relating quantum mechanics and gravity, inspired by a discretized formulation of the AdS/CFT correspondence. We show that the states generated by the cavity dynamics map to low-energy states of the programmed XY model. Finding the ground state of the XY Hamiltonian is an NP-hard problem, and these highly-programmable interactions open avenues towards spin-glass physics and physically-encoded computation.

17:00 Progress towards a magneto-optical trap for MgF molecules

Achieving ultracold temperature of neutral diatomic molecules is one of the pre-requested key steps for using them as a quantum platform. Owing to molecules' abundant internal structures and large electric dipole moments, a long coherence time and a long-range interaction could be achieved when we make an array of diatomic molecules trapped in optical tweezers.
To make an ultracold molecular array, several steps are planned in this research. First, a cold buffer-gas beam of molecules is generated by elastic collisions with He buffer gas after the ablation of a molecule target. Second, the molecular beam is captured in a magneto-optical trap, cooling the molecules down to the Doppler-limit regime. The last step is sub-Doppler cooling and transferring the molecules into optical dipole traps to construct an ultracold molecular array.
MgF molecules are chosen here because of their favorable energy structure for laser cooling and abundant bosonic and fermionic isotopes. We constructed a buffer-gas beam source that can generate MgF molecules and cool them down below 4 K. At this temperature, 30 % of the molecules are in the $ v=0, N=1$ state, which is the electronic ground state of the quasi-cycling transition for the magneto-optical trap. The poster will provide detailed information about the overall experiment and the performance of the buffer-gas beam source.

17:00 Prospects for Constraints on Nanometer-Range Non-Newtonian Gravity with a State-of-the-art Molecular Clock

Ultracold molecules are a powerful platform for metrology, precision measurements and searches for new, beyond-the-Standard-Model physics. In particular, Sr$_2$, thanks to its simple structure, insensitivity to external fields and narrow optical transitions, provides an excellent testbed for the search for new interactions. Here, we present a detailed characterisation of our $^{88}$Sr$_2$ molecular clock for a vibrational transition spanning the entire depth of the ground state potential. We control systematic shifts at the $10^{-14}$ level and perform absolute frequency measurements at the $10^{-13}$ level, limited by GPS-based time transfer infrastructure. We discuss prospects to use strontium isotopologues to place improved constraints on new mass-dependent forces, including possible pathways toward the production of ultracold $^{86}$Sr$_2$ and $^{84}$Sr$_2$ dimers and spectroscopy of clock lines in these species.

17:00 Quantum caustics in many-body dynamics

Caustics are singularities arising from natural focusing and are well known in optics but also occur in any system that has waves including quantum waves. Caustics take on universal shapes that are described by catastrophe theory and dominate interference patterns in the semiclassical regime.
My group has been extending these ideas to quantum fields, such as those found in the sine-Gordon and Bose-Hubbard models. Our physical motivation is to describe the dynamics of Bose-Einstein condensates (BECs) following a sudden quench, including the cases of two and three independent BECs that are suddenly coupled together.

Our theoretical simulations [1] of the dynamics of these low-dimensional many-body systems following the quench shows that caustics form in Fock space over time and this seems to be a generic phenomenon. Furthermore, the caustics are singular in the mean-field theory but are regulated and adopt universal interference patterns in the full many-body theory. These caustics represent a form of universal quantum many-body dynamics associated with singularities in the underlying classical dynamics.

[1] Caustics in quantum many-body dynamics, W. Kirkby, Y. Yee, K. Shi and D.H.J. O’Dell, Phys. Rev. Research 4, 013105 (2022).

17:00 Quantum nonlinear optics in atomic dual arrays

Sub-wavelength arrays of atoms have been shown to have remarkable optical properties, like near perfect reflection and low diffraction loss. However, the collective effects resulting in these properties also serve to wash out the otherwise strong underlying nonlinearity of the atoms, rendering the arrays largely linear. We have found that by putting together two arrays we can recover a strong nonlinearity via an emergent cavity-like behaviour with a large delay time that allows photons to interact strongly before being emitted from the system. Such a quantum metasurface opens up new possibilities for manipulating non-classical light, from implementing quantum information operations to simulating many-body physics with interacting photons.

17:00 Quantum Optimization of Maximum Independent Set using Rydberg Atom Arrays

Realizing quantum speedup for solving practically relevant, computationally hard problems is a central challenge in quantum information science. Using Rydberg atom arrays composed of up to 289 coupled qubits in two spatial dimensions, we experimentally investigate quantum optimization algorithms for solving the Maximum Independent Set problem. We use a hardware-efficient encoding associated with Rydberg blockade, realize closed-loop optimization to test several variational algorithms, and subsequently apply them to systematically explore a class of nonplanar graphs with programmable connectivity. We find that the problem's hardness is controlled by the solution degeneracy and the number of local minima, and experimentally benchmark the quantum algorithm's performance against optimized classical simulated annealing. On the hardest instances, we observe a superlinear quantum speedup in finding exact solutions for sufficiently long evolution times beyond the shallow-circuit-depth regime, and analyze its origins.

17:00 Quasi-BIC mode lasing in a quadrumer plasmonic lattice

Plasmonic lattices of metal nanoparticles have emerged as an effective platform for strong light-matter coupling, lasing, and Bose-Einstein condensation. However, the full potential of complex unit cell structures has not been ex- ploited. On the other hand, bound states in continuum (BICs) have attracted attention, as they provide topologically protected optical modes with diverging quality factors. Here, we show that quadrumer nanoparticle lattices enable lasing in a quasi-BIC mode with a highly out-of-plane character. By combining theory with polarization-resolved measurements of the emission, we show that the lasing mode has a topological charge. Our analysis reveals that the mode is primarily polarized out-of-plane as a result of the quadrumer structure. The quality factors of the out-of-plane BIC modes of the quadrumer array can be exceedingly high. Our results unveil the power of complex multi-particle unit cells in creating topologically protected high-Q modes in periodic nanostructures.

Speaker: Grazia Salerno (Aalto University)

17:00 Quasi-continuous superradiance on the kHz clock transition of 88Sr

Lasing in the superradiant or “bad cavity” regime has attracted interest in the optical clock community as it offers an alternative to conventional lasers limited by the thermal noise fluctuations of reference cavities. In our experiment, we investigate pulsed lasing on the 7.5 kHz clock transition of $^{88}$Sr atoms in an optical cavity. We continuously repump the lasing to achieve pulse durations on the ms scale, compared to a pulse length of a few $\mu$s using a single population inversion pulse. To observe the narrowing of the spectral line, we constructed an ultra-stable reference cavity system in order to characterize the spectral properties of the emission. Lastly, we experimentally investigate the prospect of using superradiant pulses as a readout of a Ramsey interferometer sequence. This scheme has the advantage of a fast, non-destructive measurement with increased sensitivity, which would be beneficial to the performance of optical atomic clocks.

17:00 Realization of dipolar XY quantum ferro & antiferromagnets with arrays of Rydberg atoms.

In this poster we present the realization of ferromagnets (FM) and antiferromagnets (AFM) for square arrays up to 100 atoms realizing the dipolar XY model. Our platform is based on individual atoms of rubidium trapped in arrays of optical tweezers. We encode the effective spin on two Rydberg states. The coupling between the spins results from the resonant dipole-dipole interaction, varying as $1/r^3$. Our preparation of the phase relies on an adiabatic procedure starting from a classical anti-ferromagnetic state prepared by using local energy shifts which are induced by onsite addressing beams. The FM and AFM states are respectively the highest and the lowest energy state of the dipolar XY model.
To investigate these states, we first measure the dynamics of the magnetizations and the growth of correlations along different directions as we enter the FM (AFM) phase. We show that the two phases emerge for different critical values of the control parameters during the adiabatic procedure. This difference is explained by the weak frustration induced by the long-range tail of the dipolar interaction for the AFM case. Finally, by analyzing the spatial profile of the correlations we show the presence of a long-range order for the FM, feature that vanishes for the AFM, consistent with the existence of a weakly frustrated order.

17:00 Rydberg Atom Interactions with an Optical Nanofiber

Cold Rydberg atoms have recently become a promising platform for quantum information processing and quantum simulations due to their specific properties. The Rydberg blockade regime allows us to entangle qubits and to make CNOT and CPhase gates. Optical nanofibers (ONFs) are an excellent tool to interact with such atoms. They are relatively easy to install into experimental setups because of the simplicity of coupling light into and out of them. The evanescent field decaying from the nanofiber can excite the atoms from the ground state or produce a dipole trap to localize them around the nanofiber. A probe light sent through the fiber is sensitive to the presence of the atoms in the vicinity of the nanofiber and can be used to collect information from neutral atom qubits. To have a precise control over such a system one needs to know all the interactions happening between the atoms and the nanofiber material. We exploit a two-photon ladder-type excitation in $^{87}$Rb by using 780 nm magneto-optical trap (MOT) cooling lasers and 480 nm light coming from the evanescent field of an ONF. The 480 nm light is locked by an external vapor cell EIT to a particular Rydberg transition. During the experiment, the MOT is overlapped with the ONF region and, firstly, reaches an equilibrium atom population. Then, the 480 nm laser is turned on, and the atoms in the vicinity of the ONF undergo Rydberg excitation and get lost from the MOT. This process introduces an additional loss rate to the MOT population, which we measure by collecting the fluorescence signal. By scanning the 480 nm light across the transition we observe coherent and incoherent Rydberg excitation processes. The experiment was reproduced for excitation to nS$_{1/2}$, nD$_{3/2}$ and nD$_{5/2}$ Rydberg states for a wide range of principal quantum number, n, values.

17:00 Rydberg atoms in Bose-Einstein condensed environments: cold bubble chambers and mesoscopic entanglement

Rydberg Atoms in highly excited electronic states with n=30-200 can be excited within Bose-Einstein condensates (BECs), and while lifetimes are shorter than in vacuum [1,2], these atoms live long enough to cause a response of the BEC mean field [3]. During this, thousands of ground-state atoms are present within the Rydberg orbit, allowing the study of atoms moving within atoms [4].
We present beyond-mean field models of the joint Rydberg-BEC dynamics, showing how either can be used to probe the other.

For multiple Rydberg atoms in a single electronic state, we show that the phase coherence of the condensate allows the tracking of mobile Rydberg impurities akin to the function of bubble-chambers in particle physics [5]. For a single Rydberg atom with multiple electronic states, we provide spectral densities of the BEC as a decohering environment [6], and show that the BEC can image a signature of the entangling evolution that causes Rydberg q-bit decoherence [7] or serve as non-Markovian environment for quantum simulations.

[1] Schlagmüller et al. PRX 6 (2016) 031020.
[2] Kanungo et al. PRA 102 (2020) 063317.
[3] Balewski et al. Nature 502 (2013) 664.
[4] Tiwari et al. arXiv:2111.05031 (2021).
[5] Tiwari et al. PRA 99 (2019) 043616.
[6] Rammohan et al. PRA 103 (2021) 063307.
[7] Rammohan et al. PRA(Letters) 104 (2021) L060202.

Speaker: Dr Sebastian Wuster (Indian Institute of Science Education and Research Bhopal)

17:00 Scalable cryogenic experiment for trapped-ion quantum computing with long ion strings

We present experimental work performed in a cryogenic apparatus exploiting a segmented ion trap architecture for the implementation of quantum algorithms [1]. The quantum register consists of a linear string of 40Ca+ ions which are individually controlled by tightly focused laser beams perpendicular to the crystal axis. Light is delivered by a waveguide array allowing to individually feed each ion with a separately controlled laser beam.

High-fidelity gate operations require both a stable qubit system and precise control over optical fields. In order to control multiple ions in parallel, we have developed a scalable single ion addressing system based on an array of waveguides matched to the ion positions, making the optical addressing system compact and robust against mechanical noise. What is more, this single ion addressing capability will mitigate the need for ion transport operations and allow for parallel qubit manipulations thereby simplifying the overall computation. In order to improve qubit coherence times we have implemented a set of superconducting coils in a "self-shielding" configuration, which enables the suppression of magnetic field fluctuations at all frequencies down to DC [2]. Ion imaging is performed using a camera with low pixel count with state-detection via FPGA-based image processing. This should allow low-latency readout of many ions in parallel, which is essential for implementing fast feedback required for error-correction. Design considerations and experimental progress will be presented.

This work is supported by IARPA.

[1] Decaroli, C., Matt, R., Oswald, R., Axline, C., Ernzer, M., Flannery, J., Ragg, S. and Home, J.P., 2021. Design, fabrication and characterization of a micro-fabricated stacked-wafer segmented ion trap with two X-junctions. Quantum Science and Technology, 6(4), p.044001.

[2] Gabrielse, G. and Tan, J., 1988. Self‐shielding superconducting solenoid systems. Journal of Applied Physics, 63(10), pp.5143-5148.

17:00 Scale factor corrections for point-source atom interferometer gyroscopes

Point-source atom interferometry (PSI) offers a pathway for realizing compact inertial sensors with relatively low experimental complexity. Rotation sensing in PSI gyroscopes uses the velocity distribution in an expanding cold-atomic cloud to realize many parallel atom interferometers with velocity-dependent phase shifts. The scale factor relating the rotation rate to the observed atomic population fringes depends on the spatial distribution of atoms at the beginning of the atom interferometry sequence. For magneto-optical trap-based PSI gyroscopes, these size-dependent corrections to the scale factor are significant and scale factor errors contribute to both the accuracy and long-term stability of PSI-based rotation measurements. For Gaussian atomic density profiles, scale factors can be analytically corrected using the magnification ratio between initial and final gas sizes. Here, we present a method to correct scale factor for arbitrary initial cloud shapes and sizes, and we comment on the limitations to long-term gyroscope stability due to cloud size stability.

17:00 Shear interferometry in microgravity with atomic ensembles in the picokelvin regime

Atom interferometry as a tool for precision measurements opens up a broad field of application: from testing fundamental physics to geodesy or navigation. Since the sensitivity of an atom interferometer scales quadratically with the interrogation time, operating on a microgravity platform is highly beneficial. Extended times of flight of several seconds require low expansion rates of the atomic ensemble, which can be achieved with magnetic lensing, also known as delta-kick collimation. To pave the way for space-borne atom interferometry, the QUANTUS-2 experiment was developed. This high-flux rubidium BEC machine, based on the atom chip technology, is designed to operate at the 110m high ZARM drop tower in Bremen, Germany, where microgravity times of 9.7$\,$s can be reached.
In this contribution, a quadrupole-mode enhanced magnetic lens is presented to achieve a three-dimensional collimated BEC. The resulting atomic ensemble features an ultra-low internal 3D kinetic energy of $\frac{3}{2} k_B \cdot$ 38$\,$pK and a high signal to noise ratio even after 2$\,$s time of flight [1]. The novel application of a Ramsey sequence as a shear interferometer consisting of two successive double Bragg beam splitter pulses enables us to investigate the divergence of the BEC and possible magnetic lens imperfections. Additionally, the spatially resolved velocity spread can be deduced based on the recorded spatial interferometry pattern. The demonstrated atom interferometry with picokelvin ensembles provides the basis for future interferometry measurements on long time scales with the aim of unprecedented precision.
This project is supported by the German Space Agency DLR with funds provided by the Federal Ministry for Economic Affairs and Energy under grant number DLR 50WM1952-1957.

[1] C. Deppner, W. Herr, M. Cornelius, et al. "Collective-mode enhanced matter-wave optics." Physical Review Letters 127.10, 100401 (2021)

17:00 Study of radiative properties of helium isoelectronic sequence

The radiative properties of ions (Z= 2-53) belonging to the helium isoelectronic sequence are reported. Energy levels for the ground state and the lowest 1s2l singly excited states are considered. The effects of correlation effects are studied for the selected ions by increasing the active set (AS). Relativistic effects such as the Breit interaction and the QED corrections are also computed. The heavy elements with high Z are of potential interest in controlled thermonuclear fusion and astrophysics. Indeed, they could be used in plasma-facing materials such as the divertors in tokamaks or/and could be generated by neutron-induced transmutations of divertor’s materials. So, extensive spectroscopic studies both experimental and theoretical have been performed in the last years in order to estimate the power loss from the impurities in the forthcoming fusion reactors [1].
In this work, two independent theoretical atomic structure computational approaches have been considered, i.e. the ab initio multiconfiguration Dirac-Hartree-Fock with subsequent relativistic configuration interaction method (MCDHF-RCI) implemented in the code GRASP2018 [2] and the Dirac-Fock-Slater (DFS) implemented in the code FAC (Flexible Atomic Code) [3]. The relativistic configuration interaction method was applied to estimate the electron correlation effects. The transition probabilities and the oscillator strengths w calculated for E1, E2, M1 and M2 transitions spanning the spectral range from UV to IR. Our results are compared with available experimental and other theoretical values. Good agreement is found for the majority of cases. Lifetimes are also considered in this work, first to check the accuracy of calculated results of transitions rates and second, to complete the databases by a complete and accurate values of lifetimes. This can help future works by experimentalists to compare their results with those results calculated theoretically. Finally, this study underlines the importance of relativistic corrections especially for the heavy atomic ions. This computational approach enables us to present a consistent and improved data set of all important atomic data of the helium isoelectronic sequence, which are useful for identifying transition lines in further investigations.

References
[1] A. J. H. Donne et al., Nucl. Fusion 47 (2007) S337.
[2] C. Froese Fischer, G. Gaigalas, P. Jönsson, and J. Bieroń, Comput. Phys. Commun., 237 (2019) 184.
[3] M.F. Gu, Can. J. Phys. 86 (2008) 675-689.

17:00 Superradiance decoherence caused by long-range Rydberg-atom pair interactions

This work reports on the observation of superradiance decoherence caused by long-range dipole-dipole interactions between Rydberg atoms. A cold atom cloud is prepared in the mode volume of a weakly driven optical cavity, and excited to a Rydberg state. The cavity transmission monitors the Rydberg dynamics in real-time and detects superradiant enhancement of the transition rates between neighboring Rydberg states. The observed enhancement is reduced for increasing Rydberg atom density: a signature of atom pair-interactions. The observations are explained within a model based on the idea of Rydberg blockade reducing the atom number participating in the Dicke state, responsible for superradiance.

17:00 Suppression of Raman interaction due to destructive interference in alkali atoms

Raman interactions are a powerful tool for performing arbitrary rotations between two Zeeman levels of an individual ion or a neutral atom. Universality of the technique places it in a central role in many quantum technologies: single qubit gates in atomic quantum processors, mediating interactions in quantum simulators, and mapping quantum information into long-lived states in optical quantum memories, to name a few.

The conventional three-level effective theory manifests that the fidelity of the Raman operation grows inversely proportional to the single photon detuning. In our work we show that this approximation does not always hold for all alkali atoms due to their multi-level structure. The destructive interference of the hyperfine sub-levels could fully suppress the Raman interaction at large detunings leaving us with some finite optimal fidelity in comparison to asymptotically ideal theoretical case. We use a formalism based on Clebsch-Gordan coefficients and rotational symmetries of atoms, which allows us to generalize our results to all alkali atoms. We experimentally show the effect on Rb-87 and discuss how to circumvent the problem.

17:00 Toward A 1D Chain Of Cold Rydberg Atoms Next To An Optical Nanofiber

Combining cold Rydberg atoms with an optical nanofiber (ONF) apparatus provides a platform for both investigating the generation and manipulation of Rydberg atoms, but also an ideal way for generating a 1D chains of Rydberg atoms using the strong interactions of atom-ONF hybrid systems combined with the ability to trap atoms at the surface of the fiber in a 1D chain.

The evanescent field produced via the tight confinement of the light in an ONF allows for strong light-matter interactions for relatively low laser powers, and the easy interfacing with existing optical systems makes it an ideal system for the development of quantum technologies. Atom based ONF systems have shown great success in the field of atom optics, and with our recent success of exciting atoms to the Rydberg state via the evanescent field of the fiber! [1], are now a potential new platform for developing Rydberg based quantum information systems.
Rydberg atoms, with their large electric field sensitivity and strong inter-atomic interactions leading to the famed Rydberg blockade, are a strong candidate for quantum information systems and have been a topic of significant interest over the past years.
ONF systems have been used to trap atoms at the surface of the fiber using two-color dipole traps, one providing the attractive potential, and the other providing a repulsive potential forms a potential minima a small distance on the order of 200~nm from the fiber surface. Carefully selecting the wavelengths of the dipole trap, a magic wavelength condition [2] for Rydberg states can allow for the trapping of both the Rydberg and the ground state of the atoms in the same potential.

We present our results on the experimental excitation of Rydberg atoms next to an optical nanofiber and present the plans for extending our dipole trap for ground state atoms to also allow for the trapping of Rydberg atoms at the surface of the fiber, paving the way for experiments such as the investigation of 1D many body systems and the development of quantum gates.

1. Krishnapriya Subramonian Rajasree, Tridib Ray, Kristoffer Karlsson, Jesse L. Everett, and Síle Nic Chormaic, "Generation of cold Rydberg atoms at submicron distances from an optical nanofiber", Phys. Rev. Research 2, 012038(R), 2020

2. Jiandong Bai, Shuo Liu, Jun He and Junmin Wang, "Towards implementation of a magic optical-dipole trap for confining ground-state and Rydberg-state cesium cold atoms", J. Phys. B: At. Mol. Opt. Phys. 53, 155302, 2022

17:00 Towards a dual-species tweezer array of Na and Cs atoms

Optical tweezer arrays of neutral atoms provide a controllable and scalable platform for quantum computing and quantum simulation. Neutral atoms in these arrays interact via long-range van der Waals interactions, when excited into Rydberg states. A dual species array adds to the toolbox of atom arrays and allow for schemes involving multiple species. For example, non-destructive measurement, a key ingredient in quantum error correction, can be achieved by entangling “ancillary” qubits with “data” qubits and performing readout on the ancillary qubits. Having two distinct species to play the role of “data” and “ancilla” minimizes crosstalk when performing measurements on “ancilla” qubits or realizing gates between “data” qubits. We present our progress towards a dual species tweezer array platform using Na and Cs atoms. We stochastically load Cs atoms into static traps created by a spatial light modulator and can rearrange them into a desired defect-free pattern with high fidelity using traps formed by acousto-optic deflectors. We can perform Raman sideband cooling on the entire array. We also coherently excite atoms to the Rydberg state and see signatures of the interactions between the atoms.

17:00 Towards Implanting Radioactive Polar Molecules in a Noble Gas Matrix for Fundamental Symmetry Tests

Nuclear Schiff moments (NSMs) present a powerful probe into new physics through their connection to CP-symmetry violation. We are investigating the application of molecular matrix methods to NSM searches of radioactive isotopes, particularly radium-225, which has an enhanced Schiff moment resulting from its octupole deformations. These methods involve trapping polar molecules in a noble gas matrix, which is predicted to lock their orientation relative to the lattice vectors. In this contribution, we focus on the portion of the FRIB EDM$^3$ instrument, currently in the design stage, that will create and implant the polar molecules in the substrate. The instrument’s beamline starts with a spray-based ion source that will be used to efficiently ionize aqueous harvested radioisotopes. The spray will be collected by a dual ion funnel which will perform initial filtering of background ions. Then the ions will be analyzed by mass-to-charge ratio using a quadrupole mass filter, and then be neutralized in a charge-exchange cell. Finally, the molecules will be co-deposited along with a noble gas matrix. We will report on the design of this high-efficiency molecular beam source and the progress of its construction.

17:00 Towards magnetoassociation of the ultracold open-shell RbSr molecule

Ultracold dipolar molecules offer an ideal platform for investigations in the fields of quantum simulation, precision measurement and quantum chemistry. The range of possibilities offered by ultracold molecules could be substantially extended by employing the previously unexplored class of open-shell molecules like RbSr. Thanks to its unpaired valence electron RbSr possesses both a magnetic and an electric dipole moment offering an additional level of control with new exciting possibilities for quantum simulations.

Here we present our novel quantum-engineering approach towards the production of ultracold open-shell RbSr molecules that utilizes an ultra-narrow magnetic Feshbach resonance at 1311 G. Due to its extremely low relative width on the order of 10^-6, this is a serious experimental challenge. Our state-of-the-art dual stabilization approach to the control of magnetic fields now enables us to achieve a relative magnetic field stability at the ppm level at fields beyond 1000 G.

As a real-life benchmark of the capabilities of our system, we efficiently produce Rb Feshbach molecules on an ultranarrow 1.3-mG-wide resonance at 911.7 G. This is the first time that Feshbach molecule association is successful for such a narrow relative width and it is a crucial step towards the ultimate goal of magnetoassociating RbSr molecules.

17:00 Tracking the vector acceleration with a hybrid quantum accelerometer triad

Robust and accurate tracking of acceleration remains a challenging problem in many fields. For geodesy, geophysics or underground exploration, precise mapping of gravity requires the use of onboard gravimeters or gradiometers as well as inertial navigation systems to compute accurate positioning information from classical accelerometers and gyroscopes. Quantum sensors based on cold-atom interferometry hold enormous potential to provide such high-precision instruments. However, these inherently scalar sensors must be precisely aligned with the acceleration vector of interest. In this work, we present the first three-axis accelerometer exploiting the quantum advantage to measure the full acceleration vector (magnitude and direction). We demonstrate a high data rate (1 kHz) sensor with a magnitude accuracy below 10 $\mu g$, and a pointing accuracy of 4 $\mu$rad relative to each axis. This is achieved by sequentially applying three atom interferometer sequences along the mutually-orthogonal axes of a triad. By integrating navigation-grade classical accelerometers on each axis, we construct a compact and robust hybrid vector accelerometer. We characterize the ultra-low bias of our triad and track the gravitational acceleration vector over long timescales. We demonstrate a stability of $6 \times 10^{-8}~g$ on the vector norm after 24 h. This corresponds to a 50-fold improvement over that provided by our classical accelerometers. This paves the way toward future strapdown applications with quantum sensors and highlights their potential as future high-grade, inertial navigation units.

17:00 Training quantum denoisers

State preparation often suffers from various sources of device-dependant noise. It is hard to characterise and let alone mitigate the noise. Machine learning can be used to automate the denoising task. Quantum computers are the ultimate machines to process quantum signals. As such, we propose to use machine learning on quantum computers to denoise quantum data.

For this, we design a flexible family of trainable variational circuits that are capable of implementing arbitrary quantum channels. Due to the resemblance to their classical counterparts, we call these circuits quantum neutral networks (QNNs). We show that QNNs use the data efficiently and can be trained on imperfect devices even when part of the training data is corrupted.

We proceed to design QNN architectures that are tailored to cancel various types of noise. We show how quantum autoencoders can significantly reduce shot-to-shot noise. This is achieved without access to supervisory data and autoencoders can be trained once to denoise different highly entangled states. Then we turn our attention to extrapolation of parameters like temperature. We show how to train QNNs to produce states that are colder than any state seen during training. Finally, we develop recurrent QNNs for processing that requires memory. We use recurrent QNNs to design quantum bandwidth filters---a task greatly complicated by the no-cloning theorem. For recurrent networks, we further economize resources by combining quantum and classical processing.

Quantum denoisers offer a practical application of quantum computers to the experimental preparation of entangled states. This technology is particularly suited to an apparatus that already carries a highly-tunable quantum control system on board, such as quantum logic.

Based on: Nat. Commun. 11, 808; Phys. Rev. Lett. 124, 130502; PhD thesis: https://doi.org/10.15488/11050 and some work in progress.

17:00 Ultra-high vacuum chamber development for a Sr optical lattice clock with a Laguerre-Gaussian trapping geometry

Strontium optical lattice clocks (OLC) are a promising instrument for applications ranging from the redefinition of the second in the international system to geodesy and fundamental physics, for instance, dark matter detection, variation of fundamental constants, or general relativity tests. LNE-SYRTE, Observatoire de Paris operates two Sr OLCs with a systematic uncertainty on the order of $10^{-17}$, mostly limited by the inhomogeneous thermal distribution of the vacuum chamber inducing black body radiation (BBR) shift, but also by cold collisions between the atoms trapped in each site of the optical lattice.
Aiming to improve the characterization of systematic effects in optical lattice clocks below $10^{-18}$, we propose the implementation of Laguerre-Gaussian modes (LG$_{pl}$) to shape a multi-site trap in the 1D optical lattice of a Sr OLC. Hence reducing the density of atoms, while preserving the advantages of 1D lattices such as amplified power and spatial purity of the modes, unlike 3D optical lattices or tweezers. Quantitatively, the trapping potential in an LG$_{0l}$ mode is given by:
$U_{0l}(r,\varphi,z)=-U_0 e^{\frac{-2r^2}{w^2(z)}}\cos^2\left[kz-\psi_l(z)\right]\left(\frac{2r^2}{w^2(z)}\right)^{|l|}\cos^2(l\varphi)$
where $U_0 = \alpha_d I_0$, with $\alpha_d$ the atomic polarizability and $I_0$ the intra-cavity of the trapping light.
In this work, using a liquid crystal on silicon spatial light modulator (SLM), we demonstrate the generation of LG$_{0l}$ modes with $l$ up to 4, and the injection of these modes into an optical cavity placed in a new copper vacuum chamber. A Pound-Drever-Hall (PDH) scheme is then used to lock the cavity length to the LG$_{0l=0,1,2,3,4}$ modes. Trapping depths up to 39$E_r$ for an LG$_{04}$ were obtained, a priori making it possible to implement LG lattices within the clock sequence.
In addition, for limiting conductive and radiative exchanges between the experimental system and the laboratory, the thermal design of the new setup comprises an Ultra-High Vacuum (UHV) chamber that is also placed in a primary vacuum environment. The new thermal conditions will allow better control and determination of the contribution of the BBR to the clock transition $^1 S_0 - ^3P_0$ at a fractional uncertainty below $10^{-18}$.

17:00 Ultracold mixtures of Cr and Li atoms: theoretical prospects for controlled atomic collisions, LiCr molecule formation, and molecular precision measurements

We theoretically investigate interatomic interactions and ultracold collisions between chromium and lithium atoms. We use the coupled cluster and multireference configuration interaction methods to calculate the potential energy curves and the permanent and transition electric dipole moments for the quartet, sextet, and octet electronic states of the LiCr molecule correlated to the four lowest atomic dissociation limits. We find that the LiCr molecule in the $X\,^6\Sigma^+$ ground electronic state is strongly bound with the well depth of 8406(100)$\,$cm$^{-1}$ and has a large permanent electric dipole moment of 3.3$\,$D at an equilibrium distance of 4.87$\,$bohr, while the $a\,^8\Sigma^+$ first excited electronic states is weakly bound with the well depth of 565(18)$\,$cm$^{-1}$ and has a noticeable permanent electric dipole moment of $0.7\,$D at the equilibrium distance of 6.48$\,$bohr. We investigate the optical paths of forming deeply-bound LiCr molecules via photoassociation and stimulated Raman adiabatic passage. We propose precision measurements of the variation of electron-to-proton mass ratio using ultracold LiCr molecules. We predict the scattering lengths for the ultracold spin-polarized Cr+Li collisions (37$^{+29}_{-22}\,$bohr for $^{53}$Cr+$^6$Li) governed by the $a\,^8\Sigma^+$ electronic state without any adjustment to experimental data and in good agreement with recent experimental measurements. Finally, we calculate magnetically tunable Feshbach resonances for ultracold $^{52}$Cr+$^6$Li and $^{53}$Cr+$^6$Li collisions and assess prospects for magnetoassociation into polar and highly magnetic LiCr molecules. Present theoretical results may guide ongoing experimental studies on ultracold strongly-interacting mass-imbalanced Fermi-Fermi Li+Cr mixtures and LiCr molecules.

17:00 Upgrading the transportable optical lattice clock at PTB

After laboratory optical atomic clocks have reached fractional frequency uncertainties in the 10$^{-18}$ regime, it is an ongoing task to miniaturize these complex clocks and make them transportable and in-field deployable, without compromising their performance. This effort is primarily motivated by promising prospects in geodesy. Together with accurate frequency transfer via fiber links, these clocks can measure gravitational potential differences in the 0.1 m$^2$/s$^2$ regime (corresponding to 'cm' height differences on Earth’s surface) with high spatial and temporal resolution. Thus, they could be used to establish an accurate height reference system. At PTB, we have been operating a transportable optical clock based on neutral strontium atoms in a 1-D optical lattice. This clock previously had been to international measurement campaigns in Modane, Turin, Paris, and Munich.
Here we present the progress in the development of our new transportable clock, to achieve a lower uncertainty and better instability. These upgrades come in the form of a new physics package employing a single-beam pyramid MOT for the first and second stages of cooling, better stray magnetic field shielding, a lower background pressure in the science chamber and a temperature shield for better thermal uniformity during the clock interrogation phase. These changes along with the use of a new transportable cavity (instability: 1.6 × 10$^{-16}$) operating at the subharmonic of the clock transition are expected to push the fractional frequency uncertainty to the low 10$^{-18}$ regime.

This work receives funding from the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy - EXC-2123 QuantumFrontiers - 390837967 and SFB 1464 TerraQ - 434617780. It is supported by the Max Planck-RIKEN-PTB Center for Time, Constants and Fundamental Symmetries.

17:00 Velocity Selective Resonances from a Novel Optical Force

Optical forces on atoms derive from the momentum exchange between the atoms and an incident light field [1]. Atoms cannot absorb the linear momentum of light into their internal coordinates the same way as energy ($\hbar \omega_{\ell}$) and angular momentum ($\Delta \ell = \pm 1$), so absorption or emission must involve atomic motion, usually in the form of a recoil momentum $\Delta p \equiv \hbar \omega_{\ell}/c \equiv \hbar k$. Since this is small compared to typical atomic momenta, it must be repeated many times to make a significant velocity change. Typically an excitation is followed by a spontaneous emission and then repeated to achieve the multiple momentum exchanges. The strength of such optical forces on atoms depends on the rate of this exchange and this is usually limited by the excited state lifetime $\tau$, so the force scales with $\Delta p/\Delta t = \hbar k/\tau \equiv \hbar k \gamma$. In practice, excitation also takes time so the maximum value of this radiative force is given by $F_{\mathrm{rad}} \equiv \hbar k \gamma/2$ for light tuned on resonance.

Instead of spontaneous emission, we have been using stimulated emission to increase the momentum exchange rate, where we choose the stimulating light to have a $\vec{k}$-vector opposite to that of the exciting light so that the net momentum transfer becomes $2 \hbar k$. A rapidly cycling, absorption-stimulated emission sequence from counter-propagating beams can lead to a very large force [2], $F_{\mathrm{ARP}} \gg F_{\mathrm{rad}} \equiv \hbar k \gamma/2$. We use a series of properly tailored pulses designed to cause absorption-stimulated emission cycles that produce a strong, unidirectional force. The optical frequency of each pulse is swept to enable adiabatic rapid passage (ARP) because such pulses invert populations more efficiently than $\pi$-pulses. Such ARP forces have been demonstrated for atoms initially at rest to be much stronger than ordinary radiative forces [3-7]. We have explored how this very strong force depends on atomic velocity and found surprising enhancement at certain regularly-spaced velocities [7,8]. These will be discussed, but they seem to occur when atoms travel approximately an integer number of wavelengths between ARP pulses.

In our experiments, a well-collimated beam of atoms is deflected by the ARP force and their spatial distribution is recorded by an MCP-phosphor-screen combination. Because the atoms have a significant longitudinal velocity spread that is unaffected by the light beams, their spatial distribution is spread out. Nevertheless, there are distinct, regularly spaced peaks at velocities that approximately correspond to "resonant" velocities.

An important criterion for a cooling force is a velocity dependence that is finite over some velocity range but vanishes at other velocities so that atoms accumulate in the region of velocity space where the force is zero or very small. Atomic motion in the lab frame corresponds to Doppler-shifted frequencies in the atomic frame, so we use oppositely detuned laser beams to simulate a velocity $v_{at}$. For large $v_{at}$ we use two different lasers, but the coherent momentum exchange requires phase locking them \footnote{J. Elgin, Ph.D Thesis, Stony Brook University, 2015.}. This has been implemented and the first results show that the force is nearly constant at low $v_{at}$ but decreases at higher $v_{at}$. For an ARP frequency sweep range of $\pm \, \delta_0$, one intuitively expects an effective force range of $v_{at}$ between 1/4 and 1/2 of $\pm \, \delta_0/k$, and our initial measurements corroborate this.

[1] H. Metcalf and P. van der Straten, Laser Cooling and Trapping (Springer Verlag, NY, 1999).
[2] A. Goepfert, I. Bloch, D. Haubrich, F. Lison, R. Schutze, R. Wynands, and D. Meschede, Phys. Rev. A 56, R3354 (1997).
[3] T. Lu, X. Miao, and H. Metcalf, Phys. Rev. A 71, R 061405 (2005).
[4] X. Miao, E. Wertz, M. G. Cohen, and H. Metcalf, Phys. Rev. A 75, 011402 (2007).
[5] X. Miao, Ph.D. thesis, Stony Brook University (2006).
[6] T. Lu, X. Miao, and H. Metcalf, Phys. Rev. A 75, 063422 (2007).
[7] We acknowledge laboratory help from Brian Arnold, Mike Dapolito and Eric Jones
[8] J. Elgin, Ph.D Thesis, Stony Brook University, 2015.

17:00 Very long baseline atom interferometry for tests of fundamental physics

Atom interferometry is based on the measurement of phase differences in coherent matter waves. As such, it is an ideal technique for measuring inertial forces caused by e.g. acceleration and rotation. The precision of the measurements is provided by the standing light wave imprinting its position-dependent phase onto the matter waves and therefore acting as a fine-spaced ruler.

Being based on single atoms in superposition states, atom interferometry based sensors can perform non-classical measurements and new perspectives for tests of fundamental physics. They have the ability to probe the limits of quantum physics and general relativity, though this requires highly precise and well-controlled devices.

Here we report on the commissioning of the Very Long Baseline Atom Interferometry (VLBAI) facility in the Hannover Institute of Technology. It will be composed of a 10.5 m high magnetically shielded free-fall baseline, two atomic source chambers featuring Bose-condensed rubidium and ytterbium, as well as a high-performance seismic attenuation system. This allows for a variety of tests of fundamental physics in a well-controlled environment [1-3].

Besides presenting the current status of the facility we discuss its prospects for fundamental physics measurements. These include quantum clock interferometry for gravitational redshift tests [4] and differential dual-species interferometers for tests of the universality of free fall [5], but also tests of macroscopicity and fundamental decoherence by separation of superposition states on the meter scale [6].

[1] D. Schlippert et al, arXiv:1909.08524 (2019)
[2] É. Wodey et al, Review of Scientific Instruments 91, 035117 (2020)
[3] M. Schilling et al, Journal of Geodesy 94, 122 (2020)
[4] F. Di Pumpo et al, PRX Quantum 2, 040333 (2021)
[5] J. Hartwig et al, New Journal of Physics 17, 035011 (2015)
[6] B. Schrinski et al, Physical Review Research 2, 033034 (2020)

17:00 Waveguide QED with Rydberg superatoms

Rydberg quantum optics allows to create strong optical nonlinearities at the level of individual photons by mapping the strong dipolar interactions between collective Rydberg excitations onto optical photons. The interactions lead to a blockade effect such that an optical medium smaller than the blockaded volume only supports a single excitation which is collectively shared amongst all blockaded atoms forming a ‘Rydberg superatom’. Thanks to the collective nature of the excitation, the superatom effectively represents a single emitter with a strongly enhanced coupling to few-photon probe fields with directional emission into the initial probe mode [1].

This makes Rydberg superatoms an ideal platform to study the interaction of individual two-level emitters with quantised light fields. The interaction leads for example to the emergence of two- and three-photon correlations in the transmitted light, while exchange interactions between the constituent atoms within a superatom lead to non-trivial decay dynamics of the collective state [2].
When combined with controlled dephasing into dark, collectively excited states, we exploit the strong photon-emitter coupling to subtract exact photon numbers from incoming light fields providing a means to precisely manipulate their quantum state [3]. To this end, we cascade multiple superatoms in 1D chain along mode of the probe field. In the regime of low dephasing, such a cascaded quantum system of multiple superatoms also offers the prospect to observe photon-mediated interactions and entanglement along the probe mode which effectively forms a freespace ‘waveguide’.

We also provide a brief outlook on a new cryogenic experimental platform in which we plan to study hybrid quantum systems of Rydberg atoms combined with e.g. electromechanical oscillators or integrated photonic and microwave circuits.

[1] A. Paris-Mandoki, C. Braun, J. Kumlin, C. Tresp, I. Mirgorodskiy, F. Christaller, H. P. Büchler, and S. Hofferberth, Phys. Rev. X 7, 041010 (2017).

[2] N. Stiesdal, H. Busche, J. Kumlin, K. Kleinbeck, H. P. Büchler and S. Hofferberth, Phys. Rev. Research 2, 043339 (2020).

[3] N. Stiesdal, H. Busche, K. Kleinbeck, J. Kumlin, M. G. Hansen, H. P. Büchler and S. Hofferberth, Nat. Commun. 12, 4328 (2021).

17:00 Zeeman-Sisyphus Deceleration of Polyatomic Molecules

Polyatomic molecules can provide improvement over diatomic systems in cold chemistry, precision measurement of fundamental physics, and quantum information. Slowing these species to trappable velocities is a major limitation in realizing these applications. Over the past decade, radiative slowing methods have been successfully applied to diatomic and, recently, triatomic molecules with highly diagonal Frank-Condon factors. Alternative slowing methods are needed for molecules that are less favorable for scattering the ~10,000 photons required for radiative slowing. Here we present a superconducting-magnet-based Zeeman-Sisyphus decelerator that requires fewer than 10 photon scatters to slow molecules to velocities suitable for loading a MOT, magnetic, or electric trap. We describe the design considerations, apparatus construction, and application of the slower to both CaOH and YbOH molecular beams. We also discuss the generalizability of this slowing method to increasingly complex molecular species.

Thursday 21 July

08:00 → 08:45 Exhibitors: Exhibitor Show Hours 8am-5:30pm (Last Day!)

Exhibitors and vendors available

08:00 → 08:45 Registration / Info Desk open 8:00am - 5:30pm

08:45 → 10:30 Plenary session

10:30 → 11:00 Coffee Break

11:10 → 12:20 Plenary session

14:00 → 15:10 Plenary session

15:10 → 15:40 Break

15:50 → 17:00 Plenary session

17:00 → 18:30 Poster session: Thursday

17:00 $0^-_g$ potential in Cs$2$, revisited: observation of missing levels.

We use photoassociation of spin polarized ($F=3$, $m_f=3$), ultracold cesium atoms confined in a 1D optical lattice to confirm the existence of the two lowest lying vibrational levels in the $0^-_g$ pure long-range molecular potential of Cs$_2$. The observation of these two levels confirms the theoretical predictions of Bouloufa et al. [1] postulating that the numbering of vibrational levels of this potential needs to be shifted by two in order to agree theory with experimental data. We also provide unambiguous evidence that the work of Zhang et al. [2] which claimed priority of observing these new levels, in fact observed levels belonging to the $0^+_u$ molecular potential.

Due to the expected low molecular formation rate we have implemented Feshbach resonance-enhanced association of molecules in $v = 0$ and $v = 1$. Several of such resonances are present at fields below 70 G but the newly discovered vibrational levels could be detected only in the vicinity of the Feshbach resonance at 19.9 G [3].

We have determined the binding energies of the ($v$,$J$) = $(0,2)$, $(1,0)$, $(1,2)$ and $(1,4)$ with absolute accuracy better than 1 MHz by referencing the photoassociation laser to a frequency comb. For the $v = 1$ level we have extracted the rotational constant of ~56 MHz.

[1] Bouloufa, N., Crubellier, A., & Dulieu, O. Phys. Rev. A, 75(5), 052501(2007)
[2] Zhang, Y., Ma, J., Wu, J., Wang, L., Xiao, L., & Jia, S. . Phys. Rev. A, 87(3), 030503(2013)
[3] Tolra, B. Laburthe, et al. EPL (Europhysics Letters) 64.2 (2003): 171

17:00 A resonance facilitated three-channel model for p-wave scattering

We have shown that two-channel Feshbach theory works well to describe p-wave Feshbach resonances [1], however a peculiar result of a non-intuitive molecular magnetic moment led to the realization that an additional shape resonance was part of the scattering problem and unaccounted for.
We study how two shape resonances in separate hyperfine channels in Potassium-40 interact with a Feshbach resonance. To account for all resonances, we need (at least) a three-channel model. This is theoretically and computationally highly involved.
However, as full coupled-channels calculations reveal a strong magnetic field dependence of the atom loss between the two hyperfine channels that contain the shape resonances, we approximate the coupling between the shape resonances to be purely facilitated by the Feshbach channel.
This greatly simplifies the three-channel model and allows us to retrieve the standard Breitt-Wigner form of the scattering matrix with corrected values of the resonance width and resonance shift resulting from the presence of the third channel. We reveal that, contrary to the resonant two-channel model used in our previous analysis [1], the resonance-facilitated three-channel model can consistently match full coupled channels calculations with physically realistic input parameters.
Hence, it captures physics beyond the reach of the standard two-channel Feshbach approach.

[1] D. J. M. Ahmed-Braun, K. G. Jackson, S. Smale, C. J. Dale, B. A. Olsen, S. J. J. M. F. Kokkelmans, P. S. Julienne, J. H. Thywissen, Probing open- and closed-channel p-wave resonances, Phys. Rev. Research 3, 033269 (2021).

17:00 AION: An atom interferometer observatory and network

Atom interferometers are sensitive to the signatures of gravitational waves, ultra-light dark matter and other fundamental physics phenomena. The development of this new class of quantum detector will complement traditional detection methods and extend measurement capabilities.

The Atom Interferometer Observatory and Network (AION) [1] is a planned series of atom interferometers operating on the strontium clock transition in a gradiometer configuration. The baseline of terrestrial devices, corresponding to the separation between interferometers in the differential measurement, will increase from 10 m to 1 km. Current work focusses on developing the cold atom technologies to support the detection goals, including transport and cooling of the atom clouds, state preparation and large momentum transfer techniques, and design of the 10 m device. This poster outlines the scientific goals, experimental implementation and recent progress of the AION detector with a focus on the work on atom transport and cooling being carried out at the University of Cambridge.

This poster is presented on behalf of the AION consortium.

[1] L. Badurina et al. “AION: An Atom Interferometer Observatory and Network”, Journal of Cosmology and Astroparticle Physics 5, 011 (2020).

17:00 An Atomic Fabry-Perot for the Generation and Measurement of Ultracold Wavepackets

A matter-wave Fabry-Perot (FP) for the generation of ultracold wavepackets could be implemented using an optical double barrier. Observation of the transmission spectrum of a single such FP becomes impractical for wavepacket temperatures above about 100pK. The resonances are washed out due to the velocity width of the incident wavepacket being larger than the width of the resonances. We propose a scheme for using a second atomic FP with a tunable cavity length to characterize the filtering properties of the first. Gross-Pitaevskii (GP) simulations of a 87Rb BEC interacting with double-Gaussian potentials show that evidence of resonant transmission can be observed using this scheme. The GP simulations use experimentally achievable parameters of a 1nK 87Rb BEC of a few thousand atoms, incident on barriers with a 1/e^2 radius of 1.3 µm. With these parameters, BECs containing a few hundred atoms could be generated at a temperature less than 50pK. We plan to realize this scheme experimentally using a spatial light modulator to manipulate the optical potential for the tunable cavity length matter-wave FP.

*NSERC and the Fetzer Franklin Fund of the John E. Fetzer Memorial Trust

17:00 An experiment to measure the electron's electric dipole moment using trapped ultracold molecules.

The large asymmetry between matter and antimatter in the Universe is a mystery. The formation of this extra matter requires charge parity (CP) violation beyond that contained in the standard model, and therefore points towards new physics [1]. The electron’s electric dipole moment (eEDM) is sensitive to this new physics. Precision measurement of the eEDM tests physics beyond the Standard Model and will expand our understanding of the fundamental principles of nature. We aim to improve the precision of the eEDM measurement by 3 orders of magnitude using an array of ultracold ytterbium monofluoride (YbF) molecules held in an optical lattice, measuring an eEDM on the order of 10$^{-32}$ e cm [2].

We produce a beam of YbF using a two stage cryogenic buffer gas source cooled to 2 K. In this source, YbF is formed by laser ablation of an ytterbium target in the presence of sulphur hexafluoride (SF6), and is then entrained in a flow of cold helium gas. We plan to decelerate these molecules using laser slowing, capture them in a magneto-optical trap, cool them to a few microkelvin and then load them into an optical lattice where spin coherence times of several seconds seem feasible. We will present the progress made towards generating a slow beam, initial laser slowing experiments and our plans for the future.

[1] Sakharov A D 1991 Sov. Phys. Usp. 34 392–3
[2] N J Fitch et al 2021 Quantum Sci. Technol. 6 014006

17:00 Analyzing the hyperfine structure using the quantum orbit eccentricity

The old problem of the discrete spectrum of the hydrogen atom obeys a SO(4) symmetry, which is isomorphous to two subgroups that obey the algebra of angular momentum. The algebraic structure allows us to formulate a basis closely related to the properties of the wave function in parabolic coordinates. On the other hand, the properties of other angular momenta, such as electron spin and nucleus spin, are introduced by adding angular momentum. All these contributions are known as the hyperfine structure. In this work, we explore the symmetries of the problem to analyze the atomic hyperfine structure strictly using the properties of the SO(4) group of the Laplace-Runge-Lenz vector. Additionally, we have done a brief analysis of the symmetry breaking in the presence of electric and magnetic fields.

17:00 Big Time Crystals in a Bouncing BEC

Discrete time crystals created in a Bose-Einstein condensate (BEC) bouncing resonantly on a periodically driven atom mirror can involve dramatic breaking of discrete time translation symmetry [1] with response periods up to s  100 times the driving period T [2]. This allows the creation of big time crystals having a large number of temporal lattice sites. By choosing suitable Fourier components in the periodic driving of the atom mirror, such a system enables effective potentials to be constructed in time lattices with nearly any shape, which provides a flexible platform for realising a broad range of condensed matter phenomena in the time dimension. Predicted phenomena include topologically protected edge states in time, Mott insulator states in the time dimension, and time crystals exhibiting temporal disorder, quasi-crystalline order and exotic long-range interactions [3].

Here, we report experimental progress towards creating big time crystals in a bouncing potassium-39 BEC system. The BEC is prepared in a 1064 nm crossed optical dipole trap above an oscillating 532 nm light-sheet atom mirror, which is driven with frequency corresponding to the selected s : 1 resonance for a given drop height and with amplitude adjusted to produce stable resonance islands located around periodic orbits with period sT. The BEC is then released from the optical dipole trap to fall on to the oscillating mirror under strong transverse confinement. When the particle interaction is raised above a critical value to spontaneously break the time-translation symmetry, a stable localized wave-packet evolves without tunnelling to other wave-packets, i.e., a discrete time crystal is formed.

1. K. Sacha, Phys. Rev. A 91, 033617 (2015).
2. K. Giergiel, T. Tran, A. Zaheer, A. Singh, A. Sidorov, K. Sacha and
   P. Hannaford, New J. Phys. 22, 085004 (2020).
3. K. Sacha, Time Crystals, Springer (2020).

17:00 Bosons in novel lattices: discontinuous quantum phase transitions and the Bose glass

Quantum phase transitions occur at temperatures close to absolute zero and are driven by quantum fluctuations. One paradigmatic example is the change from a superfluid to a Mott insulator of ultracold bosons. This transition typically is continuous, i.e., the system undergoes a smooth change.

Using a resonantly shaken lattice, we could however turn the Mott transition into a discontinuous or first-order transition [1]. By modulating the position of the lattice, we hybridize the lowest two bands and drive a transition between a Mott insulator and a $\pi$-superfluid with a staggered order, where atoms dominantly occupy the band edge. Crucially, the transition can be discontinuous, as the non-staggered order in the Mott insulator is incompatible with the staggered order of the $\pi$-superfluid.

Furthermore, we observe metastability and hysteresis associated with the discontinuous transition, by monitoring how fast one phase changes into another. After crossing the discontinuous phase transition, the system remains in its initial, now metastable state, instead of following the evolution of the ground state. The eventual decay from the metastable state due to quantum fluctuations would be analogous to the false vacuum decay in the early universe.

In disordered or quasiperiodic media, the propagation of matter waves will be affected by (quasi)random interferences, forming a localized state known as the Anderson insulator. In the Bose-Hubbard model, the combination of interactions and disorder can give rise to the Bose glass phase, an insulating but compressible phase without long-range order that sits between the superfluid and the Mott insulator.

We have created a two-dimensional optical quasicrystal [2] and observed Anderson localization of non-interacting bosons above a critical lattice depth [3]. The interplay of disorder and interactions significantly shifts the transition from the superfluid to the Bose glass. Our realization of this transition in the optical quasicrystal opens a new avenue to exploring intriguing transport phenomena and many-body localization in two dimensions.

References:
[1] Bo Song et al. Realizing discontinuous quantum phase transitions in a strongly correlated driven optical lattice, Nature Physics 18, 259–264 (2022).
[2] Konrad Viebahn et al. Matter-wave diffraction from a quasicrystalline optical lattice, Phys. Rev. Lett. 122, 110404 (2019).
[3] Matteo Sbroscia et al. Observing localisation in a 2D quasicrystalline optical lattice, Phys. Rev. Lett. 125, 200604 (2020).

17:00 Can dipolar interaction shield dipolar relaxation?

There has been a long-term effort in reducing inelastic losses in quantum gases, from dipolar relaxation in spin mixtures to reactive collisions in molecules. For the first time we show shielding between atoms via the dipolar interaction and strong confinement. This has been achieved with bosonic dysprosium and resulted in an order of magnitude suppression of dipolar relaxation. Theoretical and experimental aspects will be presented.

17:00 Cavity-induced density wave ordering in strongly correlated Fermi gases

The interplay of pairing with density wave order is one of the most prominent feature of strongly correlated electronics systems, such as high temperature superconductors. We have realized a Fermi gas with short and long range interactions, independently and simultaneously controllable. Starting from a quantum degenerate, unitary Fermi in a cavity [1-4], we pump the system from the side in the dispersive regime to yield a tunable photon-mediated interaction that favors the self-organization of atoms into a density wave order. We show that this interaction is broadly tunable, and study the onset of density wave ordering in the crossover from BEC to BCS. Our observations are compared with a mean field theory. Our system offers a new way to study competing orders in strongly correlated matter.

[1] K. Roux, H. Konishi, V. Helson, and J.-P. Brantut, “Strongly correlated Fermions strongly coupled to light,” Nat Commun, vol. 11, no. 1, p. 2974, Jun. 2020, doi: 10.1038/s41467-020-16767-8.
[2] K. Roux, V. Helson, H. Konishi, and J. P. Brantut, “Cavity-assisted preparation and detection of a unitary Fermi gas,” New J. Phys., vol. 23, no. 4, p. 043029, Apr. 2021, doi: 10.1088/1367-2630/abeb91.
[3] H. Konishi, K. Roux, V. Helson, and J.-P. Brantut, “Universal pair polaritons in a strongly interacting Fermi gas,” Nature, pp. 1–5, Aug. 2021, doi: 10.1038/s41586-021-03731-9.
[4] V. Helson, T. Zwettler, K. Roux, H. Konishi, S. Uchino, and J.-P. Brantut, “Optomechanical Response of a Strongly Interacting Fermi Gas,” arXiv:2111.02931 [cond-mat, physics:physics, physics:quant-ph], Nov. 2021, [Online]. Available: http://arxiv.org/abs/2111.02931

17:00 Characterization of high-fidelity Raman qubits

In quantum information and computation, very high fidelity of gate operations is required. Measuring tiny gate errors with high accuracy is a difficult task, which is traditionally done by randomized benchmarking.
In this work we present a new method which allows to determine the gate errors of Raman qubits, in which the qubit states are coupled in a Raman transition via another state, thereby forming a three-state chainwise-connected system. The method is based on the repetition of the same gate sufficiently many times and thereby amplifying the tiny error to easily measurable sufficiently large values.
In order to deduce the gate error from the amplified error, analytic connections between the single-gate and multi-gate propagators are derived for three-state Raman systems with two types of symmetries:
Majorana and Morris-Shore. We extend these connections to arbitrary dimensions which paves the path toward tomography of qudits.

17:00 Chasing the last bit of STIRAP efficiency between metastable helium and Rydberg state.

Using laser pulses to manipulate the internal quantum states of atoms and molecules provides new opportunities to create novel quantum devices. Coherent population transfer is the fundamental tool for many potential quantum applications such as atomic lithography, Rydberg arrays, and quantum information processing. We describe the Rydberg state excitation in a three-level system through Stimulated Raman Adiabatic Passage (STIRAP) and an excitation efficiency measurement method with bichromatic force. Theoretically, STIRAP can produce 100% population transfer, but it is typically far less efficient in practice. We will discuss the potential reasons for efficiency loss in three-level population transfer, especially the effect of velocity spread in atomic beam, and the solutions to overcome the efficiency loss.

17:00 Continuous Cold Strontium Atoms through a Cavity as a Frequency Standard

The state-of-the-art optical atomic clocks rely on trapping, cooling and readout at the same point in space and the cooling stages are separated in time; however, they suffer from finite dead-time between measurements leading to additional noise, and complicated control sequences. The next generation of optical clocks should be continuous with inherently zero dead-time and steady-state operation which simplifies control.
We plan to demonstrate this with a continuous beam of neutral strontium-88 that is cooled and compressed by a sequence of laser cooling stages separated in space. The continuous beam emerges from a Zeeman slower with a speed around 30$\,$ms$^{-1}$ and enters an angled 2D MOT which will act to (1.) cool and compress the atomic beam transversely (2.) deflect the atomic beam into a cavity region that is protected from harmful stray light (3.) focus the atomic beam in 1 axis to overlap with the mode volume of a linear cavity. With this continuous, compressed, cooled and dense fluxed of atoms through the cavity, we plan to perform spectroscopy on the 7.6$\,$kHz wide inter-combination line with a cavity enhanced scheme called NICE-OHMS that is immune to cavity noise (to first order), and then characterize the experiment's performance as a frequency standard.

17:00 Controlled Interactions between Ultracold KRb Molecules in Two Dimensions

Dipolar molecules in two dimensions are a powerful platform for the study of quantum many-body physics, thanks to their long-range, anisotropic dipolar interactions. We have developed key experimental capabilities required for the study of such systems, including layer-resolved state control and detection, field-tunable dipole orientation and strength, and control of both intralayer and interlayer interactions. The interactions between layers are probed through chemical reactions mediated by exchange of rotational excitations. The reaction rate is controlled through application of an electric field gradient, revealing an interplay between the thermal energy and spin exchange. Within a layer the interactions realize a spin Hamiltonian, where the Ising and exchange interactions are controlled through electric field strength and orientation, and molecular rotational state. The interactions manifest through shifts in the rotational transition frequency and decays in the Ramsey contrast. We discuss the outlook for the platform, including a path towards creation of a spin squeezed state.

17:00 Creating and measuring sub-wavelength volumes using quantitative absorption imaging of optically dense ensembles

Quantum gas microscopes have become a major element for quantum simulations using ultra-cold atoms in optical lattices. They are for example used to observe long-range order such as anti-ferromagnetic correlations in far field optical lattices using density and spin resolved microscopy. Decreasing the period of such lattice offer interesting perspective to increase atom-atom interaction energies and engineer atom-light coupling that our group tackles via the hybridization of cold atoms and nano-structured surfaces.
In this poster, we will present how such type of sub-wavelength lattice potentials can be generated by trapping atoms in proximity (tens to hundreds of nanometers) of a nano-structured surface. At such atom to surface distance, the attractive Casimir-Polder force can be compensated by a doubly dressed state trapping method that I will discuss. Such method additionally offers solutions to overcome the diffraction limit of conventional imaging that become critical for sub-wavelength lattices. In this work, I will present the experimental characterization of a sub-wavelength resolution absorption imaging applicable to quantum gas detection. This method requires a quantitative determination of the atom number of dense clouds which has been characterized in this work and demonstrate that the scattering cross section reduces linearly with the optical density. Modelling the propagation of light in dense cloud we show that this reduction can be attributed to re-scattering of the incoherent part of the resonant fluorescence spectrum.
The poster will additionally present an update on our recent work on the spectroscopy of Acetylene in sealed hollow core fibers.

17:00 Deflection of barium-monofluoride molecules

Density-matrix simulations of an optical scheme for producing a large optical force on barium-monofluoride (BaF) molecules are presented. The scheme uses short laser pulses to induce excitation to the A Pi 1/2 state, with pulses from counter-propagating laser beams causing stimulated emission back to the ground electronic state. A magnetic field is used to remove degeneracies to avoid dark states. The calculated force is an order of magnitude larger than the maximum force possible with CW laser schemes. Additionally, because the molecules spend little time in the excited state, spontaneous decay is minimized, reducing or eliminating the need for re-pump lasers from other states (e.g., other ground vibrational states). Methods for electrostatic deflection of BaF will also be presented. The EDMcubed scheme [1] for measuring the electron electric dipole moment using BaF embedded in an Ar solid requires a BaF deflection to separate BaF from other products produced in a buffer-gas laser-ablation source.

[1] A. C. Vutha, M. Horbatsch and E. A. Hessels, Phys. Rev. A 98, 032513 (2018).

17:00 Dicke superradiance in arrays of multilevel atoms

We investigate the physics of Dicke superradiance with multilevel atoms. Dicke superradiance is a dissipative many-body phenomenon where excited atoms collectively emit a short and intense burst of light. While this physics is well understood for two-level systems in a cavity, our work involves extended arrays of multilevel atoms in free space. In previous work, we showed that Dicke superradiance generically occurs for two-level systems in arrays, provided that the distance between them is sufficiently small. Here, we consider atoms that can decay into multiple states and show that a superradiant burst can be emitted on all transitions. We develop constraints on the relative rates of each transition, and on the geometry of the atomic ensemble, and show that the intensity emitted in particular directions features a superradiant burst in arrays of large interatomic spacing. Our results provide a guide to explore this many-body phenomenon in state-of-the-art experimental setups.

17:00 Direct frequency comb spectroscopy with two atom species for comb laser frequency stabilization

1. Introduction
To convert a femtosecond laser into a frequency-comb laser, it is frequently essential to use a costly atomic clock [1] to stabilize the repetition rate (f rep) and sophisticated nonlinear optics to lock the offset frequency (f ceo). In this report, we demonstrate that the mode frequencies of a comb laser can be directly referenced to two stepwise two-photon transitions (STPTs) in cesium and rubidium using just one 6-cm cesium-rubidium mixed cell and no extra clocks, revealing a new approach for comb laser frequency stabilization. The related spectra are based on a novel scheme for reducing the residual Doppler background in direct comb laser spectroscopy. For showing the possibilities of being a comb clocks, we investigate all potential error causes to demonstrate that our comb laser is capable of serving as a time-keeping equipment in the 778 nm to 822 nm wavelength range. The ultra-high spectral resolution (5 kHz) of our direct comb laser spectroscopy reveals some new and intriguing physics, such as the two-pathway interfered dip in rubidium spectra; the abnormal light shift and collision shift compared to what was observed by CW laser; a narrower linewidth despite the presence of broadening intermediate states; and the zero influence of the laser bandwidth, in contrast to the "strong-influence" conclusion in the direct two-photon transition experiment [2].
2. Experimental setup and result
Fig. 1 (a) depicts the schematic diagram of our experimental arrangement. The spectra concurrently resolved by our comb laser are shown in Fig. 1 (b). The two STPTs as the frequency references are line 7 in rubidium and line 8' in cesium, which are 5S1/2(F=1)>5P3/2(F=2)>5D5/2(F=3) and 6S1/2(F=3)>6P3/2(F=3)>8S1/2(F=3), respectively. To generate Doppler-free spectra, a piezoelectric transducer (PZT) in fig. 1 (a) was utilized to constantly change the overlapping condition of the laser beam, allowing only the fluorescence arising from the overlapped counter-propagating pulses to be amplitude modulated. In Fig. 1 (c), When compared to the CW laser experiment [3] (black line), the AC Stark shift of Rb line 7 (green line) indicates a completely different direction of detuning, although the slope of the comb laser light shift (red line) in Cs line 8' is close to that of the CW laser [4]. In addition, the authors of reference [2] report a new error source in comb laser spectroscopy frequency accuracy; that is, the laser bandwidth or shaped pulses influence the atomic transition center as well as the linewidth in their comb-DTPT (direct two-photon transition) spectrum, whereas we did not find any such frequency shift in our STPT spectra, within our experimental resolution.

3. References
[1] R. Felder, Metrologia 42, 323-325 (2005)
[2] I. Barmes, S. Witte and K. S. E. Eikema, Phys. Rev. Lett. 111, 023007 (2013).
[3] C. S. Edwards, G. P. Barwood, H. S. Margolis, P. Gill, and W. R. C. Rowley, Metrologia 42(5), 464-467 (2005).
[4] C. M. Wu, T. W. Liu, M. H. Wu, R. K. Lee, and W. Y. Cheng, Opt. Lett. 38(16), 3186–3189 (2013).

17:00 Direct Laser Cooling of YO Molecules

"Ultracold molecules are poised to open many important applications, ranging from quantum information science to precision tests of fundamental physics. In the past decade, direct laser cooling of molecules has successfully achieved magneto-optical trapping, sub-Doppler cooling, and confinement in conservative optical traps. A key research direction for molecule-based quantum science requires achieving a high phase space density. We have recently demonstrated the highest phase-space density in a bulk gas of laser cooled molecules[1]. We are working on further increasing the phase space density of YO molecules by optimizing the scattering rate of the slowing scheme and MOT parameters. We will present our latest work in this direction and also discuss a scheme to utilize narrow-line cooling on an intermediate low–lying A’2Δ3/2 state, after cooling the YO molecules by gray molasses to a few microkelvin temperature.

[1] Y. Wu et. Al Phys. Rev. Lett. 127, 263201 "

17:00 Dynamical phases of matter in a periodic driven atom-cavity system

We report realizations of various dynamical hybrid light-matter phases, as a discrete dissipative time crystal [1], dynamical bond density wave phase [2-4], and limit cycle phase [5], by strongly coupling an atomic quantum gas to the light field of an optical cavity. The key feature of the cavity is a very small field decay rate ($\kappa / 2\pi$ = 3.6kHz), which is in an order of the recoil frequency ($\omega_{rec}/2\pi$ = 3.6kHz). This leads to a unique situation where cavity field evolves with the same timescale as the atomic density distribution, which is called a recoil resolved regime. For standing wave pumping, transversely with respect to the cavity axis, the system undergoes a phase transition from a normal homogeneous phase to a superradiant self-organization phase, accompanied by spontaneously breaking of Z2 symmetry. Modulating the amplitude of the pump field leads to the realization of a dissipative discrete time crystalline phase, whose signature is a rigid sub-harmonic oscillation between the two symmetry broken states [1]. On the other hand, shaking the pump potential by modulating the phase of the pump field give rise to an incommensurate time crystalline phase [3], whose dynamics can be captured by a non-standard three-level Dicke model [2, 4]. The phase modulation can also be used to create a dark state by transferring the atoms to the $p-$band of the system, which has an anti-symmetric parity of the condensate wave function, and hence, the atoms decouple from the cavity field.
[1] H. Keßler et al., PRL, 127, 043602 (2021).
[2] J. G. Cosme et al., PRA 100, 053615 (2019).
[3] P. Kongkhambut et al., PRL 127, 253601 (2021).
[4] J. Skulte et al., PRA 127, 253601 (2021).
[5] P. Kongkhambut et al., arXiv:2202.06980 (2022).

17:00 eEDM-sensitive molecules trapped in neon ice

Improved searches for the electron electric dipole moment (eEDM) require large numbers of polar molecules with long spin coherence times. We report trapping of BaF molecules in cryogenic neon ice, with trap lifetimes exceeding two weeks. Laser-induced fluorescence measurements indicate that the molecules are only weakly perturbed compared to previous studies on atoms in inert solids. Our results open a path to optical spin polarization and precession measurements in BaF:Ne, aimed at developing an improved eEDM search experiment.

17:00 Effect of an optical dipole trap on resonant atom-light interactions

The optical properties of a fixed atom are exquisitely well-known and investigated. For example, one important phenomenon is that the atom can have an extraordinarily strong response to a resonant photon, as characterized by a resonant elastic scattering cross section given by the wavelength of the transition itself, $\sigma_{sc}\propto\lambda^2$. The case of a tightly trapped ion, where the ground and excited states are equally trapped, is also well-known. Then, the elastic cross section is reduced by a fraction corresponding to the square of the “Lamb-Dicke parameter”, while this same parameter also dictates the probability of inelastic scattering that gives rise to motional heating.

In contrast, there are many emerging quantum optics setups involving neutral atoms in tight optical dipole traps, such as coupled to nanophotonic waveguides and cavities or in atomic arrays, where the goal is to utilize efficient atom-light interactions on resonance. Often, while the ground state is trapped, the excited state may in fact be untrapped or even anti-trapped. Here, we systematically analyze the consequences that this unequal trapping has on reducing the elastic scattering cross section, and increasing the motional heating rate. This analysis may be useful to optimize the performance of quantum optics platforms where equal trapping cannot be readily realized.

17:00 Electric-field-controlled dipolar collisions between trapped polyatomic molecules

Polar symmetric top molecules offer a multitude of interesting research opportunities as their permanent electric dipole moment makes them interact strongly and anisotropically and allows manipulating them already with moderate static electric fields. This, together with their wealth of internal states, permits studies and applications ranging from cold dipolar collisions to quantum information processing and quantum simulation. While their complexity is a blessing from an application perspective, it also renders trapping polyatomic molecules, achieving high densities and understanding as well as controlling collisions a challenging task.
By combining [1] a cryogenic buffer-gas cell with a centrifuge decelerator and an electrostatic trap [2], we can now confine up to $2\times10^7$ CH${_3}$F molecules at a temperature of $\sim350$ mK for several seconds, achieving densities of up to $10^7/$cm$^3$. Such high densities allow for the observation of collisions between the trapped molecules [3]. An ab-initio theory, taking into account both elastic and inelastic collisional loss channels, shows excellent agreement with our experiment and allows for the identification of dipolar relaxation as the major loss mechanism, accounting for $\sim95\%$ of the observed losses. We obtain inelastic rate constants below $4\times10^{-8}$cm$^3$/s and control and suppress the losses by tuning a homogeneous control field covering a large fraction of the volume of the trap. As understanding and suppression of these inelastic losses is imperative to proceed towards higher phase-space densities, our findings are immediately relevant for cold molecular collision studies and are an important step towards the observation of re-thermalisation between polyatomic molecules.

[1] X. Wu et al., Science 358, 645-648 (2017).
[2] B. G. U. Englert et al., Phys. Rev. Lett. 107, 263003 (2011).
[3] M. Koller et al., Phys. Rev. Lett. 128, 203401 (2022).

17:00 Engineering a Fractional Quantum Hall State of Bosons in an Optical Lattice

Realization of strongly interacting particles under the presence of a magnetic field can lead to novel phases of matter with topological order. Here, we demonstrate adiabatic preparation of the ground state of a two-particle Harper-Hofstadter system under different fluxes with ultracold bosonic 87Rb atoms in an optical lattice. A superimposed running lattice of two Raman beams and a magnetic field gradient are utilized to apply a tunable synthetic gauge field on the atoms. With the single-site resolution provided by our quantum gas microscope, we explore the ground-state fidelity of our protocol over the space of multiple parameters. There are more observables being studied to exhibit phase transition into the fractional quantum Hall state. Our study presents characterization of passage towards topological states in optical-lattice experiments.

Speaker: Mr Sooshin Kim (Harvard University)

17:00 Entangling gates between bosonic qubits in trapped ions

Encoding quantum information in a harmonic oscillator offers a resource efficient method for quantum error correction, compared to the use of multiple two-level systems. The Gottesman-Kitaev-Preskill (GKP) encoding [1] is particularly promising and has recently been realized in both trapped ions [2, 3] and superconducting microwave cavities [4].
State preparation, readout, single qubit rotations and error correction have been achieved in both of these architectures. I will describe work towards logical entangling gates between two GKP qubits prepared in the motional modes of two atomic ions trapped in close proximity. The modes are coupled via the Coulomb interaction, which approximates a beam splitter. Combined with single mode squeezing operations this beam splitter interaction can realize universal entangling gates between the two GKP states [5]. In theoretical work, we have investigated this gate for experimentally realistic parameters and finite energy GKP states. In parallel, we are developing an apparatus for these experiments, including fabrication of a suitable ion trap and design and implementation of optical addressing with tightly focused laser beams.

[1] Daniel Gottesman, Alexei Kitaev and John Preskill, Physical Review A 64, 012310 (2001)

[2] Christa Flühmann et al., Nature 566, 368-372 (2019)

[3] Brennan de Neeve et al., Nature Physics 18, 296-300 (2022)

[4] Philippe Campagne-Ibarcq et al., Nature 584, 368-372 (2020)

[5] Ilan Tzitrin et al., Physical Review A 101, 032315 (2020)

17:00 Experimental realization of classic gates on trapped-ion qubits

The past decade has seen astounding progress in the field of digital quantum computation (QC). Traditionally, QC circuits consist of a set of coherent qubit operations, quantum gates, that are by definition unitary and therefore reversible. Parallel to the familiar use of quantum gates, a new paradigm of quantum information theory is emerging in which hybrid quantum-classic algorithms are proposed for tasks such as quantum simulation, machine learning, and optimization. For example, the simulation of open quantum systems will require an expansion of the current circuit toolbox, to include non-unitary operations. We present an experimental demonstration of a method of realizing controlled non-unitary operations, and use this tool to demonstrate two classic gates with ionic qubits: the OR and NOR operation. The state of one of the two qubits displays the output of the logical operations, and is dependent on the initial state of the two.

We apply the gates using two $^{40}$Ca$^{+}$ ions, trapped in a cryogenic segmented surface trap, as information carriers. The state is encoded in two of the ions' Zeeman sublevels, and is manipulated with optical light-fields. The gates employ engineered resonance through dressed state splitting, based on methods introduced in [1]: Resonant excitation of a two-qubit system transfers information about the two qubit state’s parity to a motional Fock state. Sympathetic cooling of a second co-trapped ion species, $^{80}$Sr$^{+}$, dissipatively removes the motional quanta, making the process non-unitary. We achieve an 87% population fidelity of the OR gate, and an 81% population fidelity of the NOR gate. The main sources of error in our experiments are limits in ground-state cooling of the ion crystal and a non-negligible increase in the motional mode occupation during the experimental sequences.

These experiments are a stepping stone towards an envisioned alternate scheme of quantum error correction (QEC). Conventional proposed QEC schemes rely on classical measurement and feedback to make decisions on whether to apply correction operations or not. Dissipation through engineered resonance prospectively has these decision making processes and correction operations built-in through the conditional state transfer mechanism.

[1] Reiter, F., Sørensen, A.S., Zoller, P. et al. Dissipative quantum error correction and application to quantum sensing with trapped ions. Nat Commun 8, 1822 (2017).

17:00 Experimental setup for trapping and controlling large registers of barium-ion qubits

Trapped-ion systems are amongst the most promising approaches for realizing useful quantum computers and simulators. However, scaling up the qubit register size without compromising performance remains challenging. In the experimental setup presented here we work on realizing large registers of trapped barium-ion qubits.

Barium-ion qubits offer several features favourable for quantum computation experiments. Among these features are optical transitions in the visible range as well as long-lived metastable states which allow for mixed qubit registers that enable novel qubit control schemes like mid-circuit or partial projective measurements and in-sequence cooling. We show an all-fiber Raman system consisting of low-noise 532 nm lasers, standard fiber modulators, and a custom laser-written waveguide beam delivery system capable of single-ion addressing. We confine the ions in a segmented monolithic 3D microfabricated trap [1] that allows for advanced trapping potential control while simultaneously providing a low heating rate.

Odd barium isotopes additionally offer a range of magnetically insensitive “clock”-states in the ground and metastable states. Amongst them, the radioactive isotope $^{133}$Ba$^+$, with a nuclear spin of $I = 1/2$, has the simplest level structure [2]. While its lifetime of 10.51 years is not problematic for its use as qubit, radiation safety considerations require sample sizes of only a few micrograms, too little for conventional oven loading schemes. Here we present our work towards fabricating BaCl$_2$ targets that are suitable for ablation loading.

[1] P. See, et al., Journal of Microelectromechanical Systems 22, (2013)
[2] J. E. Christensen, et al., npj Quantum Information 6, (2020)

17:00 Exploring topology in synthetic quantum Hall systems using atomic dysprosium

Topological quantum states are associated with integer invariants and are thus protected from continuous small deformations of the system. Topological invariants ensure the robustness of various phenomena, e.g. the quantized Hall conductance in two-dimensional electron gases subjected to a magnetic field, and are promising tools in different fields of physics, such as quantum computation. Phases characterized with non-trivial topological invariants have been widely studied in the context of the integer and fractional quantum Hall effects and of topological insulators, both theoretically and experimentally.

Recently, the concept of synthetic dimension has attracted attention as it allows extending current studies to more exotic geometries. It relies on internal degrees of freedom to simulate an extra dimension, with an additional flexibility on its properties compared to a real physical dimension.

In this poster, I will present some recent experimental works on quantum Hall systems using ultracold samples of atomic dysprosium. We benefit from the large total angular momentum J=8 of dysprosium atoms in their electronic ground state to simulate a synthetic dimension, with 2J+1=17 discrete positions. In a previous work, using optical Raman transitions coupling neighboring Zeeman sublevels of the electronic ground state, we showed that a Hall ribbon with sharp edges can be engineered.

We now report the use of this internal degree of freedom as a discretized dimension with periodic boundary conditions, used to prepare the equivalent of a Hall cylinder. In this geometry, the threading of a quantum of magnetic flux through the hole of the cylinder induces a quantized particle transport along the inifinite dimension, associated to the 1st Chern number.
Pushing the versatility of this approach forward, we also encode two synthetic dimensions in the total angular momentum of each atom, that we couple to two real physical dimensions. This effectively simulates a four-dimensional quantum Hall system with one cyclic dimension, one finite dimension with edges and two infinite dimensions. The dimensionality strongly affects the underlying physics: the topology of four-dimensional Hall systems is characterized by the 2nd Chern number which corresponds to a quantized non-linear response.

17:00 Generating and detecting topological phases with higher Chern number

Topological phases with broken time-reversal symmetry and Chern number |C|>=2 are of fundamental interest, but it remains unclear how to engineer the desired topological Hamiltonian within the paradigm of spin-orbit-coupled particles hopping only between nearest neighbours of a static lattice. We show that phases with higher Chern number arise when the spin-orbit coupling satisfies a combination of spin and spatial rotation symmetries. We leverage this result both to construct minimal two-band tight binding Hamiltonians that exhibit |C|=2,3 phases, and to show that the Chern number of one of the energy bands can be inferred from the particle spin polarization at the high-symmetry crystal momenta in the Brillouin zone. Using these insights, we provide a detailed experimental scheme for the specific realization of a time-reversal-breaking topological phase with |C|=2 for ultracold atomic gases on a triangular lattice subject to spin-orbit coupling. The Chern number can be directly measured using Zeeman spectroscopy; for fermions the spin amplitudes can be measured directly via time of flight, while for bosons this is preceded by a short Bloch oscillation. Our results provide a pathway to the realization and detection of novel topological phases with higher Chern number in ultracold atomic gases.

17:00 High-precision measurements of atomic structure in Lead and other multi-valence atomic systems

We have undertaken a series of measurements of atomic properties of group III and IV systems to test ongoing ab initio atomic structure calculations. These multi-valence systems have relevance to tests of symmetry violation and other fundamental physics searches. Prior work involved measurements of polarizability, isotope shifts, and hyperfine structure in various excited states of the three-valence thallium and indium systems.

Recently, we have focused on the four-valence Pb system where significantly improved atomic structure calculations [1] have been completed for an atomic system in which two different precise atomic parity nonconservation experiments were performed two decades ago. Unlike alkali systems, relatively few atomic benchmark measurements exist in Pb at a level of accuracy necessary to test and guide refinement of the theory. In 2019, we completed the first measurement of the forbidden Pb (6s$^{2}$6p$^{2}$) $^3$P$_0$ - $^3$P$_{2}$ E2 transition amplitude at 939 nm, finding excellent agreement with the ab initio value computed by the Safronova group at the 1% level of accuracy. The experimental method employed the same high-precision polarimetry technique used to measure parity non-conserving optical rotation. This technique, which uses crossed polarizers and a Faraday modulation / lock-in detection technique, yields $\mu$Radian precision, allowing measurement of very weak atomic transitions via detection of milliradian-sized Faraday rotation using small DC magneticfields applied to the sample.

We are currently pursuing several new Pb atomic structure measurements using this same Faraday polarimetry method. These include measurements of transition isotope shifts and hyperfine splittings in these forbidden transitions using isotopically-enriched vapor cells, as well as measurements of electric dipole amplitudes for transitions originating in thermally-excited levels with populations of order 10$^{-5}$ of the ground-state population.

Additionally we plan to measure, for the first time, excited-state polarizabilities in Pb, using the same atomic beam apparatus and high-voltage field-plate system used in our lab for prior measurements in indium and thallium. Here, a molybdenum crucible containing 300 g of lead is heated to above 1000 $^\circ$C to create a dense, collimated atomic beam. The sensitive Faraday polarimetry method will be used to perform transverse spectroscopy in the presence of this beam and static electric fields up to 20 kV/cm will create Stark shifts in the 368 nm (6s$^{2}$6p$^{2}$) $^3$P$_1$ - $(6s^{2}6p7s)^3P_{0}$ E1 transition. The predicted Stark shift is roughly half the expected Doppler-narrowed line width, and we expect to see Faraday rotation signals of order 100 $\mu$Radians, which should be easily measurable using our polarimetry technique, providing a new, exacting test of the atomic theory predictions.

Current results will be presented.

[1] D.L. Maser, Eli Hoenig, B.-Y. Wang, P.M. Rupasinghe, S.G. Porsev, M.S. Safronova, and P.K. Majumder, Phys. Rev A 100, 052506 (2019).

17:00 Interactions and ultracold scattering of Cr with Yb

We investigate the scattering of a high-spin spherical atom Cr ($^7$S) with a closed shell atom Yb ($^1$S). We evaluate the spin-spin interaction arising from the multiple unpaired electrons from the Cr atom perturbed by the Yb atom, and show this provides a substantial coupling. We perform calculations of the magnetic Feshbach resonances this causes, and show are guaranteed to exist at low magnetic fields (below $\sim250$ G) with experimentally useful widths, regardless of the scattering length. This system has advantages over other similar systems such as alkali-metal+alkaline-earth systems – where the resonances are extremely narrow – and systems involving non-s-state atoms such as Er or Dy – which are extremely hard to make accurate microscopic models of. Applications of this system could include a starting point to form novel high-spin molecules or controlling interactions in a mixed gas of dipolar and non-dipolar atoms.

17:00 Interference of Bose-Einstein condensates with the Lee-Huang-Yang correction: a theoretical scheme

We propose a theoretical scheme to study the Lee-Huang-Yang (LHY) quantum correction on the interference of two expanding Bose-Einstein condensates (BEC). The key is to consider a long-term expanding condensate whose wave function mimics the dynamic Gaussian wave. This enables to solve analytically the wave function at an earlier time when the LHY correction is active. Based on the GPE approach, we then perform the simulations for the interference, and a good agreement with the theory has been achieved. Our results suggest that interference might be a good candidate to identify the LHY correction in a BEC system.

17:00 Intra-Cavity Frequency-Doubled VECSEL System for Narrow Linewidth Rydberg EIT Spectroscopy

Vertical external-cavity surface-emitting lasers (VECSELs) augmented by intracavity nonlinear optical frequency conversion have emerged as an attractive light source of ultraviolet to visible light for demanding scientific applications, relative to other laser technologies. They offer high power, low phase noise, wide frequency tunability, and excellent beam quality
in a simple and inexpensive system architecture. Here, we characterize the frequency stability of an intra-cavity frequency-doubled VECSEL with 690 mW of output power at 475 nm using the delayed self-heterodyne technique and direct comparison with a commercial external-cavity diode laser (ECDL). We measure the fundamental’s Lorentzian linewidth to be 2𝜋 × 5.3(2) kHz, and the total linewidth to be 2𝜋 × 23(2) kHz. In addition, we perform Rydberg-state spectroscopy
via electromagnetically induced transparency (EIT), observing narrow 3.5 MHz full-width half maximum EIT. By doing so, we demonstrate that intra-cavity frequency-doubled VECSELs can perform precision spectroscopy at the MHz level, and are a promising tool for contemporary, and future, quantum technologies

17:00 Manipulating and measuring states of an optomechanical resonator in the quantum regime

Macroscopic mechanical devices in the quantum regime can play a key role in quantum communication, quantum sensing and fundamental tests of quantum mechanics. We use a fiber cavity filled with superfluid $^4$He of mass ~ 1 ng as our mechanical resonator. Leveraging single photon counting techniques, we manipulate and probe the motional state of a superfluid $^4$He resonator. The arrival times of Stokes and anti-Stokes photons are used to measure the resonator’s phonon coherences. We demonstrate the coherences of a thermal state near the motional ground state, a non-classical photon-phonon squeezed state, and a high amplitude coherent state in this superfluid $^4$He resonator. These measurements pave the avenue of realizing a non-classical state in a milligram resonator in future experiments.

17:00 Measurements of $n$p - 2s transitions in the hydrogen atom

Precision experiments in the hydrogen atom have a long tradition and extensive studies of transitions between low lying $n\leq12$ states were carried out [1-6]. These measurements can be used to determine values of the Rydberg constant and the proton charge radius. We present a new experimental approach to perform measurements of transition frequencies between the metastable 2s $^{2}$S$_{1/2} (F = 0,1)$ state of H and highly excited $n$p-Rydberg states with principal quantum number $n \geq 23$.
We generate the hydrogen atoms by dissociating H$_2$ in a dielectric barrier discharge located at the orifice of a pulsed cryogenic valve. The hydrogen atoms are entrained in the supersonic expansion of H$_2$. The atoms are photoexcited to a specific hyperfine level of the metastable 2s $^{2}$S$_{1/2}$ state by a home-built frequency-tripled Fourier-transform-limited pulsed titanium-sapphire laser (pulse length 40 ns). They enter a magnetically shielded region in which transitions to $n$p Rydberg states are induced by a narrow-band frequency-doubled continuous-wave titanium-sapphire laser, which is phase locked to an optically stabilized frequency comb and referenced over a fiber network to a SI traceable primary frequency standard [7]. The highly excited Rydberg states are detected by pulsed-field ionization. We will report progress on our efforts to minimize uncertainties from stray electric fields and Doppler shifts and to obtain spectral lines with a FWHM below 10 MHz.
This work was supported by the Swiss National Science Foundation through the Sinergia-Program (Grant No. CRSII5-183579) and Grant No. 200020B-200478.

[1] J. C. Garreau $\textit{et al.}$, J. Phys. France $\textbf{51}$, 2293 (1990).
[2] C. G. Parthey $\textit{et al.}$, Phys. Rev. Lett. $\textbf{107}$, 203001 (2011).
[3] A. Beyer $\textit{et al.}$, Science $\textbf{358}$, 79 (2017).
[4] H. Fleurbaey $\textit{et al.}$, Phys. Rev. Lett. $\textbf{120}$, 183001 (2018).
[5] N. Bezginov $\textit{et al.}$, Science $\textbf{365}$, 1007 (2019).
[6] A. Grinin $\textit{et al.}$, Science $\textbf{370}$, 1061 (2020).
[7] D. Husmann $\textit{et al.}$, Optics Express $\textbf{29}$,24592 (2021).

17:00 Measuring the Chern number with weakly interacting spin-orbit-coupled Bose gases in optical lattices

The quantification of topological invariants for tight-binding Hamiltonians with certain crystalline point group symmetries is well-studied, and in particular, the Chern number can be expressed in terms of the eigenvalues of the symmetry operator at the high-symmetry points of the Brillouin zone [1]. In recent years, it has become possible to utilize this relation in cold atom experiments to measure the Chern number by loading spinor BECs with spin-orbit coupling onto 2D optical lattices (e.g. Ref. [2]). Spin polarization measurements are used to quantify the topological invariant, although so far it has been limited to Chern number 1. A recent experimental proposal based on Chern insulators with additional spin-space symmetries has paved the way for extracting higher Chern number with better resolution by performing polarization measurements only at those high-symmetry points for an ideal BEC [3]. In this work, we go beyond the assumption that the BEC is non-interacting and study the effects of interactions that are weak enough not to destroy the condensation but can still be comparable or even stronger than the band gaps of the spin-orbit coupling Hamiltonian. Our framework is based on a mean-field treatment including fluctuations. Aside from quantifying the deviations in Chern number measurements from the non-interacting limit, we are able to investigate other interesting effects arising from the competition between the interactions, spin-orbit coupling, and the optical lattice potential under realistic experimental conditions.

Acknowledgments
This work was supported by the Alberta Major Innovation Fund.

References
[1] C. Fang, M. J. Gilbert, and B. A. Bernevig, Phys. Rev. B 86, 115112 (2012)
[2] Z. Wu, L. Zhang, W. Sun, X.-T. Xu, B.-Z. Wang, S.-C. Ji, Y. Deng, S. Chen, X.-J. Liu, and J.-W. Pan, Science 354, 83 (2016).
[3] A. Alase and D. L. Feder, Phys. Rev. A 103, 053305 (2021)

17:00 Measuring the n=2 triplet P fine structure of atomic helium using Frequency-Offset Separated Oscillatory Fields (FOSOF)

The n=2 triplet P fine structure of atomic helium is being measured using microwave transitions.
The method [1] of Frequency-Offset Separated Oscillatory Fields (FOSOF) is used to perform
the measurements. The measurement of the J=1-to-J=2 interval has been completed [2], with a
measurement uncertainty of only 25 Hz. The measurement of the 29.6-GHz J=0-to-J=1 interval
is now being performed. These measurements, together with sufficiently precise theoretical
predictions for the intervals (see [3] for the current state-of-the-art calculations) can be used to
determine a value for the fine-structure constant and to test for possible physics beyond the
standard model.

[1] A. C. Vutha and E. A. Hessels, Phys. Rev. A 92, 052504 (2015).
[2] K. Kato, T. D. G. Skinner and E. A. Hessels, Phys. Rev. Lett. 121, 143002 (2018).
[3] K. Pachucki and V. A. Yerokhin, Phys. Rev. Lett. 104, 070403 (2010).

17:00 Multi-loop atomic Sagnac interferometry

Inertial sensors based on matter-wave interference show great potential for navigation, geodesy, or fundamental physics. Similar to the Sagnac effect, their sensitivity to rotations increases with the space-time area enclosed by the interferometer. In the case of light interferometers, the latter can be enlarged by forming multiple fibre loops. However, the equivalent for matter-wave interferometers remains an experimental challenge. This contribution presents a concept for a multi-loop atom interferometer with a scalable area formed by multiple light pulses. It exploits ultra-cold atomic ensembles combined with symmetric beam splitting and a relaunch mechanism. Due to its scalability it offers the perspective of reaching unprecedented sensitivities for rotations in compact sensor head setups.

Funded/supported by the DFG, ID 274200144 SFB 1227 DQ-mat within B07 & B09, & ID 434617780–SFB 1464 TerraQ within A01, A02 & A03 & EXC-2123 QuantumFrontiers, ID 390837967; by the DLR by the BMWi under DLR 50WM1952 & 50WM1955 (QUANTUS-V-Fallturm), 50WP1700 (BECCAL), 50RK1957 (QGyro), DLR 50NA2106 (QGyro+) & the VDI by the BMBF under VDI 13N14838 (TAIOL); by the BMBF under 13N14875 and from “Niedersächsisches Vorab” for the initial funding of the DLR-SI Institute and through QUANOMET (QT3).

17:00 NASA’s Cold Atom Laboratory: a multi-user facility for quantum gas research on the International Space Station

NASA’s Cold Atom Laboratory (CAL) was launched to the International Space Station in 2018, where it has been conducting quantum experiments in microgravity ever since. CAL is a multi-user instrument designed to be fully operated remotely, with the possibility of astronaut-led hardware upgrades and replacements. Scientists have performed investigations ranging from BECs in bubble shaped geometries to extreme cooling protocols, all while commissioning efforts are under way to demonstrate atom interferometry and dual species BECs in space.

17:00 Noisy Atomic Magnetometry in Real Time

Continuously monitored atomic spin-ensembles allow, in principle, for real-time sensing of external magnetic fields beyond classical limits. Within the Linear-Gaussian regime, thanks to the phenomenon of measurement-induced spin-squeezing, they attain a quantum-enhanced scaling of sensitivity both as a function of time, t, and the number of atoms involved, N. In our work, we rigorously study how such conclusions based on Kalman filtering methods change when inevitable imperfections are taken into account: in the form of collective noise, as well as stochastic fluctuations of the field in time. We prove that even an infinitesimal amount of noise disallows the error to be arbitrarily diminished by simply increasing N, and forces it to eventually follow a classical-like behavior in t. However, we also demonstrate that, “thanks” to the presence of noise, in most regimes the model based on a homodyne-like continuous measurement actually achieves the ultimate sensitivity allowed by the decoherence, yielding then the optimal quantum-enhancement. We are able to do so by constructing a noise-induced lower bound on the error that stems from a general method of classically simulating a noisy quantum evolution, during which the stochastic parameter to be estimated—here, the magnetic field—is encoded. The method naturally extends to schemes beyond the linear-Gaussian regime, in particular, also to ones involving feedback or active control.

17:00 Nonequilibrium dynamics in a quenched ferromagnetic spinor Bose-Einstein condensate

In this poster, we will present recent experiments on a quenched ferromagnetic spinor BECs. In the first part, we present the observation of spin-momentum correlated matter-wave jets from spinor BECs [1]. Preparing a quasi-two-dimensional condensate in the $m_F=0$ state, we quench the quadratic Zeeman energy to -2 kHz. Transversely propagating atomic beams in the $m_F=1$ and $m_F=-1$ state ($m_F =0$ state) are generated due to the superradiant collision process. Investigating angular correlation for each spin state, we reveal the strong correlation between spin and momentum, which suggests the possibility of being Einstein-Podolsky-Rosen (EPR) state. In the second part, we investigate the long-time relaxation dynamics after the quench [2,3]. Generated spin pairs form magnetic domains and are merged to display coarsening dynamics. We investigate correlation functions of the magnetization and observe the functions at different time collapse to a single function. Our result shows a good agreement with numerical simulation.
[1] K. Kim, J. Hur, S. Huh, S. Choi, and J.-Y. Choi, Phys. Rev. Lett. 127, 043401 (2021)
[2] L. A. Williamson and P. B. Blakie., Phys. Rev. Lett. 116, 025301 (2016)
[3] J. Hofmann, S. S. Natu, and S. Das Sarma, Phys. Rev. Lett. 113, 095702 (2014).

17:00 Observation of a continuous time crystal

Time crystals are classified as discrete or continuous depending on whether they spontaneously break discrete or continuous time translation symmetry. While discrete time crystals have been extensively studied in periodically driven systems since their recent discovery, the experimental realisation of a continuous time crystal [1,2] is still pending. We report the observation of a limit cycle phase in a continuously pumped dissipative atom-cavity system [3], which is characterized by emergent oscillations in the intracavity photon number. We observe that the phase of this oscillation is random for different realisations, and hence this dynamical manybody state breaks continuous time translation symmetry spontaneously. The observed robustness of the limit cycles against temporal perturbations confirms the realisation of a continuous time crystal.

References

[1] F. Piazza and H. Ritsch,
Self-Ordered Limit Cycles, Chaos, and Phase Slippage with a Superfluid
inside an Optical Resonator,
PRL, 115, 163601 (2015).
[2] H. Keßler, J. G. Cosme, M. Hemmerling, L. Mathey, and A. Hemmerich,
Emergent limit cycles and time crystal dynamics in an atom-cavity system,
PRA, 99(5), 053605 (2019).
[3] P. Kongkhambut, J. Skulte, L. Mathey, J. G. Cosme, A. Hemmerich, and H.
Keßler, Observation of a continuous time crystal,
arXiv:2202.06980 (2022).

17:00 Observation of interaction-driven delocalization of the Anderson insulator in synthetic dimensions

The quantum kicked rotor is a paradigm system to study classical and quantum chaos. When viewed in momentum space, it is equivalent to the Anderson model of transport in the presence of disorder, featuring dynamical localization in the synthetic momentum space. We report the observation of interaction-driven delocalization in d-dimensional (d=1-4) Anderson models in the synthetic momentum space. Higher dimensions are generated by amplitude modulating the kick pulses of the quantum kicked rotor, and interactions are controlled via the transverse confinement of the 1D tubes. We show that interaction destroys dynamical localization for d=1-4, and the dynamics of the system becomes sub-diffusive. We also observed the onset of delocalization to start earlier with stronger interaction, modulation, and kick. Compared to earlier experimental studies in position space, our approach addresses interaction-driven transport in the Anderson model in great than 1 dimension and with infinitely-long range interactions realized in momentum space.

Speaker: Jun Hui See Toh (University of Washington, Seattle)

17:00 Optical clocks with trapped $^{40}$Ca$^{+}$ and $^{27}$Al$^{+}$ ions

The search for more precise and accurate frequency standards has played a key role in the development of basic science, precision measurements and technical applications. Nowadays, optical clocks with trapped ions are achieving uncertainties in the low 10$^{-18}$ range and below. One of our group’s focuses is centered on the implementation of optical clocks with trapped $^{40}$Ca$^{+}$ and $^{27}$Al$^{+}$.

Since its first measurement in 2009 by our group, the absolute frequency of the $4s$ $ ^{2}S_{1/2}\leftrightarrow 3d$ $^{2}D_{5/2}$ $^{40}Ca^{+}$ clock transition has been reported 4 more times. However, the first two of these published results (between 2009 and 2012) disagree with the latter two (between 2013 and 2017). We present the results of a new campaign to measure the absolute frequency of $^{40}Ca^{+}$ clock transition with respect to the coordinated universal time UTC at PTB by means of a GNSS link using the Precise Point Positioning (PPP) technique. After evaluation of the systematic shifts, the transition frequency is measured to be (411 042 129 776 401.3±0.6) Hz with a fractional uncertainty of 1.4 × 10$^{-15}$.

To investigate the optical transitions on the $^{27}$Al$^{+}$, we implement Quantum Logic Spectroscopy (QLS). QLS consists of the combined implementation of an auxiliary “logic” ion, which is stored together with a “spectroscopy” ion. The “logic” ion is used to cool down the initially hot “spectroscopy” ion via their Coulomb interaction and additionally allows the preparation and detection of the internal state of the “spectroscopy” ion. We performed QLS for a measurement of the $^{1}\mathrm{S}_{0}\leftrightarrow~^{3}\mathrm{P}_{1}$ intercombination transition in $^{27}$Al$^{+}$. Ramsey spectroscopy is used for probing the transition in $^{27}$Al$^{+}$ and the $4s$ $ ^{2}S_{1/2}\leftrightarrow 3d$ $^{2}D_{5/2}$ clock transition in $^{40}Ca^{+}$ in interleaved measurements. By using the precisely measured frequency of the clock transition in $^{40}Ca^{+}$ as a frequency reference we determine the frequency of the intercombination line to be 1 122 842 857 334 736(93) Hz and the Landé g-factor of the excited state to be 0.428132(2) [1]. We have also probed the $^{1}\mathrm{S}_{0}\leftrightarrow~^{3}\mathrm{P}_{0}$ $^{27}$Al$^{+}$ clock transition with a probe-time-limited width of 1 kHz. Efforts to obtain spectrally narrower lines are mostly hampered by the formation of molecular ions by reaction of the Al+ with H2 background gas molecules. Molecular ion formation limits the time that we can uninterruptedly probe the clock transition to about 15 minutes, which in combination with long Al$^{+}$ reloading times, prevent us from investigating the clock transition more thoroughly.

Our latest project focuses on the development of three different experimental techniques to investigate trapped-ion kinetics due to background-gas collisions. Background gas collisions can perturb the frequency of atomic clocks. The energy imparted during collision events affects the motional state distribution, which consequently has an effect on the time-dilation, also known as second-order Doppler shift. In Additional to this shift, any interaction during the collision can perturb the phase of the atomic superposition. The three techniques together detect a range in energy due to collisions spanning 7 orders of magnitude. The first technique uses a composite sequence of optical transitions in Ca$^{+}$ to accurately transfer information about its motional state, allowing the detection of collisions that impart a kinetic energy between 10$^{-3}$ K to 10$^{-1}$ K. The second technique is based on the detection of collisions that cause a reordering of a mixed-species ion pair and covers a range from 10$^{-1}$ K to 10 K. The third technique is based on the characterization of the re-cooling dynamics of a single calcium ion after a collision and covers a range from 10 K to 10$^{4}$ K. The experimental characterization of trapped-ion kinetics due to background-gas collisions through such a broad range opens the door to a deeper understanding of the background-gas composition and its effect on trapped ion experiments.

[1] M Guggemos et al. “Frequency measurement of the 1$^{1}\mathrm{S}_{0},F=5/2\leftrightarrow~^{3}\mathrm{P}_{1},F=7/2$ transition of $^{27}$Al$^{+}$ via quantum logic spectroscopy with $^{40}$Ca$^{+}$”. In: New Journal of Physics 21.10 (2019), p. 103003.

17:00 Optical switching of an atomic Bragg mirror around a nanofiber

In the recent years, the use of nanoscale waveguides providing tight transverse confinement of light has been pushed forward in the waveguide-QED field as a mean to enhance atom-photon interactions for large number of atoms. On our experiment, we use a two-color dipole trap scheme to interface cold Cesium atoms with the evanescent field of a tapered optical nanofiber. By tuning the properties of the dipole trap, we arrange the atoms in a 1D lattice geometry with controllable distance between them.

In the past, we used this platform to demonstrate an all-fibered optical memory at the single-photon level using dynamical EIT [1]. We also investigated collective behaviors in such 1D chains of trapped atoms. We demonstrated up to 80\% Bragg reflection with as low as 2000 atoms when carefully tuning the interatomic distance [2]. More recently, we heralded the creation of a single collective excitation in the atomic chain, which was subsequently stored and retrieved as a single photon in the guided mode of the nanofiber [3]. We also theoretically studied the collective dynamics of cavity-QED-like atomic arrangements in both markovian and non-markovian regimes [4].

A strong motivation is also to reach quantum non-linearity at few-photon levels. In this context, controlling the propagation of a single photon with powers at the single-photon levels in cavity-free platforms has been studied in few systems [5], and still remains an important milestone for the community. Here, we report on guided optical switching and routing of single-photon level coherent fields using an atomic Bragg mirror controlled by very low energy fields. Focusing first on the regular three-level setup, we switch the reflection and the transmission paths of a Bragg mirror using electromagnetically-induced transparency (EIT). The control beam is guided and contains around few thousand photons. In order to push this number even lower, we employ a four-level scheme consisting of the previous scheme to which we add an additional level coupled with the metastable state by a switch field. We demonstrate optical switching with a switch field at the few-tens of photons level, thus reducing by one to two order of magnitude the number of photons needed. Routing, or controlled directionnality of the probe photon, is also achieved using the same four-level scheme with a switch field at at the few hundred photons level.

[1] B. Gouraud, D. Maxein, A. Nicolas, O. Morin, and J. Laurat, “Demonstration of a memory for tightly guided light in an optical nanofiber,” Phys. Rev. Lett. 114, 180503 (2015).

[2] N. V. Corzo, B. Gouraud, A. Chandra, A. Goban, A. Sheremet, D. Kupriyanov, and J. Laurat, “Large bragg reflection from one-dimensional chains of trapped atoms near a nanoscale waveguide,” Phys. Rev. Lett. 117, 133603 (2016).

[3] N. V. Corzo, J. Raskop, A. Chandra, A. S. Sheremet, B. Gouraud, and J. Laurat, “Waveguide-coupled single collective excitation of atomic arrays,” Nature 566, 359–362 (2019)

[4] V. A. Pivovarov, L. V. Gerasimov, J. Berroir, T. Ray, J. Laurat, A. Urvoy, and D. V. Kupriyanov, “Single collective excitation of an atomic array trapped along a waveguide : a study of cooperative emission for different atomic chain configurations,” Phys. Rev. A 103, 043716 (2021).

[5] M. Bajcsy, S. Hofferberth, V. Balic, T. Peyronel, M. Hafezi, A. S. Zibrov, V. Vuletic, and M. D. Lukin, "Efficient all-optical switching using slow light within a hollow fiber", Phys. Rev. Lett. 102, 203902 (2009)

17:00 Parameter optimization for laser slowing and magneto-optical trapping of MgF molecules via motion simulation

A magneto-optical trap (MOT) is the first step to take various atoms and molecules to the ultracold temperature. For molecules, because of their complex energy structure, there are too many parameters to be adjusted in the MOT and the preceding laser slowing stage. It is difficult to experimentally optimize all the parameters one by one. Motion simulation of particle can provide the optimized parameters more efficiently, and also can give us the motional trace to check if parameters are valid for MOT and laser slowing.

We optimize the parameters for MOT and laser slowing of Magnesium monofluoride (MgF) via motion simulation, to maximize the capture velocity ($v_c$) and the ratio of trapped molecules to the total molecules from a cold buffer-gas beam source ($R_{trap}$). We simulate the motion of MgF in two stages, MOT region and laser slowing region, using rate equation model. In the MOT region, we optimized various parameters of lasers and magnetic field to maximize $v_c$, using Bayesian optimization method. Using the optimized experimental parameters, we set a capture condition of initial positions and velocities which determines if molecules are trapped or not, when they enter the stage. In laser slowing stage, we optimize the parameters of slowing lasers to maximize $R_{trap}$ using the capture condition of the MOT. In the poster, we further discuss the overall structure, initial conditions and optimization result of the simulation.

17:00 Pattern formation in tilted optical lattices

Driving a many-body system out of equilibrium induces phenomena such as the emergence and decay of transient states, which can manifest itself as pattern and domain formation. The understanding of these phenomena expands the scope of established thermodynamics into the out-of-equilibrium domain. We report our theoretical and experimental study on the out-of-equilibrium dynamics of a bosonic lattice model subjected to a strong dc field, realized as ultracold atoms in a strongly tilted optical lattice. We observe the emergence of pronounced density-wave patterns, which spontaneously break the underlying lattice symmetry. The experimental observation utilizes a single-shot imaging technique with two-dimensional single-site resolution in three-dimensional systems, which also resolves the domain structure. Our study suggests that the short-time dynamics arises from resonant pair tunneling processes within an effective description of the tilted Hubbard model. More broadly, we establish the far out-of-equilibrium regime of lattice models subjected to a strong dc field, as an exemplary and paradigmatic scenario for transient pattern formation.

H. P. Zahn, V. P. Singh, M. N. Kosch, L. Asteria, L. Freystatzky, K. Sengstock, L. Mathey, and C. Weitenberg, Phys. Rev. X 12, 021014 (2022)

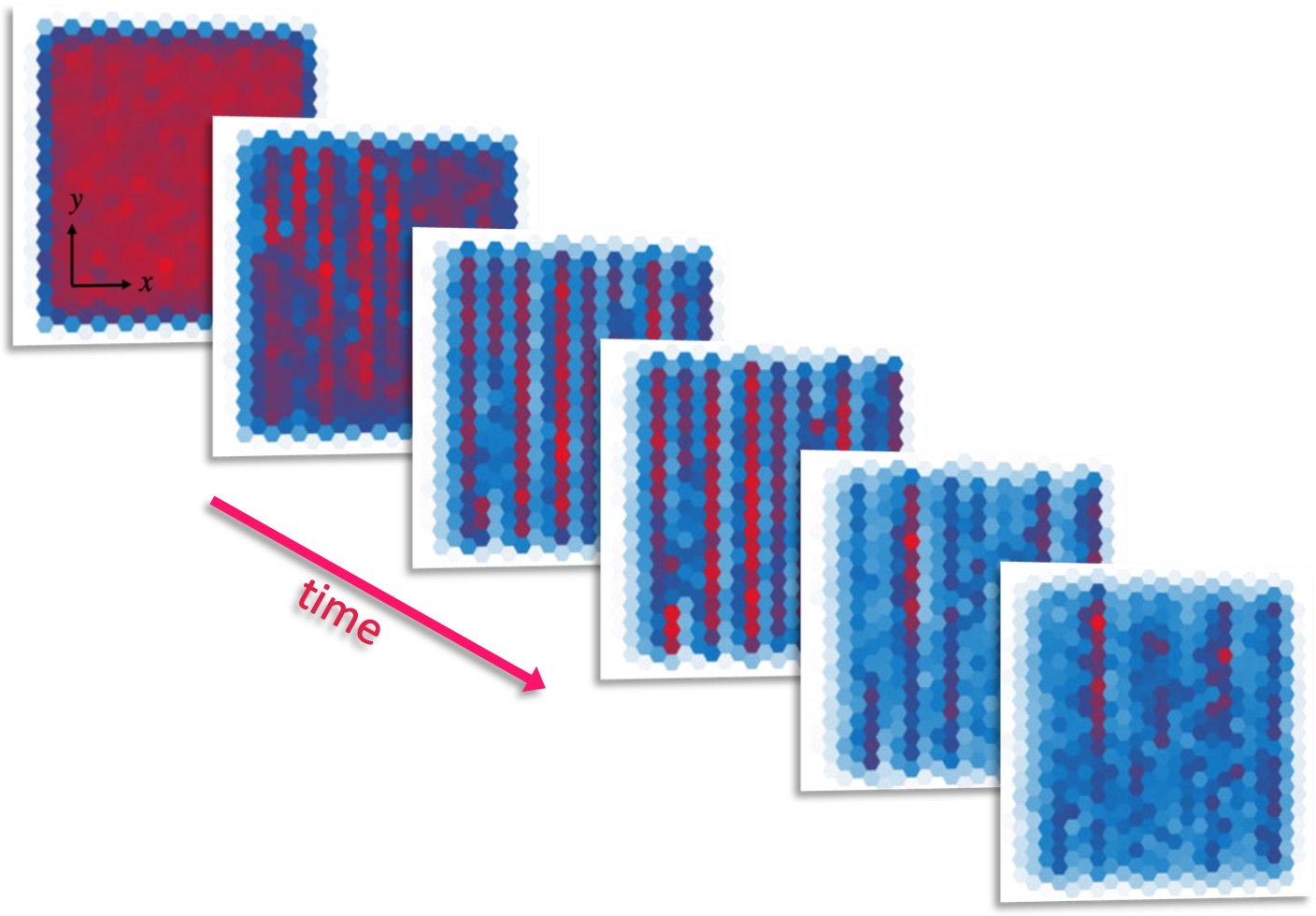
17:00 Perturbative calculation of the energy of an impurity immersed in a spin-1/2 Fermi superfluid in the Random-Phase Approximation

In order to investigate the low-energy physics of a system composed of an impurity immersed in a many-body medium, one may study the properties of the quasiparticle formed by the impurity dressed by excitations of the surrounding medium : the so-called polaron. This idea was first introduced in solid-state physics by Landau and Pekar in the 1950’s to study the coupling of electrons to a crystalline lattice. Decades after these first theoretical studies, the development of the field of ultracold atoms provided a variety of experimental setups for the study of polaron physics : an impurity in a weakly interacting Bose-Einstein Condensate (BEC) forms a Bose polaron, whereas a Fermi polaron is obtained when the surrounding medium is a Fermi sea. By choosing the surrounding medium to be a 2-component Fermi superfluid, we can interpolate between these two types of physics along the BEC-BCS crossover.
We present a calculation of the energy of an impurity weakly coupled to a spin-1/2 fermionic superfluid based on Random-Phase Approximation. We show that it is necessary to go beyond mean-field BCS theory in order to have a proper description of the excitations of the many-body background, allowing us to cure the divergences caused by three-body effects. RPA allows us to describe the excitations of the system along the BEC-BCS crossover and to regularize the energy of the impurity. These effects should be experimentally observable, for example in the case of a small BEC immersed in a Fermi superfluid, through a measurement of the frequency shift of the oscillations of the impurity in an external potential.

17:00 Preparation of the Spin-Mott State: A Spinful Mott Insulator of Repulsively Bound Pairs

We observe and study a special ground state of bosons with two spin states in an optical lattice: the spin-Mott insulator, a state that consists of bound pairs that is insulating for both spin and charge transport. Because of the pairing gap created by the interaction anisotropy, it can be prepared with low entropy and can serve as a starting point for adiabatic state preparation. We find that the stability of the spin-Mott state depends on the pairing energy and observe two qualitatively different decay regimes.

17:00 Probing open- and closed-channel p-wave Feshbach resonances

We study a $p$-wave Feshbach resonance in potassium-40 with a combination of spectroscopic binding energy measurements, coupled-channels calculations, and a two-channel model [1]. Using both resonant association and spin-flip association, the binding energy of bound and quasi-bound dimers is measured across a five-gauss range. Our scattering model incorporates the ramping closed-channel state, weak dipole-dipole interactions, and a low-lying $p$-wave shape resonance in the open channel. The open-channel resonance affects low energy scattering and creates nonlinearity in the binding energy near threshold, which resolves an open question [2]. We explain why in the low-energy limit a divergent contribution to the scattering volume from dipole-dipole interactions violates the $p$-wave threshold law, and how we isolate the contribution of the short-range potentials to scattering. Our improved understanding of $p$-wave scattering near this resonance enables quantitative testing of predictions for low-dimensional odd-wave gases, and lays a basis for future few- and many-body $p$-wave experiments.
[1] D. J. M. Ahmed-Braun, K. G. Jackson, S. Smale, C. J. Dale, B. A. Olsen, S. J. J. M. F. Kokkelmans, P. S. Julienne, J. H. Thywissen, Probing open- and closed-channel $p$-wave resonances, Phys. Rev. Research 3, 033269 (2021).
[2] J. P. Gaebler, J. T. Stewart, J. L. Bohn, and D. S. Jin, $p$-wave Feshbach molecules, Phys. Rev. Lett. 98, 200403 (2007).

17:00 Progress towards direct laser cooling and trapping of CaH molecules

The past decade has seen tremendous progress in the field of direct laser cooling and trapping of molecules, extending to new candidate platforms for quantum computing, quantum simulation, precision measurement and metrology. Here we present our progress towards laser cooling and trapping of CaH molecules. We demonstrate experimental results on transverse Sisyphus cooling of a cold beam of CaH molecules. We obtain good agreement with the optical Bloch equations and Monte Carlo simulations, and establish that a high scattering rate (~10^6 photons/s) is achievable for this molecule. Next, we present our characterization of molecular predissociation and discuss potential dissociation pathways for the creation of atomic hydrogen from CaH. Looking toward the future, we describe our plans to perform longitudinal white-light slowing and 3D magneto-optical trapping with the application of the first two vibrational repumps. This work sets the stage for a trapped, dilute cloud of ultracold hydrogen, which could further improve on the current limits in hydrogen spectroscopy.

17:00 Quantum Control of Motional States in Mixed-Species Trapped-Ion Crystals

The spectral separation between resonant transitions of different ion species offers mutual isolation that can be advantageous for scaling trapped ion quantum computing systems, and numerous groups are now performing experiments with mixed-species crystals of trapped ions. In our group at NIST, trapped $^9$Be$^+$ and $^{24/25}$Mg$^+$ ions in a linear RF trap have been utilized to demonstrate sympathetic cooling, logic gates, gate teleportation, quantum-logic spectroscopy, and high-fidelity indirect readout. Here we discuss two further experiments on quantum control of mixed-species trapped-ion chains.

We modify electromagnetically-induced-transparency (EIT) cooling techniques to accommodate the hyperfine structure of $^{25}$Mg$^+$. EIT cooling, as originally conceived, is a broad-bandwidth, rapid, sub-Doppler cooling method suitable for three-level $\Lambda$ systems. EIT cooling also requires less laser power than far-detuned Raman sideband cooling. While the hyperfine levels of $^{25}$Mg$^+$ are suitable for the implementation of qubits, the presence of more than two ground levels (in contrast to $^{24}$Mg$^+$) requires modification of the original EIT cooling approach. We present experimental progress in applying EIT cooling to a single $^{25}$Mg$^+$ ion, theoretical understanding of limitations of the technique, and extensions to sympathetic cooling of mixed-species crystals. In particular, we show EIT cooling of a 1.2 MHz axial mode of a single $^{25}$Mg$^+$ ion to an average motional occupation number $\bar{n}$ < 0.4 in under 1 ms.

We have also coupled pairs of motional modes of various mixed- and same-species ion crystals using an electric potential that oscillates at the difference of two motional frequencies and has suitable spatial dependence. Mode coupling can be used for increased motional control and can aid in sympathetic cooling and quantum-logic spectroscopy. This coupling can enable certain ions within a mixed-species chain to cool and read out states of motional modes in which the addressed ions' participation is small or zero. We demonstrate this by using $^{25}$Mg$^+$ in a $^9$Be$^+$-$^{25}$Mg$^+$-$^9$Be$^+$ crystal to perform sympathetic cooling and repeated readout of the axial “Stretch” mode in which the center $^{25}$Mg$^+$ ion does not participate.

17:00 Quantum correlated light beams from cascade four-wave mixing in cold atoms

Optical parametric amplifiers are known in the literature as a tool for the generation of quantum correlated beams. Forward four-wave mixing (FWM) with gain factors on the order of 10 associated with strong intensity squeezing [1] is behind, for example, the generation of entangled fields [2].

In this work, we explore both the internal and external atomic degrees of freedom to demonstrate the observation of giant gain and parametric oscillation in multiple FWM processes in a sample of cold cesium atoms. The parametric probe-beam amplification exceeds 2000 and is accompanied by the generation of three other beams of equivalent power emitted along the directions satisfying the phase-matching conditions for multiple cascade forward and backward FWM [3, 4].

The quantum correlations among these fields are investigated by combining in-quadrature electronic local oscillators and heterodyne detection, allowing the measurement of the fields' quadratures and the reconstruction of the covariance matrix.

Also, a full Liouville–Maxwell equations calculation in the extended Hilbert space of the internal and external atomic degrees of freedom allows us to obtain, from first principles, the four-wave propagation equations.

[1] C. F. McCormick, A. M. Marino,V.Boyer, and P. D. Lett, Phys. Rev. A 78, 043816 (2008).
[2] V. Boyer, A. M. Marino, R. C. Pooser, and P. D. Lett, Science 321 321, 544 (2008).
[3] J. P. Lopez, A. J. F. de Almeida, D. Felinto, and J. W. R. Tabosa, Opt. Lett. 42, 4474 (2017).
[4] J. P. Lopez, A. M. G. de Melo, and J. W. R. Tabosa, Opt. Lett. , 45, 3490 (2020).

17:00 Quantum gas microscopy of triangular lattice Mott insulators

Frustrated quantum systems can host quasi-particles with fractional statistics and pose significant challenges to condensed matter theory due to their extensive ground state degeneracy. Here, we aim at quantum simulation of electronic systems on triangular lattice geometries using ultracold atoms in a quantum gas microscope.
We present the site-resolved imaging of fermionic lithium atoms in our novel triangular optical lattice geometry and the realization of Mott insulators in the triangular lattice. Our experiment allows for the preparation of triangular Hubbard systems of several hundred atoms and we image these systems with 98% detection fidelity. We report on our progress in characterizing triangular Hubbard systems using site-resolved density and correlation observables in the experiment and discuss comparisons of experimental data to Numerical Linked Cluster Expansion calculations as well as Quantum Monte Carlo simulations.
Our new experimental platform opens the path for studies of kinetic frustration, searches for spin-liquids and investigations of transport properties in frustrated lattices.

17:00 Quantum state control of optically trapped polyatomic molecules

The degrees of freedom inherent in the structure of polyatomic molecules allow for new applications spanning the fields of quantum simulation and computation, ultracold chemistry, and precision measurements of fundamental physics. For example, the complex rovibrational structure of polyatomic molecules generically gives rise to closely-spaced levels of opposite parity that result in linear Stark shifts at modest electric fields, along with states that have zero first-order electric field sensitivity. Here we present our results on laser cooling of CaOH and optical trapping of CaOH in the vibrational bending mode, which possesses such a parity doublet structure. We present microwave spectroscopy of this state for its potential use in quantum science applications. In addition, we discuss the creation of an optical tweezer array of CaOH molecules. The single particle control lent by this platform will open the door to future efforts studying interactions between molecules in optical traps.

17:00 Reconfiguration algorithms and low-latency feedback control system to prepare large configurations of atoms in two-dimensional arrays of optical traps

We report on the design and characterization of exact and heuristic algorithms to solve atom reconfiguration problems. These algorithms can be used to prepare deterministic configurations of atoms in two-dimensional arrays of optical traps, as well as to realize quantum many-body systems with dynamic connectivity graphs and time-varying interactions. We numerically quantify the operational performance of our algorithms using realistic experimental parameters. Our results indicate that implementing the redistribution-reconfiguration (red-rec) algorithm would enable the assembly of arrays of 256 and 1024 atoms using 512 and 2048 optical traps with a success probability of 91.3(2)$~\%$ and 21(1)$~\%$, respectively. Further rejecting configurations of atoms containing less atoms than a given threshold results in greater mean success probability.

We further report on the design and characterization of a low-latency reconfiguration system to perform feedback control experiments on atomic systems. The system exploits low-latency communication protocols among hardware devices and parallel processing on a CPU or a GPU to speed up the process of acquiring and processing images, generating control sequences, and synthesizing and streaming waveforms actuating active diffractive optical elements. We benchmark and optimize the computational runtime for different reconfiguration problem sizes, identifying the regime for which the GPU outperforms the CPU. This system can readily be deployed for real-time operation to actuate dynamic arrays of optical traps, realizing adaptive, variational, and error correction protocols, as well as synthesizing and streaming optimal control pulses.

17:00 Sagnac atom interferometer gyroscope with large enclosed area and multiple orbits

Sagnac atom interferometers are a promising technique for high-performance rotation sensing, with potential applications for inertial navigation. The use of trapped atoms for the interferometer avoids the need for long free-fall distances that would be incompatible with a navigation apparatus. We have previously demonstrated a dual Sagnac interferometer using Bose-condensed atoms in a time-orbiting potential trap. We report here on improvements to this approach, including a 3-fold increase in the orbit radius and the use of multiple orbits. These improvements lead to an enclosed area of 8.2 mm$^2$, which corresponds to a rotation sensitivity of $6×10^-7$ rad/s at shot-noise-limited detection. While shot-noise-limited performance has not yet be achieved, the interferometer operation is sufficiently stable to permit useful averaging times longer than $10^4$ s. We also discuss a new, more compact, version of the apparatus that is based on an atom chip and which will be suitable for environmental testing.

17:00 Scalable Qubit Arrays for Quantum Computation and Simulation

Quantum computation offers a revolutionary approach to how information is processed, offering new applications in material design, quantum chemistry and speed up of real-world optimisation problems, however a large number of qubits are required to obtain quantum advantage over classical hardware. Neutral atoms are an excellent candidate for practical quantum computing, enabling large numbers of identical qubits to be cooled and trapped, overcoming major barriers to scaling experienced by competing architectures [1]. A crucial ingredient for quantum computing is the ability to perform controlled two-qubit gate operations, for which the strong, long-range dipole-dipole interaction between Rydberg atoms can be exploited to implement deterministic gate operations between atoms within a radius of R < 10 μm.

We present progress towards a new experimental platform for quantum computation at the University of Strathclyde based on reconfigurable atom arrays of Cs atoms, demonstrating loading arrays of > 100 qubits as the first step to creating a scalable architecture for quantum computing. We show high-fidelity control and excitation of single qubits to highly excited Rydberg states and exploit the strong long-range dipole-dipole interactions between Rydberg atoms to generate a 2D array of Bell state pairs. These results pave the way to two qubit and multi-qubit gate operations using twophoton adiabatic rapid passage [2].

This work is supported by the EPSRC Prosperity Partnership with M Squared Lasers, Grant No. EP/T005386/1.

[1] M. Saffman, T. Walker, and K. Mølmer, Rev. Mod. Phys. 82, 2313 (2010).
[2] G. Pelegrí, A.J. Daley, and J.D. Pritchard, High-fidelity multiqubit Rydberg gates via two-photon
adiabatic rapid passage. arXiv:2112.13025 (2021).

17:00 Spin dynamics in optical lattices dominated by superexchange via virtual molecules

Simple, paradigmatic systems are important tools in understanding strongly correlated systems. One such system is the Bose-Hubbard model, which can be realized using atoms in optical lattices with delta-function interactions. We report the first experimental observation of two features of the Bose-Hubbard model: superexchange via virtual molecules in excited bands and off-site contact interactions. Adiabatic sweeps confirm the creation of these excited-band molecules, exemplifying a new kind of Feshbach resonance.

17:00 Spin-wave quantum computing with atoms in a single-mode cavity

We present a method for network-capable quantum computing that relies on holographic spin-wave excitations stored collectively in ensembles of qubits. This construction relies on an orthogonal basis of spin waves in a one-dimensional array and is capable of high-fidelity universal linear controllability using only phase shifts, applied in both momentum and position spaces. Neither single-site addressability nor high single-qubit cooperativity is required, and the spin waves can be read out with high efficiency into a single cavity mode for quantum computing and networking applications. We also propose an experimental implementation using a lambda-scheme in a rubidium-atom system to establish linear quantum processing and calculate the expected experimental operational fidelities due to fundamental and technical errors. In this experimental implementation, we show that efficient methods to achieve linear controllability in both a single-ensemble and dual-ensemble configuration is possible. Finally, we show a potential application of the spin-wave processor for continuous-variable quantum information processing and present a scheme to generate large dual-rail cluster states useful for deterministic computing.

17:00 Stand-alone vacuum cell for compact ultracold quantum technologies

In the drive to develop cold-atom quantum technologies, compact vacuum systems are key to enabling quantum sensing for real world applications. These vacuum systems not only have to be reduced in size, weight, and power compared to their traditional counterparts, but face other challenges. Eliminating active pumping addresses both size and power, but introduces the issue of helium gas permeation as passive vacuum pumping techniques do not remove noble gases. Here we present a centilitre-scale vacuum cell, constructed from low helium permeable materials, with an integrated grating magneto-optical trap optic. A robust cold-atom demonstrator is described, loading 107 s-1 laser-cooled 87Rb, with 12 W of electrical power through a USB battery and optical power delivered by fibre. Under active vacuum pumping, with continuous Rb gas emission, a pressure equilibrium of 10-7 mbar is achieved. With purely passive vacuum pumping the pressure stabilises to 3 x 10-6 mbar with a 17-day time constant, and has been demonstrated to work for two years with only passive vacuum pumping. This research continues to advance and will enable a wide range of cold-atom quantum sensors.
Appl. Phys. Lett. 119, 124002 (2021); doi: 10.1063/5.0061010

17:00 SU(2) hadrons on a quantum computer

We realize, for the first time, a non-Abelian gauge theory with both gauge and matter fields on a quantum computer. This enables the observation of hadrons and the calculation of their associated masses. The SU(2) gauge group considered here represents an important first step towards ultimately studying quantum chromodynamics, the theory that describes the properties of protons, neutrons and other hadrons. Quantum computers are able to create important new opportunities for ongoing essential research on gauge theories by providing simulations that are unattainable on classical computers. Our calculations on an IBM superconducting platform utilize a variational quantum eigensolver to study both meson and baryon states, hadrons which have never been seen in a non-Abelian simulation on a quantum computer. We develop a resource-efficient approach that not only allows the implementation of a full SU(2) gauge theory on present-day quantum hardware, but further lays out the premises for future quantum simulations that will address currently unanswered questions in particle and nuclear physics.

17:00 Thermodynamics in nonequilibrium atom-field interactions

Modern quantum sensors on the basis of ultra-cold atoms allow for an unprecedented experimental accuracy and have shown to be useful in fundamental science and real-world applications alike. With the advent of integration and miniaturization of such systems, the shrinking dimension of the setup leads to an increasing impact of the environment on the atoms’ dynamics.
To name only a few examples, thermal and quantum fluctuations, fluctuating-near-fields in the vicinity of a surface, or decoherence due to system+bath coupling will fundamentally limit the uncertainty of the experiment.

We explore the use of stochastic methods, i.e. the quantum Langevin equation, to describe the fundamental uncertainties in nonequilibrium atom-field interactions. To this end, we determine thermodynamic quantities such as dissipated power or the density matrix of the evolving system which can ultimately lead to a concise quantification of fundamental uncertainties. Our approach can be of use in the design and interpretation of future generations of quantum sensors.

References
D. Reiche, F. Intravaia, and K. Busch, APL Photonics 7, 030902 (2022).

Speaker: Daniel Reiche (Humboldt-Universität zu Berlin)

17:00 Time-delayed optical feedback to a cold atom ensemble

The interaction of quantum systems with themselves has been the subject of extensive theoretical[1] and experimental investigations [2,3]. Here, we present new results on the interaction of an ensemble of cold atoms with a time-delayed version of its own spontaneous emission light.

Experimentally, we form a magneto-optical trap (MOT) of caesium atoms around the waist of an optical nanofibre (diameter ~400 nm). One end of the nanofibre terminates in a single-photon detector module (SPCM) and the other end is connected to a 250 m length of normal optical fibre and terminated with a Fibre Bragg Grating (FBG). After accumulating the desired number of atoms, the MOT trapping beams are turned off, and the ensemble is illuminated with a train of short pulses (pulse duration $\sim$200 ns) of an external pump beam, close to resonance with the $D_2$ transition in caesium and intersecting the optical nanofibre at right angles. We detect the arrival times of the spontaneous emission photons into the optical nanofibre.

We observe photons emitted directly towards the SPCM, but also photons that have been emitted towards the FBG, are reflected back, interact with the atoms again and arrive at the detector after a time delay. The delayed photons are partially absorbed by the MOT atoms, thereby creating a system of atoms interacting with a distant mirror image [3].

We present an investigation into this interaction, changing the pump laser power, polarisation and detuning, as well as the atom number in the MOT. We also investigate the interaction of the spontaneous emission photons with excited atoms by matching the repetition time of the short pulses to the flight time of the photons going to the FBG and back.

[1] Hannes Pichler, Soonwon Choi, Peter Zoller, and Mikhail D. Lukin. Universal photonic quantum computation via time-delayed feedback. Proceedings of the National Academy of Sciences, 114(43):11362–11367, (2017).

[2] Solano, Pablo, et al. "Super-radiance reveals infinite-range dipole interactions through a nanofiber." Nature communications 8.1 (2017): 1-7.

[3] Light interference from single atoms and their mirror images, J. Eschner, Ch. Raab, F. Schmidt-Kaler and R. Blatt, Nature 413, 495 (2001).

17:00 Tomography of a number-resolving detector by reconstruction of an atomic many-body quantum state

A tomography of many-body quantum states of indistinguishable particles is generally performed by global couplings between the involved states and a subsequent counting of the occupation numbers. While precise couplings belong to the standard toolbox, an accurate number counting presents a considerable challenge for both photonic and atomic quantum states. Here we present an application of a number-resolving atom counting for the state reconstruction of an atomic coherent spin state. We generate a coherent spin state by driving a Rabi coupling between the two hyperfine clock states of an ultracold rubidium ensemble. The result is analyzed by a number-resolving fluorescence detection setup. We characterize the fidelity of our detector and show that a negative-valued Wigner function is associated with it. The results offer an exciting perspective for the high-fidelity tomography of entangled states and can be applied for the future demonstration of Heisenberg-limited atom interferometry.

17:00 Towards a cw superradiant laser: Continuous strong coupling and transport of 88Sr atoms in a ring cavity

Superradiant lasers are a promising path towards realizing a narrow-linewidth, high-precision and high-bandwidth active frequency reference [1]. They shift the phase memory from the optical cavity, which is subject to technical and thermal vibration noise, to an ultra-narrow optical atomic transition of an ensemble of cold atoms trapped inside the cavity. Our previous demonstration of pulsed superradiance on the mHz transition in $^{87}$Sr [2,3] achieved a fractional Allan deviation of 6.7·$10^{-16}$ at 1s of averaging. Moving towards continuous-wave superradiance promises to further improve the short-term frequency stability by orders of magnitude. A key challenge in realizing a cw superradiant laser is the continuous supply of cold atoms into a cavity, while staying in the collective strong coupling regime. 
We demonstrate continuous loading of cold $^{88}$Sr atoms into a ring cavity, after several stages of laser cooling and slowing. We characterize controlled transport of the atoms within the ring cavity using an intracavity travelling wave optical lattice, and demonstrate continuous strong collective atom-cavity coupling through continuous measurement of the vacuum Rabi splitting. We further present ongoing work on characterising apparent continuous collective light emission of the atoms on the 7.5kHz transition in $^{88}$Sr.
[1] D. Meiser et al., Phys. Rev. Lett. 102, 163601 (2009).
[2] M. A. Norcia et al., Science Advances 2, e1601231 (2016)
[3] M. A. Norcia et al., PRX 8, 021036 (2018)

17:00 Towards a single-atom array strongly coupled to an optical microcavity for multiparticle entanglement

Photon-mediated interactions between atoms coupled to an optical cavity are emerging as a powerful tool for engineering entangled states and many-body Hamiltonians. However, single-atom addressing and readout is not available in most of these systems.

Leveraging recent development in atom-tweezer arrays, we will present our current effort to combine the strong coupling regime at the single atom level offered by optical fiber Fabry-Perot microcavities with the versatile manipulation and control of single atom enabled by optical tweezers.
We demonstrate Rubidium single-atom trapping in the tweezers, we map the cavity mode by measuring the cavity transmission of a moving single tweezer-trapped atom and we measure single-atom Rabi splitting characteristic of the strong coupling regime. We will also discuss current developments towards multi-tweezers operation and targeting the deterministic loading of the tweezer array in the cavity.

Upon completion, this experimental platform opens up new possibilities for creating, measuring, and utilizing novel types of multi-particle entangled states, such as the generation of spatially delocalized entangled states for multiparameter quantum-enhanced sensing [1].
It opens also the way to new type of quantum simulation where the cavity field creates an effective all-to-all interaction. Such a quantum simulator will allow exploring the transport in disordered spin systems and conductivity in recently discovered, vacuum-enhanced new materials [2, 3, 4] as well as the dynamics of quantum information transport [5].

[1] M. Gessner et al., Phys. Rev. Lett. 121, 130503 (2019)
[2] E. Orgiu et al, Nature Materials 14 , 1123 (2015)
[3] J. Schachenmayer et al, PRL 114, 196403 (2015)
[4] J. Dubail et al., Phys. Rev. A 105, 023714 (2022)
[5] G. Bentsen et al., Phys. Rev. Lett. 123, 130601 (2019)

17:00 Towards Programmable Strontium Atomic Arrays with Holographic Metasurfaces

Optical tweezer arrays combined with the rich internal structure of alkaline earth atoms enable explorations of new quantum systems for quantum optics, quantum simulation, and quantum computing. We report on our progress towards programmable arrays of strontium atoms generated with holographic metasurfaces. Innovations of our setup include: (1) Demonstration of a novel dispenser-based 2D MOT for strontium that provides a high atomic flux while being compact. (2) The development and implementation of holographic metasurfaces for the creation of high quality optical tweezer arrays with arbitrary geometries in 1D, 2D, and 3D. We have thoroughly characterized the light patterns generated by the metasurfaces and find that they efficiently produce high-quality trapping potentials. We have performed the characterization with 520 nm light, which is an unexplored magic wavelength of the strontium intercombination line. Recently, we have created an ultracold strontium gas at 1 $\mu$K via narrow line cooling. In the next step, we will trap strontium in holographic optical tweezer arrays. The scientific goals of this platform are the creation of highly entangled many-body quantum states that display subradiance, as well as applications in quantum simulation and quantum computation.

We acknowledge support from NSF QII-TAQS and NSF Convergence Accelerator. W.Y. acknowledges support from the Croucher Foundation.

17:00 Towards quantum control and spectroscopy of a single hydrogen molecular ion

The complexity and variety of molecules offer opportunities for metrology and quantum information that go beyond what is possible with atomic systems. The hydrogen molecular ion is the simplest of all molecules and can thus be calculated ab initio to very high precision [1]. In combination with spectroscopy this allows to determine fundamental constants and test fundamental theory at record precision [2–4]. Spectroscopy of the hydrogen molecular ion should improve substantially by performing experiments with single hydrogen molecular ions, reducing systematic uncertainties and improving signal strength. This necessitates quantum control.
I will present our progress towards full quantum control of a single hydrogen molecular ion. Our most recent results demonstrate the co-trapping of single H$_2^+$ and $^9$Be$^+$ ions. We observe H$_2^+$ trapping lifetimes of $\approx 10 \mathrm{h}$. We perform ground-state cooling of the ion pair’s axial in-phase mode of motion, resulting in an average phonon number of 0.088(4), which corresponds to a temperature of 24.8(4) μK.
The experimental apparatus features a cryogenic ultra-high vacuum chamber, housing a microfabricated monolithic linear Paul trap. H$_2^+$ is loaded into the trap by electron bombardment of H$_2$. We aim to use He buffer gas cooling in combination with quantum logic spectroscopy to initialize the internal state of H$_2^+$ in a pure quantum state and implement non-destructive readout [5, 6].

[1] V. I. Korobov, J.-P. Karr, M. Haidar, and Z.-X. Zhong, “Hyperfine structure in the H$_2^+$ and HD$^+$ molecular ions at order mα$^6$,”
Phys. Rev. A, vol. 102, p. 022804, Aug 2020.

[2] S. Alighanbari, G. S. Giri, F. L. Constantin, V. I. Korobov, and S. Schiller, “Precise test of quantum electrodynamics and determination of fundamental constants with HD$^+$ ions,”
Nature, vol. 581, no. 7807, pp. 152–158, 2020.

[3] S. Patra, M. Germann, J.-P. Karr, M. Haidar, L. Hilico, V. I. Korobov, F. M. J. Cozijn, K. S. E. Eikema, W. Ubachs, and J. C. J. Koelemeij, “Proton-electron mass ratio from laser spectroscopy of HD$^+$ at the part-per-trillion level,”
Science, vol. 369, no. 6508, pp. 1238–1241, 2020.

[4] I. V. Kortunov, S. Alighanbari, M. G. Hansen, G. S. Giri, V. I. Korobov, and
S. Schiller, “Proton–electron mass ratio by high-resolution optical spectroscopy of ion ensembles in the resolved-carrier regime,”
Nature Physics, vol. 17, pp. 569–573, 2021.

[5] S. Schiller, I. Kortunov, M. Hernández Vera, F. Gianturco, and H. da Silva,
“Quantum state preparation of homonuclear molecular ions enabled via a cold buffer gas: An ab initio study for the H$_2^+$ and the D$_2^+$ case,”
Phys. Rev. A, vol. 95, p. 043411, 2017.

[6] P. O. Schmidt, T. Rosenband, C. Langer, W. M. Itano, J. C. Bergquist, and D. J. Wineland, “Spectroscopy using quantum logic,”
Science, vol. 309, pp. 749–752, 2005.

17:00 Towards relativistic geodesy with a transportable aluminum ion quantum logic optical clock

In relativistic geodesy, frequencies of distant optical clocks are compared to measure the relativistic redshift and thereby the geodetic height difference between the clocks. To obtain a height resolution of on the order of 1 cm, clocks with a fractional frequency uncertainty of 10-18 are required.
Here, we present a joint effort between PTB and DLR-SI to build a transportable aluminum ion clock. In contrast to other species, the aluminum clock transition is very insensitive to blackbody radiation. The linear and quadratic Zeeman shifts are small, and the electric quadrupole shift is negligible. These favorable features led to the first optical clock with an estimated systematic uncertainty below 10-18 [1]. However, a co-trapped so-called logic ion is required for sympathetic cooling and state readout via quantum logic spectroscopy [2].
The transportable clock setup benefits from our experience gained during development of a similar laboratory clock apparatus with a preliminary estimated apparatus-related systematic fractional frequency uncertainty of 1.9x10-18 [3]. Other key-components are a segmented multi-layer trap made of AlN substrates [4], a transportable reference cavity for the clock laser [5], and a single-pass fourth harmonic generation unit for the clock laser that facilitates an uninterrupted phase stabilization of the fundamental laser.
We present preliminary characterization results of the reference cavity and the FHG unit as key building blocks of the clock laser. Moreover, we present potential applications of such clocks for geodetic measurement campaigns.

[1] S. Brewer et al., “27Al+ Quantum-Logic Clock with a Systematic Uncertainty below 10−18” Phys. Rev. Lett. 123 (3 2019), p. 033201
[2] P.O. Schmidt et al., “Spectroscopy Using Quantum Logic.” Science 309.5735 (2005), pp. 749-752
[3] S. Hannig et al. (2019), “Towards a transportable aluminium ion quantum logic optical clock”, Rev. Sci. Instrum. 90, 053204
[4] T. Burgermeister (2019), “Development and characterization of a linear ion trap for an improved optical clock performance”. Phd thesis, Leibniz Universität Hannover.
[5] S. Herbers (2021), “Transportable ultra-stable laser system with an instability down to 10−16“. Phd thesis, Leibniz Universität Hannover.

17:00 Towards the development of an optical lattice clock using bosonic isotopes of mercury

Optical clocks have now reached accuracies close to 1 x $10^{-18}$ [1] [2]. Thanks to their extremely low uncertainties, they are used as tools for various applications, such as chronometric geodesy, tests of General Relativity, search for physics beyond the Standard Model or redefinition of the SI second [3].

Mercury has not been much investigated in cold atoms or quantum gas experiments, and the properties of its various stable isotopes are still to be explored. Moreover, optical lattice clocks based on mercury are studied because of certain advantages over other neutral atoms. In particular, the mercury clock transition$ ^{1}S_0$ - $ ^{3}P_0$ has a low sensitivity to black-body radiation (BBR), that is to say the energy level shift due to the thermal radiation of an environment at a non zero temperature. Its sensitivity to BBR is 16 times lower than ytterbium and 30 times lower than strontium, two of the most successful clock species. It also has a high saturation vapor pressure favorable to implement a 2D magneto-optical trap as an efficient source of pre-cooled atoms. The mercury clock transition has a relatively high sensitivity to a putative variation of the fine structure constant [4], and hence allows to constrain theories aiming to unify gravity with other interactions and to search for dark matter. Working with mercury implies using UV-transitions which is one of the main experimental challenges. Developments of optical lattice clocks using mercury have been focusing so far on the $ ^{199}$Hg fermionic isotope [5][6].

The clock transition$ ^{1}S_0$ - $ ^{3}P_0$ of $ ^{199}$Hg is naturally allowed thanks to the hyperfine mixing due to the 1/2 nuclear spin of $ ^{199}$Hg. But the lifetime of the state $ ^{3}P_0$ is becoming smaller than the longer probing time allowed by the new generation of ultrastable lasers, so it is a limiting factor to fully exploit the potential of these novel technology lasers. Instead in bosonic isotopes with a zero nuclear spin, the $ ^{3}P_0$ state has hypothetically an unlimited lifetime. The $ ^{1}S_0$ - $ ^{3}P_0$ transition can be induced with an external magnetic field by a quenching scheme, and thereby giving the possibility to adapt the strength of this coupling to the probe laser characteristics [7]. $ ^{174}$Yb was studied with this method [8][9]. $ ^{88}$Sr clocks also based on this approach were also studied [10] and have shown promising accuracy [11].

In this poster, we will describe the laser cooling methods used, which open the way to study collisional properties. We will describe the optical lattice clock at SYRTE and we will report the achievement made so far on the $ ^{199}$Hg isotope (stability, accuracy budget, comparisons). We will mention limitations of our current setup and explain the scheme, the expectations and the future steps for making a clock using bosonic isotopes of mercury.

References
[1] W. F. McGrew et al., Nature 564, 87–90 (2018).
[2] A. D. Ludlow et al., Rev. Mod. Phys., 87:637–701, Jun 2015.
[3] S. Bize., C. R. Physique, 20(1):153–168, January 2019.
[4] E. J. Angstmann et al., Physical Review A, 70(1), Jul 2004.
[5] R. Tyumenev et al., New Journal of Physics, 18(11):113002, November 2016.
[6] K. Yamanaka et al., Phys. Rev. Lett., 114:230801, Jun 2015.
[7] A. V. Taichenachev et al., Physical Review Letters, 96(8):083001, March 2006.
[8] Z. W. Barber et al., Phys. Rev. Lett., 100:103002, Mar 2008.
[9] Z. W. Barber et al., Physical Review Letters, 96(8), Mar 2006.
[10] X. Baillard et al., Opt.Lett., 32(13):1812–1814, Jul 2007.
[11] S. Origlia et al., Phys. Rev. A, 98:053443, Nov 2018.

17:00 Two-beam self-oscillating OPM for low-drift high-precision DC magnetometry

Finite-field optical magnetometry offers practical advantages in geophysics, surveying and navigation due to the sensitivity and accuracy achievable with alkali double-resonance techniques. In this sensor scheme, resonant modulation at the Larmor frequency is applied to the alkali spins in order to drive the resonant response and maximise signal contrast [1,2]. Homodyne detection also offers a path to noise reduction in scalable electronic systems. In order to develop operating modes and readout schemes we have built a shielded laboratory magnetometer system using anti-relaxation-coated 133Cs cells [3]. We will run this system as a self-oscillating spin maser as a platform for development of low-drift high-precision DC magnetometry, including study of spin dynamics and limiting noise sources.

We present developments of a two-beam optically pumped alkali magnetometer for investigation of stable Cramer-Rao-lower-bound limited magnetometry, spin-noise limited off-resonant detection of spin maser precession and long-timescale shielded optical magnetometry. We discuss potential future development of this system as a network node for new physics searches [4].

References

[1] I. M. Savukov et al., Phys. Rev, Lett. 95, 063004 (2005)
[2] S. Groeger et al., Eur. Phys. J. D 38, 239-247 (2006)
[3] N. Castagna et al., Appl. Phys. B 96, 763-772 (2009)
[4] S. Afach et al., Phys. Of the Dark Univ. 22, 162-180 (2018)

17:00 Ultracold fermions in optical superlattices

The quantum simulation of Fermi-Hubbard models using ultracold atoms in optical lattices has been essential to deepen our understanding of condensed matter systems. With the precise tunability of the model parameters and the possibility to even change the dimensionality of the systems, it allows to investigate many-body quantum phases. In particular, probing spin correlations has been of interest in understanding high-temperature superconductivity.
      Our experimental setup is based on a three-dimensional optical lattice where a vertical lattice confines the atoms in two-dimensional layers. Recently, the vertical lattice has been extended to a superlattice to implement pairs of layers coupled by interlayer tunneling. To introduce the superlattice capabilities to the two-dimensional layers, we are currently working on the implementation and stabilization of an in-plane superlattice. In the future, we are going to investigate topological systems and transport properties in time-dependent superlattices.

17:00 Update of the JILA Gen. III eEDM Experiment

The Standard Model of particle physics is one of the most successful models that we use to describe the universe, yet it is known to be incomplete. Substantial efforts on the theoretical front introduce new physics through extensions of the Standard Model, and these new physics models make predictions on the value of the electric dipole moment of the electron (eEDM). Measurements of (or improved limit on) the eEDM places constraints on these new theories. The eEDM experiments at JILA take advantage of the long trapping time of ions to tap the long coherence times of the eEDM-sensitive states in our molecular ions of choice: HfF$^+$ and ThF$^+$. The ongoing experiment using HfF$^+$ is an upgraded version of our 2017 experiment [1], using a bigger trap for more ions, amongst other improvements for better statistics. The upcoming experiment using ThF$^+$ has wrapped up spectroscopy of the molecule [2,3,4], and we are now setting up a prototype experiment to demonstrate much longer coherence times than HfF$^+$, promised to us by the eEDM-sensitive ground state in ThF$^+$ [2,4]. Herein, we provide a teaser on the demonstration of long coherence times in ThF$^+$.

[1] W. B. Cairncross, D. N. Gresh, M. Grau, K. C. Cossel, T. S. Roussy, Y. Ni, Y. Zhou, J. Ye, and E. A. Cornell, Precision Measurement of the Electron’s Electric Dipole Moment Using Trapped Molecular Ions, Phys. Rev. Lett. 119, 153001 (2017).
[2] D. N. Gresh, K. C. Cossel, Y. Zhou, J. Ye, and E. A. Cornell, Broadband velocity modulation spectroscopy of ThF+ for use in a measurement of the electron electric dipole moment, J. Mol. Spectrosc. 319, 1 (2016).
[3] Y. Zhou, K. B. Ng, L. Cheng, D. N. Gresh, R. W. Field, J. Ye, and E. A. Cornell, Visible and ultraviolet laser spectroscopy of ThF, J. Mol. Spectrosc. 358, 1 (2019).
[4] K. B. Ng, Y. Zhou, L. Cheng, N. Schlossberger, S. Y. Park, T. S. Roussy, L. Caldwell, Y. Shagam, A. J. Vigil, E. A. Cornell, and J. Ye, Spectroscopy on the electron-electric-dipole-moment–sensitive states of ThF$^+$, Phys. Rev. A 105, 022823

17:00 Violation of the Leggett-Garg inequality for a Bose condensate in a double-well potential

The Leggett-Garg (LG) inequality tells us whether or not the dynamics of the macro- scopic system obeys macrorealism, which consists of the assumptions put forward by Leggett and Garg. Violation of the LG inequality implies either the absence of a realistic description of the system or the impossibility of measuring the system noninvasively. In recent works, the LG inequality is experimentally examined in a superconducting flux qubit.
In our study, we discuss the violation of the LG inequality for a Bose condensate in a double-well potential. For the closed system, we clarify the region of the parameters where the LG inequality is violated. For the open system, coupled to a single bosonic mode, we obtain the collapse and revival of the occupation probabilities of the state in a double-well potential, which recursively violates the LG inequality. Furthermore, we reveal the dependence of the violation of the LG inequality on both the coupling strength and the maximum energy of the bath.

Speaker: Mr Tsubasa Sakamoto (Chuo university)

17:00 Ytterbium nuclear-spin qubits in an optical tweezer array

Optical tweezer arrays of Alkaline earth-like atoms are promising for applications in quantum information and metrology. Here, we describe a tweezer platform for trapping and manipulating arrays of $^{171}$Yb atoms [1]. We demonstrate favorable qubit properties of the nuclear spin $I=1/2$, including seconds-scale coherence times and sub-microsecond single-qubit gates. We further show that single $^{171}$Yb atoms can be loaded with $>90$% efficiency into each tweezer, and we employ Raman sideband cooling to prepare atoms in the motional ground states of the tweezers. Lastly, we present recent progress, utilizing $^3$P$_0$ clock and Rydberg state control, towards the realization of mid-circuit measurement and two-qubit Rydberg gates.

[1] Jenkins, A., Lis, J. W., Senoo, A., McGrew, W. F., and Kaufman, A. M. (2021). Ytterbium nuclear-spin qubits in an optical tweezer array. arXiV:2112.06732

Speaker: Alec Jenkins (JILA, University of Colorado and National Institute of Standards and Technology, and Department of Physics, University of Colorado, Boulder)

Friday 22 July

08:00 → 08:45 Registration / Info Desk open 8:00am - 4:00pm

08:45 → 10:30 Plenary session

10:30 → 11:00 Coffee Break

11:10 → 12:20 Plenary session

12:30 → 14:00 Farewell