Description
The investigation of propagation of pulses in optically dressed media is one of the most basic problems in optics. I will analyze a new superluminal propagation regime in the ladder-type three-level systems near a two-photon resonance where an anomalous dispersion appears accompanied by a small absorption. These conditions are necessary to achieve group velocities greater than the speed of light in a vacuum $(v_g>c)$ or negative $(v_g<0)$. In order to achieve these conditions, previous works exploited population inversion, additional fields, and complicated level configurations. Here, I will demonstrate superluminality can be reached through a relatively simple scenario.
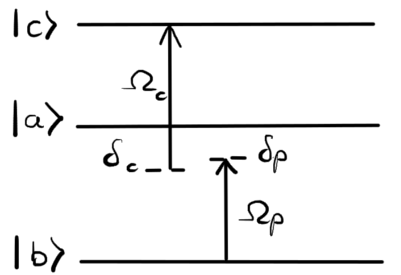
Our model is a one-dimensional medium consisting of three-level systems with the energy levels configuration sketched in Fig. 1. There are electric-dipole-allowed transitions $\vert b \rangle\to \vert a \rangle$ with an energy $\hbar\omega_{ba}$, $\vert a \rangle\to \vert c \rangle$ with an energy $\hbar\omega_{ac}$ and an electric-dipole-forbidden transition $\vert b \rangle\not\to \vert c \rangle$. The lower levels are coupled by the probe field $\Omega_p(z,t)$ (with carrier frequency $\omega_p$), and the upper ones are driven by the control field $\Omega_c(z,t)$ (with carrier frequency $\omega_c$). I will show that to establish the best performance we have to set $\delta_c$ to be hundreds of times greater than the width of the energy levels so we are far from the influence of the single-photon resonance.
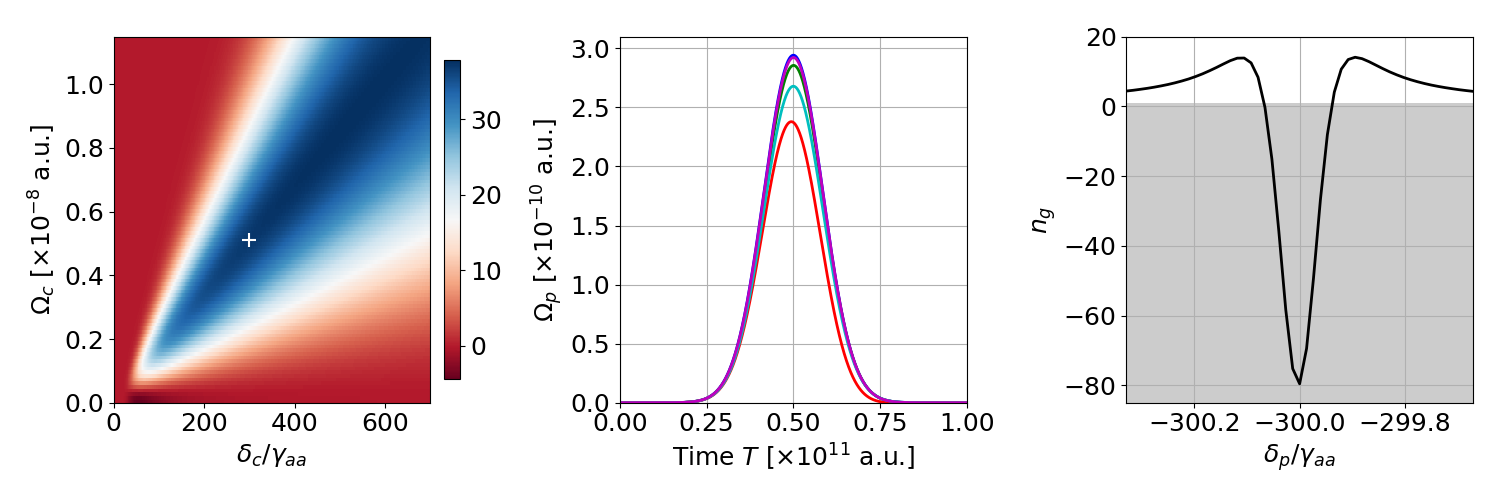
In the numerical simulations, we chose a real-life example of rubidium vapor in a $L=5$ cm long cell well approximated by a one-dimensional model. To optimize the conditions for superluminal propagation in terms of the control field properties $\delta_c$, $\Omega_c$, we introduce the parameter
$\begin{equation*}
%\label{eq:parameter}
\beta(\delta_c, \Omega_c)=\left(1-\min_{\delta_p}(n_g(\delta_p, \delta_c, \Omega_c))\right)\left(e^{-\frac{\omega_{p}}{2c}\chi_{ab}(\delta^\text{min}_p, \delta_c, \Omega_c)L}\right)^4,
\end{equation*}$
where $n_g$ is the group index (related to group velocity by the formula $v_g=c/n_g$) and $\chi_{ab}$ is the electric susceptibility of the medium. The left bracket simply maximizes group velocity in the given conditions while the right one describes absorption. The forth power forces absorption to be no more than 20% to prevent pulse distortions.
As a result, we come up with Fig. 2a where the greater the value of the parameter $\beta$, the better the superluminal conditions. The point for which we analyze the propagation in Fig 2b and 2c is marked with the white plus sign. We consider an input Gaussian pulse with the carrier frequency near two-photon resonance. Fig. 2b shows pulse shapes at the end of the sample for several detunings $\delta_p$ selected to be near two-photon resonance, and indeed, the absorption is limited as expected. Finally, in Fig. 2c, we have group index as a function of detuning $\delta_p$, hence, we have evidence that near the two-photon resonance superluminal propagation occurs as $n_g$ values are well below one (grey region).
In my contribution, I will present a more comprehensive discussion of superluminal propagation regimes.
| Presenter name | Piotr Gładysz |
|---|---|
| How will you attend ICAP-27? | I am planning on in-person attendance |

